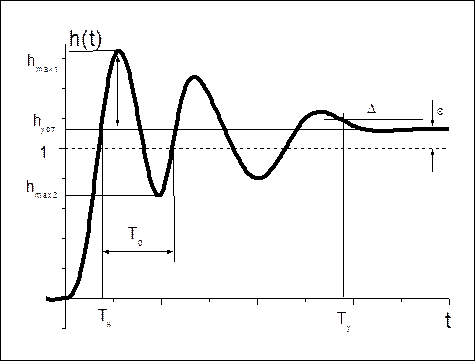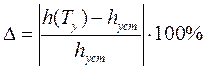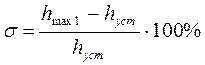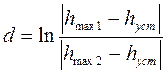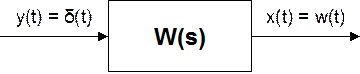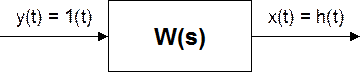Что такое переходная характеристика системы

18.12.202306.07.2022 admin 0 Comments

Переходные характеристики.

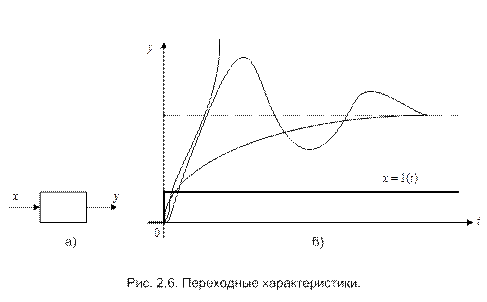
Переходная, или временная, характеристика (функция) звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным. Сказанное иллюстрируется на рис.2.6,а и б. На рис. 2.6,б показаны три различных вида переходных характеристик, соответствующих различным типам звеньев, которые мы рассмотрим далее.

Таким образом, h(t) – это выражение для y(t) при x(t) = 1(t).

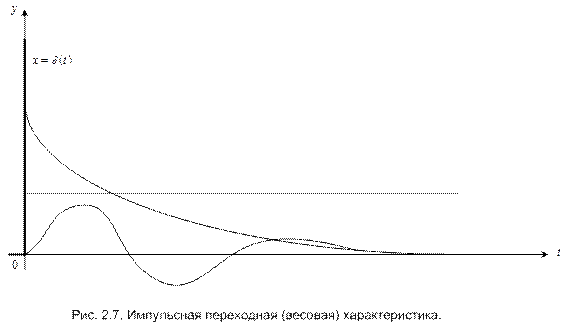
Наряду с переходной характеристикой применяется импульсная переходная (временная)характеристика или функция, называемая еще весовой функцией (функцией веса). Эта характеристика представляет собой реакцию звена на единичный импульс. Единичный импульс (единичная импульсная функция, или дельта-функция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности. На рис.2.4,б он условно показан в виде утолщения на оси ординат. На рис. 2.7 изображены типичные формы самих импульсных переходных характеристик.

Импульсная переходная характеристика обозначается w(t); единичный импульс обозначается δ(t). Таким образом, w(t) – это y(t) при x(t) = δ(t).

При этом, согласно определению,

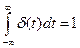
Дельта-функция просто связана с единичной ступенчатой функцией:

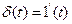
Из этого выражения следует аналогичная связь между переходной и весовой функциями линейных звеньев:

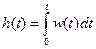
Учитывая это простое соотношение между переходной и весовой функциями, ниже будем применять главным образом первую из них, имея в виду, что вторую при необходимости всегда можно получить дифференцированием по формуле w(t) = h’(t).

Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:

, (2.8)

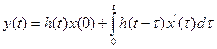
где х(0) – значение х(t) при t = 0;

. (2.9)

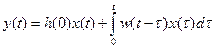
Эти формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки.

Переходные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразования Лапласа над уравнением звена, записанным в общем виде согласно уравнению (2.3,а):

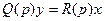
Считая начальные условия нулевыми и учитывая, что обе части этого уравнения представляют собой сумму производных с постоянными коэффициентами, получим:

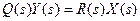
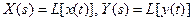
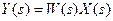
Здесь — изображения Лапласа функций x(t) и y(t); Q(s) и R(s) – полиномы, отличающиеся от исходных полиномов Q(p) и R(p) только заменой оператора дифференцирования р на комплексную переменную s = c + jω. Отсюда

, (2.10)

где 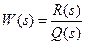— передаточная функция звена (с заменой р на s).

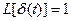
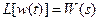
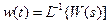
В случае, когда входное воздействие x(t) представляет собой единичный импульс δ(t), учитывая, что его изображение по Лапласу , из (2.10) получаем следующее выражение для изображения весовой функции звена:

, (2.11)

Таким образом, весовая функция определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.

В случае, когда x(t) = 1(t), учитывая, что L[1(t)] = 1/s, из (2.10) получаем выражение для изображения переходной характеристики:

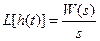
Соответственно переходная характеристика звена

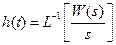
Выражения (2.10) и (2.11) можно трактовать как определения передаточной функции. Согласно (2.10), передаточная функция определяется как отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях. Согласно (2.11), передаточная функция есть изображение Лапласа весовой функции.

Основные параметры переходной функции:

Рис. 2.8. Переходная характеристика САУ.

§ статическое отклонение (статическая ошибка) ε = 1(t) – h_уст. Она характеризует разность между входным и выходным сигналами в установившемся режиме. Системы, у которых статическое отклонение не равно нулю (ε <> 0) называются статическими. Системы, у которых ε = 0, называются астатическими.

§ Динамическое отклонение, т.е. разность между максимальным отклонением и установившемся значением h_max – h_уст.

§ Время регулирования (управления) T_у – это время переходного процесса. Это время, после которого разность между текущим значение выходного сигнала и установившимся значением будет иметь малую величину Δ. Как правило, Δ принимают равным 5% от h_уст.

Время регулирования характеризует быстродействие системы автоматического управления. Чем меньше T_у, тем выше быстродействие.

§ Перерегулирование σ, %. Определяется выражением:

(В реальных системах перерегулирование обычно составляет 10 – 30%).

§ Частота колебаний процесса ω = 2π/T₀, где T₀ – период колебаний.

§ Время нарастания (установления) T_н – время, за которое система достигает установившегося значения.

8.Логарифмические частотные характеристики САУ.

§ Логарифмический декремент затухания, определяется по формуле:

§ Число колебаний n – число максимумов h(t) на промежутке от 0 до T_у.

Функции 1(t) и δ(t) можно использовать для экспериментального определения передаточной функции элемента системы управления:

Первый подход: подадим на вход d * (t). Пусть d*(t) ≈ d(t) (т.к. d(t) физически не реализуема), измерим w * (t) ≈ w(t). Теперь можно вычислить L[w * (t)] = W * (s) ≈ W(s).

Второй подход: На вход подаем 1(t). Измеряем h(t) и вычисляем передаточную функцию. W(s) = L[d/dt(h(t)].

Источник

Переходная характеристика

Переходный процесс — в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы.

Импульсная переходная функция и переходная функция системы включают в себя переходный процесс и установившееся значение при приложении к системе внешнего воздействия в виде дельта-функции и функции Хевисайда соответственно.

Содержание

Характеристики

Важнейшие характеристики переходных процессов переходной функции (реакции системы на единичную функцию):

Перерегулирование

Показывает максимальный «выброс» выходного сигнала системы по амплитуде по отношению к установившемуся значению. Чем больше перерегулирование, тем более система склонна к колебаниям.

Степень затухания переходного процесса

Логарифмический декремент затухания

Время переходного процесса

Время, необходимое выходному сигналу системы для того, чтобы приблизиться к своему установившемуся значению. Обычно пределы такого приближения составляет 1-10 % от конечного значения.

Колебательность

Характеристика системы,которая вычисляется как отношение максимальной амплитуды к установившемуся значению и это отношение умноженное на 100%.выражается в процентах.

Установившаяся ошибка

Установившаяся ошибка системы — разница между предполагаемым и реальным значением выходного сигнала при времени, стремящемся к бесконечности. В идеальных астатических системах установившаяся ошибка равна нулю.

См. также

Полезное

Смотреть что такое «Переходная характеристика» в других словарях:

переходная характеристика — Функция, описывающая изменения в линейной системе (механической, электрической и т.п.), возникающие под влиянием внешнего ступенчатого воздействия, имеющего вид мгновенного скачка от нуля до некоторого постоянного значения, принятого за единицу,… … Справочник технического переводчика

переходная характеристика g(t) — Реакция на прямоугольный импульс, нормированная таким образом, чтобы опорный уровень был равен единице. Примечание Измерительная система может иметь отдельную переходную характеристику для каждого опорного уровня. [МЭК 60 2] Тематики… … Справочник технического переводчика

Переходная характеристика — 1. Переходная характеристика Функция, описывающая изменения в линейной системе (механической, электрической и т.п.), возникающие под влиянием внешнего ступенчатого воздействия, имеющего вид мгновенного скачка от нуля до некоторого постоянного… … Словарь-справочник терминов нормативно-технической документации

переходная характеристика — pereinamojo vyksmo charakteristika statusas T sritis Standartizacija ir metrologija apibrėžtis Elektrinės arba elektroninės grandinės reakcija į vienetinę funkciją. atitikmenys: angl. recovery characteristic; transient characteristic vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

переходная характеристика — pereinamojo vyksmo charakteristika statusas T sritis fizika atitikmenys: angl. recovery characteristic; transient characteristic; transient response vok. Einschwingcharakteristik, f; Einschwingverfahren, n rus. переходная характеристика, f;… … Fizikos terminų žodynas

переходная характеристика — pereinamoji charakteristika statusas T sritis automatika atitikmenys: angl. step response; transfer characteristic; transient response vok. Übergangscharakteristik, f; Übergangskennlinie, f; Sprungantwort, f rus. переходная характеристика, f… … Automatikos terminų žodynas

переходная характеристика — vienetinio šuolio atsakas statusas T sritis radioelektronika atitikmenys: angl. unit step response vok. Einheitssprungantwort, f; Sprungantwort, f rus. переходная характеристика, f; реакция на ступенчатое возмущение, f pranc. réponse indicielle,… … Radioelektronikos terminų žodynas

переходная характеристика — Временная характеристика линейного объекта, находившегося в установившемся режиме функционирования, полученная при единичном скачке входной координаты … Политехнический терминологический толковый словарь

переходная характеристика импульсного фотометра — (h(t)) Характеристика, определяемая реакцией импульсного фотометра на воздействие импульса излучения, имеющего вид единичного скачка. [ГОСТ 24286 88] Тематики оптика, оптические приборы и измерения Обобщающие термины характеристики импульсного… … Справочник технического переводчика

переходная характеристика электронного датчика [преобразователя физической величины] — Динамическая характеристика электронного датчика [преобразователя физической величины], отражающая изменение во времени выходного сигнала при ступенчатом изменении входного сигнала. [ГОСТ Р 51086 97] Тематики датчики и преобразователи физических… … Справочник технического переводчика

Источник

Переходные характеристики

При исследовании систем автоматического управления обычно используются два вида переходных характеристик:

— переходная характеристика, называемая также кривой разгона или временной характеристикой;

— импульсная переходная характеристика, называемая также импульсной характеристикой или функцией веса.

Реакция линейной системы на единичное ступенчатое входное воздействие называется переходной характеристикой – h(t). Эта характеристика может быть получена как аналитически, так и экспериментально путем подачи на вход системы единичного ступенчатого воздействия – x₀(t) и регистрации вызванного этим воздействием значения выхода системы – h(t) (рис. 1 – 12).

Аналитически переходная и импульсная переходная характеристики системы находятся достаточно просто при знании дифференциального уравнения системы. Например, полагая, что дифференциальное уравнение системы имеет вид:

, (1-19)

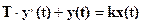
переходная характеристика системы находится как решение этого уравнения при единичном входном воздействии X(t)=I(t) и при начальных условиях Y(t=0)=0. Решение исходного уравнения осуществлялось в § 1-5 и, следовательно, переходная характеристика для рассматриваемой системы имеет вид (рис. 1 – 11):

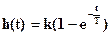
Импульсная переходная характеристика рассматриваемой системы есть решение исходного дифференциального уравнения при

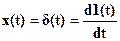
Тогда, так как правая часть есть производная, существующая только в момент времени, равной 0, то при t>0 исходного уравнения – (1-19) соответствует уравнению:

, (1-20)

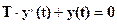
решение которого ищется в виде:

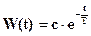
Начальные условия Y(0) находятся путем интегрирования обеих частей уравнения (1-19) в пределах от –t₁ до +t₁

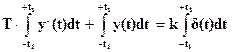
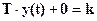
отсюда находим начальное условие:

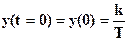
В результате, решения уравнение (1-20) при найденных начальных условиях, записываем импульсную переходную характеристику линейной системы в виде:

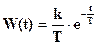
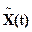
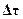
1. Функция — последовательность прямоугольных импульсов длительностью .

2. .

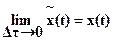
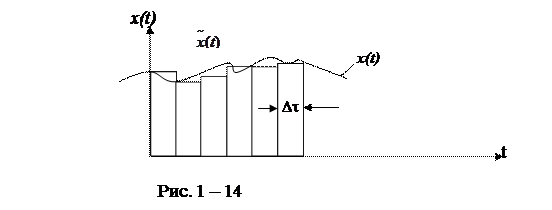
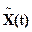
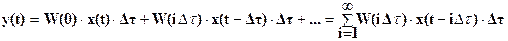
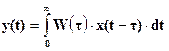
Реакцию системы на достаточно короткий прямоугольный импульс можно считать приближенно равной импульсной переходной характеристике системы W(t), умноженной на площадь этого импульса x(t)×Dt. Следовательно, реакция системы на ступенчатое воздействие будет определяться выражением:

. (1-21)

(1-22)

В результате получается так называемая формула свертки, широко используемая в теории автоматического управления, а операция, осуществляемая этой формулой, называется сверткой функций W(t) и x(t).

Для физически реализуемых систем импульсные переходные характеристики должны удовлетворять условию:

Источник

Переходная характеристика системы

75. Переходная характеристика системы

(для стационарных систем), причем

Смотреть что такое «Переходная характеристика системы» в других словарях:

Переходная характеристика — Переходный процесс в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных… … Википедия

Импульсная переходная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… … Википедия

Переходная функция — Переходная функция в теории управления реакция динамической системы на входное воздействие в виде функции Хевисайда,при нулевых начальных условиях. Зная переходную характеристику, можно определить реакцию системы на произвольное входное… … Википедия

ГОСТ 21878-76: Случайные процессы и динамические системы. Термины и определения — Терминология ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа: Cross power spectral density function of stationary dependent random processes Определения термина из разных документов: Cross power… … Словарь-справочник терминов нормативно-технической документации

Импульсная перезодная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… … Википедия

Импульсная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… … Википедия

ГОСТ 26599-85: Системы передачи волоконно-оптические. Термины и определения — Терминология ГОСТ 26599 85: Системы передачи волоконно оптические. Термины и определения оригинал документа: 84. Акустооптический коммутационный прибор Оптический коммутационный прибор, в котором оптическая коммутация осуществляется за счет… … Словарь-справочник терминов нормативно-технической документации

Импульсная переходная функция — Содержание 1 Определение 2 Свойства 3 Применение … Википедия

Источник

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше: