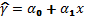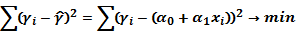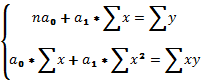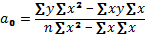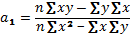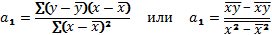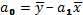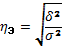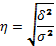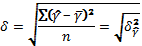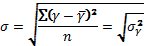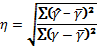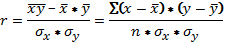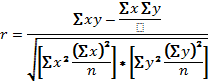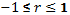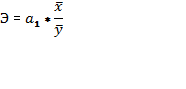Что такое парная корреляция
Парная корреляция и множественная корреляция.
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:
В основу группировки положены два изучаемых во взаимосвязи признака — X и У. Частоты f показывают количество соответствующих сочетаний X и У. Если f.. расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания тц допустимо утверждать о связи между X и У. При этом, если f.. концентрируются около одной из двух диагоналей, имеет место прямая или обратная линейная связь.
Наглядным изображением корреляционной таблицы служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладываются значения X, по оси ординат — У, а точками показывается сочетание X и У. По расположению точек, и* концентрации в определенном направлении можно судить о наличии связи.
В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения — одно по X, другое по У. Рассчитаем для каждого Х; среднее значение У, т. е. У,, как
Последовательность точек (X, У,) дает график, который иллюстрирует зависимость среднего значения результативного признака У от факторного X, — эмпирическую линию регрессии, наглядно показывающую, как изменяется У по мере изменения X.
По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.
Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных X и У, то он вычисляется по формуле
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.
Множественная корреляция
Оценки тесноты связи (корреляции) могут играть двоякую роль. Это — самостоятельные характеристики, дающие представление и о взаимодействии изучаемых факторов, и об аппроксимации фактических данных аналитической функцией. Поэтому расчет показателей множественной корреляции предполагает оценку уравнений регрессии.
При оценке линейной множественной связи рассчитывают коэффициент множественной корреляции. По смыслу он отражает тесноту связи между вариацией зависимой переменной и вариациями всех включенных в анализ независимых переменных. Обычно сначала строится линейная множественная регрессия, а затем оценивается сам коэффициент.
Наиболее общие формулы для его определения имеют следующий вид: 
о2ост —остаточная дисперсия, характеризующая вариацию У за счет факторов, не включенных в уравнение регрессии.
Коэффициент множественной корреляции изменяется от О до 1. Чем ближе R к 1, тем более сильная связь между у и множеством X. Эта же оценка R используется и как мера точности аппроксимации фактических данных выравненным. Если R. незначительно по величине (как правило, R =
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Метод корреляционного анализа: пример. Корреляционный анализ — это…
Понятие о корреляционном анализе
Существует множество определений термина. Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.
Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.
Задачи корреляционного анализа
Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.
Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:
Условия использования метода
Результативные факторы зависят от одного до нескольких факторов. Метод корреляционного анализа может применяться в том случае, если имеется большое количество наблюдений о величине результативных и факторных показателей (факторов), при этом исследуемые факторы должны быть количественными и отражаться в конкретных источниках. Первое может определяться нормальным законом — в этом случае результатом корреляционного анализа выступают коэффициенты корреляции Пирсона, либо, в случае, если признаки не подчиняются этому закону, используется коэффициент ранговой корреляции Спирмена.
Оценка тесноты связи
Теснота корреляционной связи определяется по коэффициенту корреляции (r): сильная — r = ±0,7 до ±1, средняя — r = ±0,3 до ±0,699, слабая — r = 0 до ±0,299. Данная классификация не является строгой. На рисунке показана несколько иная схема.
Правила отбора факторов корреляционного анализа
При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.
Отображение результатов
Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.
Трехмерное представление диаграммы разброса (рассеивания)
Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.
Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.
Ссылки
Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.
Исходные данные для корреляционного анализа
| Профессиональная группа | курение | смертность |
| Фермеры, лесники и рыбаки | 77 | 84 |
| Шахтеры и работники карьеров | 137 | 116 |
| Производители газа, кокса и химических веществ | 117 | 123 |
| Изготовители стекла и керамики | 94 | 128 |
| Работники печей, кузнечных, литейных и прокатных станов | 116 | 155 |
| Работники электротехники и электроники | 102 | 101 |
| Инженерные и смежные профессии | 111 | 118 |
| Деревообрабатывающие производства | 93 | 113 |
| Кожевенники | 88 | 104 |
| Текстильные рабочие | 102 | 88 |
| Изготовители рабочей одежды | 91 | 104 |
| Работники пищевой, питьевой и табачной промышленности | 104 | 129 |
| Производители бумаги и печати | 107 | 86 |
| Производители других продуктов | 112 | 96 |
| Строители | 113 | 144 |
| Художники и декораторы | 110 | 139 |
| Водители стационарных двигателей, кранов и т. д. | 125 | 113 |
| Рабочие, не включенные в другие места | 133 | 146 |
| Работники транспорта и связи | 115 | 128 |
| Складские рабочие, кладовщики, упаковщики и работники разливочных машин | 105 | 115 |
| Канцелярские работники | 87 | 79 |
| Продавцы | 91 | 85 |
| Работники службы спорта и отдыха | 100 | 120 |
| Администраторы и менеджеры | 76 | 60 |
| Профессионалы, технические работники и художники | 66 | 51 |
Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.
С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.
Литература
Использование ПО при проведении корреляционного анализа
Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный анализ в Excel предполагает вычисление следующих параметров с использованием функций:
1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ [CORREL](массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.
Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию ПИРСОН (PEARSON) с теми же массивами.
Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».
После указания исходных данных получаем график.
2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).
3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Парная корреляция



Наиболее разработанной в теории статистики является методология однофакторного корреляционно-регрессионного анализа или парной корреляции, рассматривающей влияние вариации факторного признака x на результативный y.
Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление на основе анализа исходной информации соответствующей математической функции. Сложность заключается а том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляется эмпирическим перебором и оценкой функций различных типов.
При изучении связи экономических показателей используют различные виды уравнения прямолинейной и криволинейных связей, внимание к линейным связям обеспечивается тем, что в большинстве случаев нелинейные формы для выполнения расчетов путем логарифмирования или замены переменных могут быть преобразованы в линейную форму.
Уравнение парной линейной корреляции имеет вид (9.1):
Где 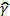
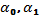
Поскольку 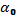
Коэффициент парной линейной регрессииa1 имеет смысл показателя силы связи между вариацией факторного признака x и вариацией результативного признака. Коэффициент показывает среднее значение изменения результативного признака y при изменении факторного признака x на одну единицу его измерения, т.е. вариацию y, приходящуюся на единицу вариации x. Знак a1 указывает направление этого изменения.
Параметры уравнения a0, a1 находятся методом наименьших квадратов, в основу которого положено требование минимальности сумм квадратов отклонений эмпирических данных y1 от теоретических 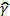
Для нахождения минимума данной функции ее частные производные приравниваются к нулю и решается следующая система нормальных уравнений (9.3):
Решение системы позволяет определить параметры уравнения регрессии. В общем виде параметры определяются следующим образом (9.4):
Параметры уравнения регрессии в ряде случаев удобно вычислять по следующим формулам, дающим тот же результат (9.5) и (9.6):
Рассчитанные таким образом значения a0 и a1 подставляются в уравнения регрессии.
Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ зачастую проводится для небольшой по объему совокупности. Поэтому показатели регрессии и корреляции могут быть искажены действием случайных факторов, и требуется проверка адекватности модели.
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры x характерны для отображения комплекса условий: не являются ли полученные значения параметров результатом, действия случайных причин.
Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определитьтесноту корреляционной связи между переменными x и y. Тесно-корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением 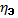
Где 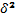
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости от эмпирического корреляционного отношения следует отличать теоретическое. Теоретическое корреляционное отношение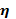
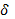
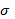
Тогда 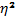
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях стях между результативным и факторным признаками. Теоретическое корреляционное отношение часто называют индексом корреляции R. Корреляционное отношение может находиться в пределах от 0 до 1, т. е. 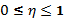
Где n – число наблюдений.
Для практических вычислений при малом числе наблюдений линейный коэффициент корреляции удобнее вычислять по формуле (9.17):
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному и принимает значение в интервале (9.18):
Отрицательные значения указывают на обратную связь, положительные – на прямую. При r=0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее линейная связь между признаками. При 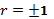
Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками криволинейная. Установлено, что если разность квадратов η 2 и r 2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных величин. Это вызывает необходимость проверки их существенности.
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
При линейной однофакторной связи t-критерий можно рассчитать по формуле (9.19):
гле (n-2) — число степеней свободы при заданном уровне значимости a и объеме выборки n.
После проверки адекватности построенной модели (уравнение регрессии) ее необходимо проанализировать, дать экономическую интерпретацию параметров регрессии. Прежде всего нужно проверить, согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак. Далее необходимо проанализировать значение параметра a1. Очевидно, что для линейной регрессии параметр a1 говорит о том, на сколько абсолютных единиц изменится результативный признак при изменении факторного на 1. Для удобства интерпретации параметра a1 используют коэффициент эластичности. Он показывает, на сколько процентов от его среднего значения изменится результативный признак при изменении факторного признака на 1% от его средней величины, и вычисляется по формуле (9.20):
Далее имеет смысл вычислить остатки 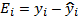
Пример. Методами корреляционного и регрессионного анализа требуется оценить зависимость производительности труда рабочих от стажа их работы по следующим исходным данным.