Что такое параллелограмм и параллелепипед

Параллелепипед

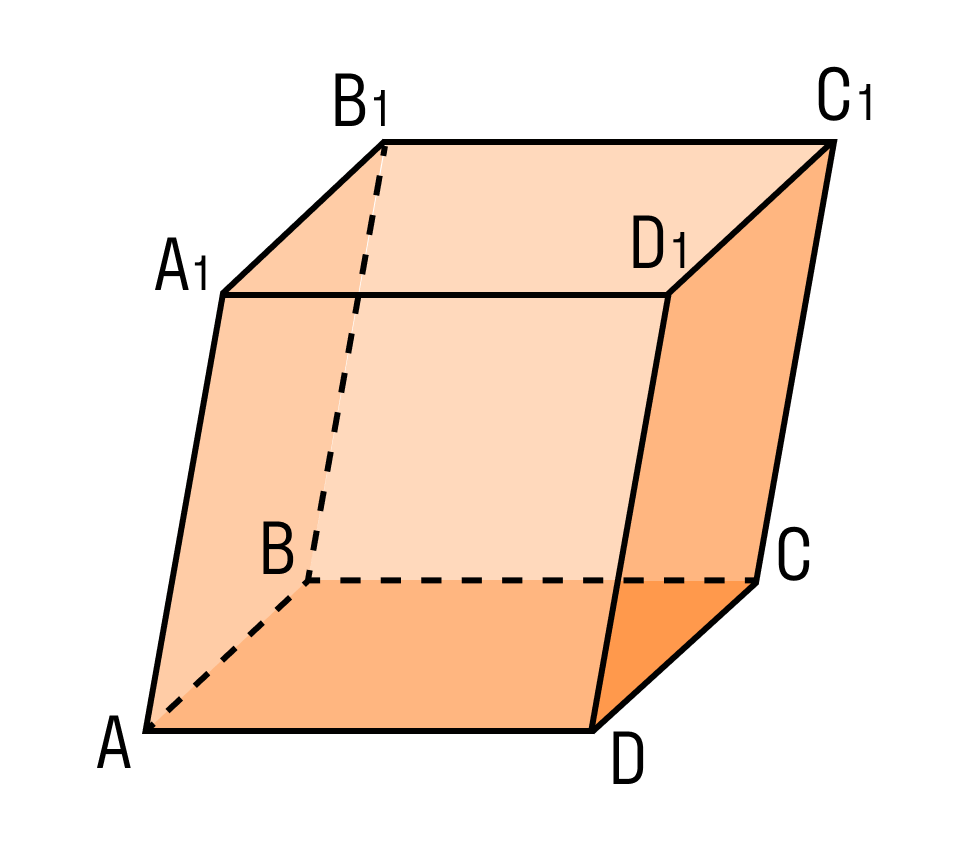
Параллелепипед — тело строгих геометрических форм, противоположные грани которого находятся в параллельных плоскостях. Все плоскости, или грани, включая основание, параллелограммы. Научно определение параллелепипеда — призма, основанием которой служит параллелограмм. Часто ученики затрудняются ответить, чем отличается параллелограмм от параллелепипеда. Отличие в том, что параллелограмм — фигура плоская, двухмерная, а параллелепипед — объемное геометрическое тело, протяженное в трех измерениях, имеющее ширину, высоту и длину. Как выглядит параллелепипед, посмотрите на рисунке:

Виды параллелепипеда

Параллелепипед — многогранник. Его ограничивают шесть плоскостей, два основания, и четыре боковые грани. Линии, по которым соединяются грани, называются ребрами, а точки, в которых сходятся три ребра — вершинами. У фигуры 8 вершин.

Если грани имеют общее ребро, то их называют смежными, а те, у которых такого ребра нет — противоположными. Это же касается и вершин, если они не лежат на одной грани, то их тоже называют противоположными. Высота, ширина и длина прямоугольного параллелепипеда называются измерениями, они выходят из одной вершины. Если фигура не прямоугольная, то измерения и ребра не совпадают.

При построении параллелепипеда на рисунке можно провести ряд дополнительных линий, которые помогают при вычислении объема, площади поверхности, неизвестных длин и других параметров. Если линии проходят через противоположные вершины, то их называют диагоналями. У параллелепипеда их насчитывается четыре.

В геометрии выделяют несколько типов параллелепипедов, которые отличаются некоторыми свойствами:

Свойства параллелепипеда

Для всех типов параллелепипедов можно выделить общие свойства, характеризующие фигуру. Таких свойств немного, запомнить их не сложно:

Твердо запомнив эти свойства несложно решить большинство задач школьной геометрии.

Основные формулы параллелепипеда

Кроме свойств этой фигуры нужно запомнить ряд несложных формул. Конечно, в процессе решения задачи можно вывести эти выражения самостоятельно. Но часто на это нет времени, лучше воспользоваться готовыми шаблонами.

Формула площади боковой поверхности прямого параллелепипеда — одна из самых простых. S_б=Р_о∙h. В этой формуле только три величины, но одна из них составная:

H – высота параллелепипеда;

Р – периметр, АВ+ВС+АD+ CD.

Воспользоваться такой формулой можно только в том случае, если известны длины сторон основы и высота.

Площадь полной поверхности параллелепипеда определяется по формуле S_п=S_б+2S_о.

Как найти площадь боковой поверхности мы знаем из предыдущего пункта, а площадь S_о рассчитывается в зависимости от вида четырехугольника, лежащего в основании.

Объем прямого параллелепипеда тоже найти несложно, для этого достаточно умножить площадь основания на высоту. Объём V=S_о∙h

Формулы для прямоугольного параллелепипеда тоже не отличаются сложностью:

S_б=2c(a+b) в этой формуле а и b – стороны основания, с – высота, равна длине бокового ребра.

Площадь полной поверхности равна S_п=2(ab+bc+ac);

Объем V=abc, то есть, произведение всех трех измерений.

Когда же приходится вычислять площади и объем произвольного параллелепипеда, то показанные формулы не всегда срабатывают. Необходимо использовать законы векторной геометрии. При вычислении объема параллелепипеда через длину диагонали, необходимо использовать проекции на разные оси. Видимая простота формул — это только основа для сложной работы, требующей пространственного воображения и смекалки.

Источник

Прямоугольный параллелепипед. Что это такое?

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

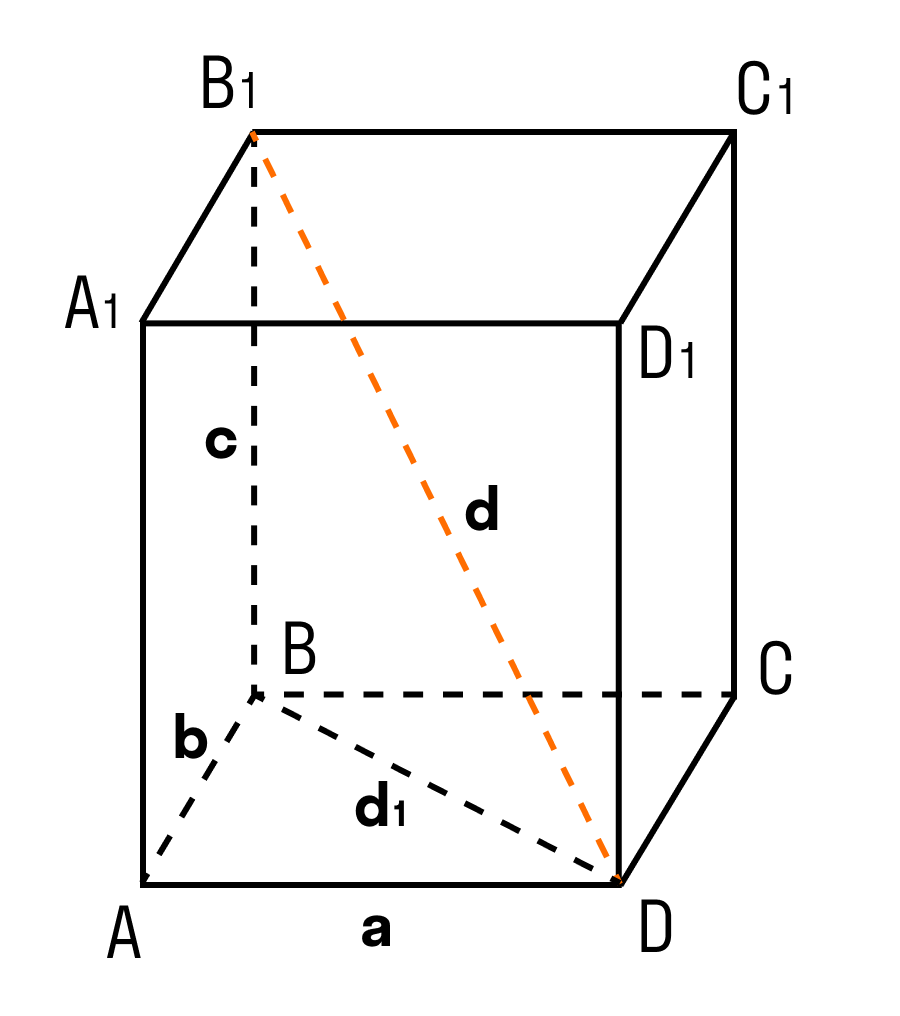
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

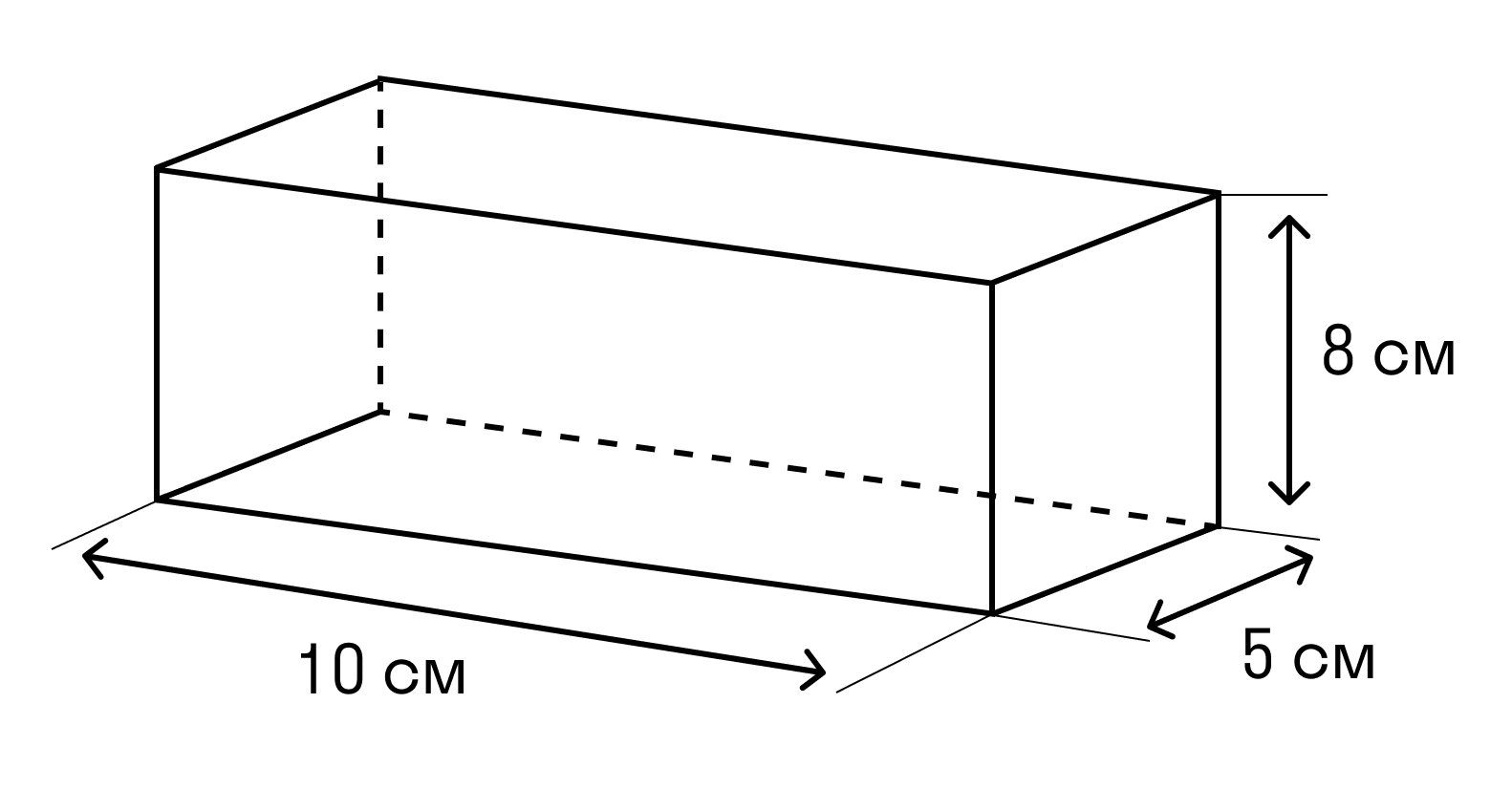
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

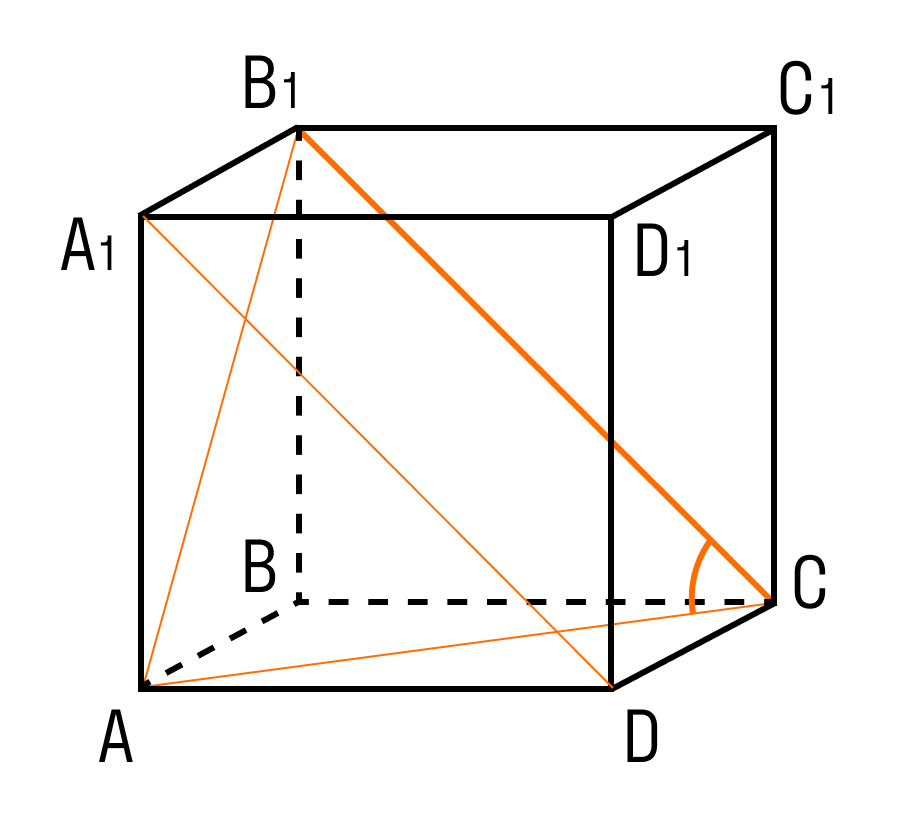
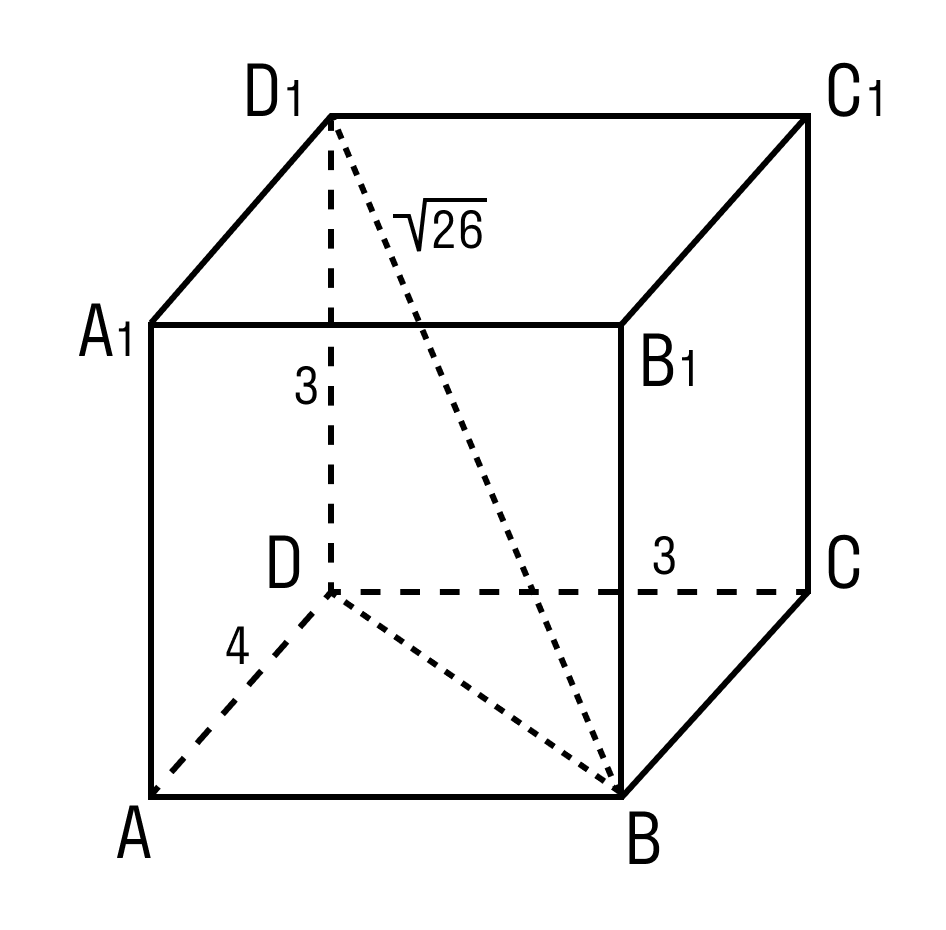
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

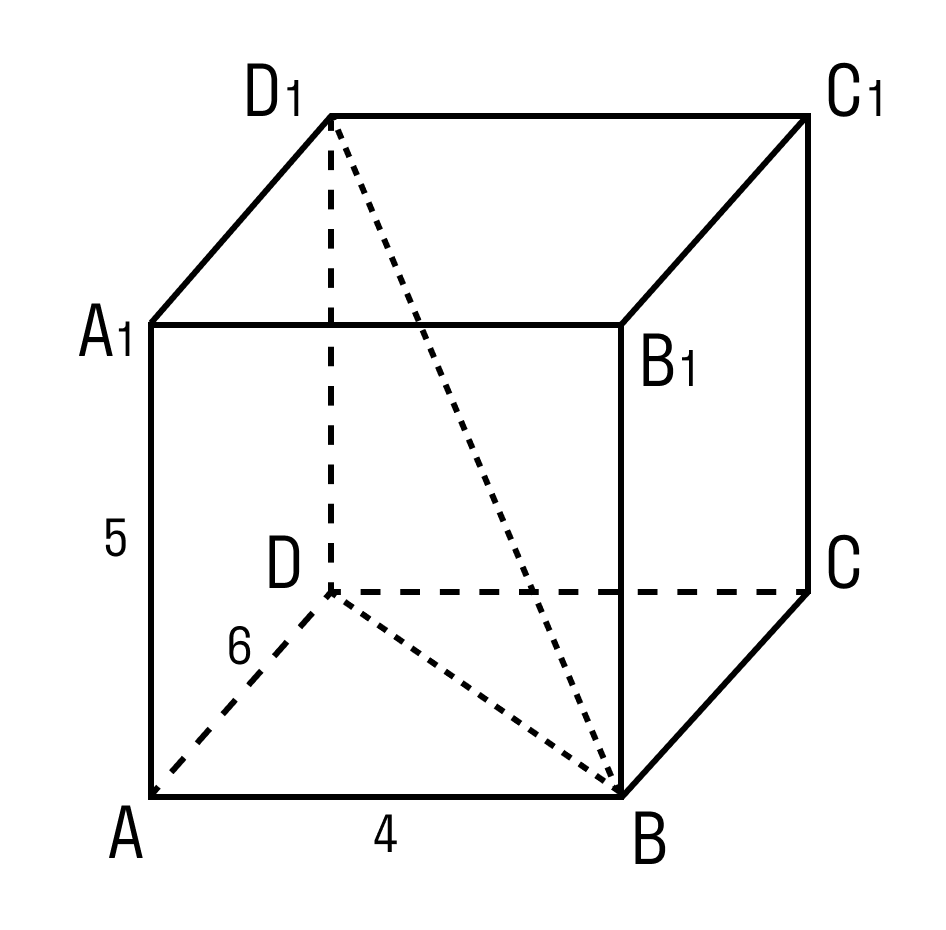
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

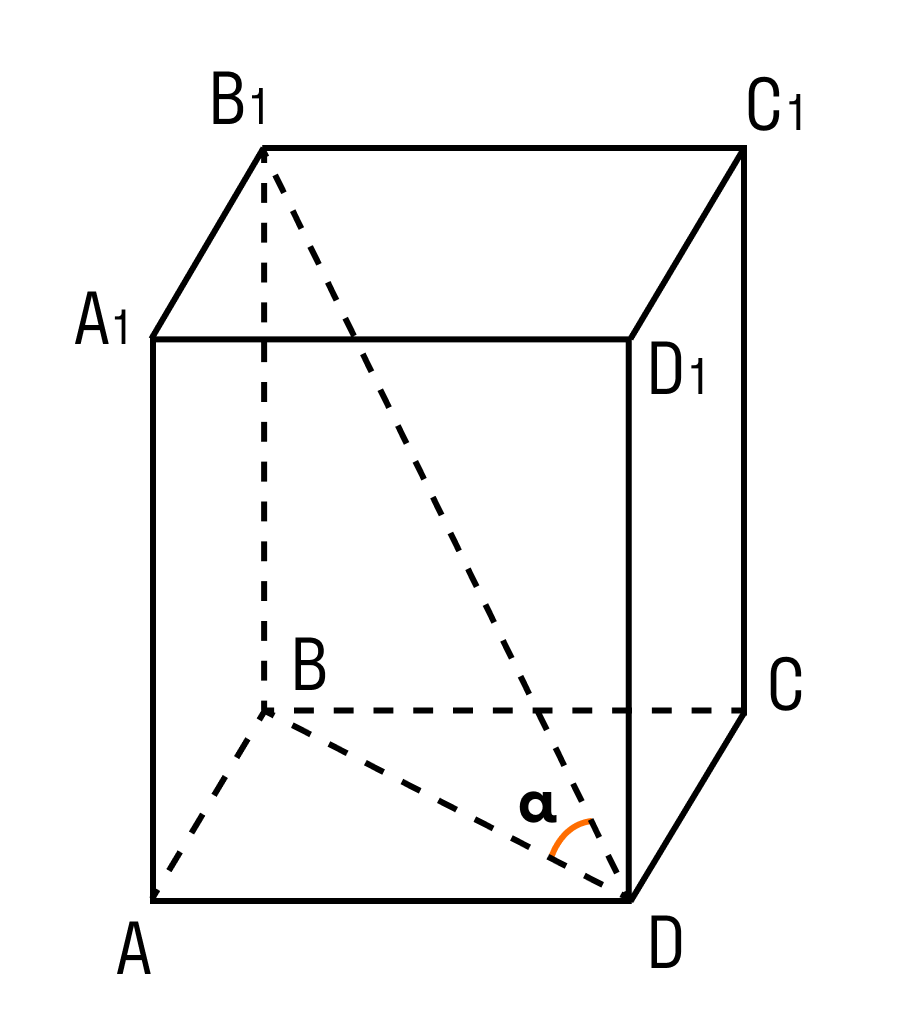
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №7. Тетраэдр и параллелепипед

Перечень вопросов, рассматриваемых в теме

Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.

Сечением поверхности геометрических тел называется – плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Учебник Геометрия 10-11 кл.– М.: Просвещение, 2014.

Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.

Открытый электронный ресурс:

Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru

Теоретический материал для самостоятельного изучения

В дельнейшем несколько уроков нашего курса будет посвящены многогранникам- поверхностям геометрических тел, составленным из многоугольников. Но до более подробного изучения многогранников мы познакомимся с двумя из них- тетраэдром и параллелепипедом. Нам данные тела дадут возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей.

Давайте вспомним, что мы понимали под многоугольником в планиметрии. Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, либо как часть плоскости, ограниченную этой линией, включая ее саму.

Мы будем использовать второе толкование многоугольника при рассмотрении поверхностей и тел в пространстве. При таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.

Давайте рассмотрим изображенную фигуру и ответим на несколько вопросов.

Итак, поверхность данной фигуры состоит из четырёх треугольников DАВ, DВС, DАС и АВС.

Мы с вами выяснили из элементов состоит наша фигура тетраэдр. Теперь сформулируем определение.

Определение. Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Говорят, что рёбра АD и ВС, АВ и CD, и т.д.- противоположные.

Изображается тетраэдр обычно так (рис. 1).

Рисунок 1 – изображение тетраэдра.

Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. И тетраэдр тому доказательство. Так же мы можем наблюдать тетраэдр в повседневной жизни (рис. 2).

Форма пакета молока

Прежде чем начать изучать параллелепипед вспомним определение параллелограмма и его свойства.

Определение. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом (рис. 3).

Рисунок 3 – параллелограмм

1. Противоположные стороны параллелограмма равны:

2. Противоположные углы параллелограмма равны:

3. Диагонали параллелограмма точкой пересечения делятся пополам:

треугольники ABC и CDA равны.

6. Накрест лежащие углы при диагонали равны:

А теперь перейдем к параллелепипеду.

Рассмотрим два равных параллелограмма ABCD и A₁B₁C₁D₁, расположенных в параллельных плоскостях так, что отрезки AA_1, BB_1, CC₁ и DD₁ параллельны.

Давайте рассмотрим изображенную фигуру (рис. 4).

Рисунок 4 – параллелепипед и его диагонали

АВСDA₁B₁C₁D₁: поверхность, составленная из двух равных параллелограммов АВСD и A₁B₁C₁D₁, лежащих в параллельных плоскостях и четырёх параллелограммов.

Определение. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда:
A₁C, D₁B, AC₁, DB₁.

Параллелепипед – слово греческого происхождения, параллел – идущий рядом, епипед – плоскость.

Определение.Параллелепипед- этошестигранник с параллельными и равными противоположными гранями.

Следует отметить, что многоугольник в пространстве представляет собой плоскую поверхность, а тетраэдр и параллелепипед – поверхности, составленные из плоских поверхностей (соответственно треугольников и параллелограммов).

Способы изображения параллелепипеда

Параллелепипед, в основании которого лежит ромб

Параллелепипед, в основании которого лежит квадрат

Параллелепипед,в основании которого лежит прямоугольник или параллелограмм

Параллелепипед, у которого все грани — равные квадраты

Можно сделать вывод, что параллелепипеды делятся на (рис. 5)

Рисунок 5 – виды параллелепипедов

В параллелепипеде ABCDA₁B₁C₁D₁грани ВВ₁С₁С и AA₁D₁D параллельны (рис. 6), потому что две пересекающиеся прямые ВВ₁ и В₁С₁ одной грани параллельны двум пересекающимся прямым АА₁ и A₁D₁ другой; эти грани и равны, так как В₁С₁ = A₁D₁, В₁В= А₁А (как противоположные стороны параллелограммов) и ∟ ВВ₁С₁= ∟АA₁D₁.

Рисунок 6 – чертеж к доказательству свойства 1

Возьмём какие-нибудь две диагонали, например АС₁ и ВD₁, и проведём вспомогательные прямые АD₁ и ВС₁ (рис. 7).

Так как рёбра АВ и D₁С₁ соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD₁С₁В есть параллелограмм, в котором прямые С₁А и ВD₁ —диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам.

Возьмём теперь одну из этих диагоналей, например АС₁, с третьей диагональю, положим, с В₁D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B₁D и АС₁ и диагонали АС₁ и BD₁(которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали
АС₁. Наконец, взяв эту же диагональ АС₁ с четвёртой диагональю А₁С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС₁. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.

Рисунок 7 – чертеж к доказательству свойства 2

Задачи на построение сечений.

Взаимное расположение многогранника и секущей плоскости:

Фигуры, которые получаются в результате сечения:

Один из методов построения сечений, который мы рассмотрим- метод следа.

Рассмотрим метод следов, применяемый при построении сечений многогранников, а именно при построении сечения куба плоскостью.

Что такое метод следов? При построении сечений многогранников в качестве вспомогательной прямой часто используется след секущей плоскости (в плоскости грани, удобной для рассмотрения). Такой метод построения сечений называется методом следа.

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (рис. 8).

Рисунок 8 –чертеж к задаче №1

Основные правила построения сечений методом следа:

То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.

Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.

Рисунок 9 – чертеж к задаче №2

Решение:
Для решения построим вспомогательную плоскость DМN (рис. 10). Пусть прямая DМ пересекает прямую АВ в точке К. Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.

Примеры и разбор решения заданий тренировочного модуля

Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.

Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС (рис. 11). В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.

Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р₁ и Р₂. Соединяем Р₁ и М и на продолжении получаем точку М₁. Соединяем точку Р₂ и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.

Рисунок 10 – чертеж к примеру 1 (первый случай)

Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС (рис. 12). Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р₁Р₂, тогда прямая Р₁Р₂ параллельна данной прямой MN.

Рисунок 11 – чертеж к примеру 1 (второй случай)

Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым.

Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N (рис. 13).
По теореме (о параллельных прямых) линия пересечения параллельна SB.
В плоскость SBC через т. N проходит NQ||SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. M (прямая MP). По теореме (о параллельных прямых) линия пересечения параллельна SB.

следовательно, PM||NQ.Утверждение доказано.

Источник