Что такое отрезок в математике 2 класс
Что такое отрезок
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.
Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.
Отрезок — это геометрическая фигура
Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.
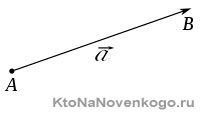
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.
В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.
Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.
Разница между отрезком, лучом и прямой
Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:
Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.
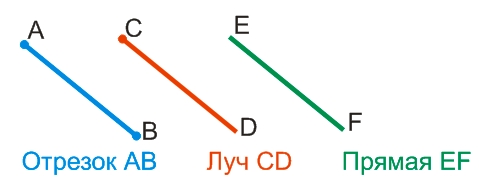
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Направленный отрезок — это вектор
Отрезки бывают двух видов:
Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.
Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ ➜ и ВА ➜ — разные отрезки, так как они противоположно направленные.
Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.
Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.
Ломаная линия — это множество соединенных отрезков
Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.
Вершинами ломаной являются следующие точки:
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
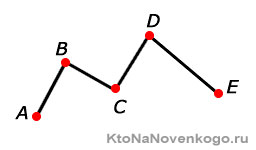
Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.
Любая замкнутая ломаная является геометрической фигурой — многоугольником.
Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.
Отрезок времени
Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.
Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.
Время в целом в таком случае определяется как временная прямая.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Чтобы не путать с лучом, надо просто запомнить, что отрезок — это две точки. То есть эта прямая и на ней две точки — это и называется отрезком.
Это самая простая часть геометрии и надо просто внимательно читать.
Жизнь тоже можно разделить на отрезки и все они будут неотделимо связаны с временем и конкретным человеком.
Основы геометрии
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: « (·) A » — точка « А ».
Прямая
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Способы обозначения прямых
Способы обозначения лучей
Отрезок
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.
Класс: 2
Презентация к уроку
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Слайд 3. Решив данные примеры и расположив ответы в порядке возрастания, вы узнаете, в чье королевство мы сегодня отправимся за новыми знаниями.
Появляется слово «Точка». «Молодцы!» (Слайд 4)
III. Работа над темой урока. Сказка про Точку.
Слово учителя: Сегодня мы отправимся в увлекательное путешествие по стране Геометрии. Встречает нас здесь королева этой страны, без которой невозможно построить ни одной фигуры, это Точка (Слайд 5).
Жила-была Точка. Она была очень любопытна и хотела все знать. Увидит незнакомую линию и непременно спросит:
— Как эта линия называется?
— Длинная она или короткая?
Подумала однажды Точка: «Как же я смогу все узнать, если всегда буду жить на одном месте? «Отправлюсь-ка я в путешествие!».
— Ребята, вы готовы совершить путешествие вместе с Точкой? (Да).
— Ребята, а скоро ли конец прямой? (У прямой нет конца).
— Ребята, сможет ли Точка найти концы прямой? (Нет)
— Опечалилась Точка. Что же, так мне и придется идти, идти и идти без конца?
— А что если я позову на помощь Ножницы?
Тут откуда не возьмись, появились Ножницы. Щелкнули перед самым Точкиным носом и разрезали прямую (Слайд 8)
— Ура! Воскликнула Точка. Получился конец, да не один, а целых два, с одной стороны и с другой! Что же стало с моей прямой? (Слайд 9) Как называется получившаяся фигура? (Отрезок). Чем отличается от прямой? (Имеет начало и конец).
— А я знаю почему они так называются. Воскликнула Точка. Они похожи на солнечные лучики! Солнечные лучи начинаются на солнце и идут от солнца без конца. В Геометрии каждый луч, отрезок, прямая имеют название. Обратите внимание, что луч обозначается либо одной строчной буквой, либо двумя прописными, причем при чтении и записи на первом месте указывается начало луча, а при названии прямой или отрезка порядок не имеет значения. Точка обозначается одной буквой. Давайте правильно прочитаем название фигур (Буквы латинского алфавита). Слайд 11
— В чем отличие прямой от луча? Отрезок от прямой? Луч от отрезка?
Слайд 13. Физминутка. Учащиеся танцуют под «Танец маленьких утят».
IV. Закрепление пройденного материала.
Работа по учебнику Л.Г.Петерсон Математика 2 класс. Тема: «Луч. Отрезок. Прямая».
№ 1. Откройте тетради. Обозначьте точку. Сколько можно провести прямых через данную точку? (Слайд 14) Какой можно сделать вывод? Вывод: через одну точку можно провести сколько угодно прямых.
№ 2. Поставьте две точки на расстоянии друг от друга (Слайд 15). Сколько можно провести прямых через эти две точки? Вывод: Через две точки можно провести только одну прямую.
V. Итоги урока.
2. Что вы узнали о каждой из этих фигур? (Слайд 17)
НУ ВОТ И ВСЕ, КОНЕЦ! А КТО СЛУШАЛ, МОЛОДЕЦ.
Урок–путешествие по математике «Луч. Отрезок. Прямая»
Цель:
Оборудование. Учебник «Математика», 2-й класс (1–4), часть 2 (авт. Л.Г.Петерсон. – М.: Ювента, 2002. – 96 с.: ил); матросские шапки (сделанные детьми); иллюстрация «Море»; цветные карандаши; три клубка ниток; ножницы; банка с водой и «веревочная лестница»; мультимедийное сопровождение (предметные картинки: осьминог, акула, дельфин, кит, корабль).
Ход урока
1. Организационный момент.
2. Постановка темы урока.
Учитель. Сегодня на уроке, мои дорогие мальчики и девочки мы отправимся в уникательное путешествие за новыми знаниями, которые нам предстоит открыть самим. А на каком транспорте мы отправимся, вы узнаете из загадки.
Паровоз без колёс!
Вот так чудо-паровоз
Не с ума ли он сошел
Прямо по морю пошел.
У. На чём же мы отравимся в путешествие?
Дети. На корабле.
У. Да, мы отправимся в путь, вот по этому морю, вот на таком корабле.
На уроке за работу вы будете получать вот такие ракушки, по которым вы получите оценку. (У каждого ребёнка на парте лежат ракушки, которые он будет откладывать за каждый правильный ответ).
(Показ модели корабля и иллюстрации «Море»)
У. Что вы видите?
Д. На доске мы видим 3 линии.
У. С какой из трех линий вы уже знакомы?
Д. Со второй линией.
У. Что предстоит нам узнать?
Д. Как называются 1-я и 3-я линии и познакомимся с их свойствами.
У. Цель ясна! Мы на корабле.
Итак, в путь! Наденьте матроски.
(Дети надевают матросские шапки).
У. На корабле вы матросы, а я ваш капитан.
Но что такое? Наш корабль не заводится. А чтобы он завелся нам нужно заполнить судовой журнал, т.е. тетрадь, в которой вы будете вести все необходимые записи.
Откроем судовой журнал и запишем число и месяц, когда мы отправляемся путешествовать.
(Дети записывают число)
3. Чистописание.
У. 657 – расскажите все об этом числе.
Д. (Ответы детей).
У. Что записано во второй строчке?
Д. Трёхзначные числа.
У. Что нужно найти?
Д. Закономерность.
У. Найдите закономерность и запишите следующие 3 числа.
У. Молодцы ребята. Наш корабль заводится.
4. Решение задачи на смекалку.
У. Итак, наше путешествие начинается.
Наш парус ветер подгоняет
Корабль скользит по ласковой волне
Вон за бортом дельфин играет
Резвязь в прозрачной глубине.
Но что такое? К нам подплывают дельфины. (рис. Дельфин).
Ребята! Дельфины нам сообщает, что около острова к которому мы подплываем ждет огромный осьминог. Он не подпустит нас к острову, если мы не решим его задачу на смекалку. (рис. Осьминог).
Океан спокоен. Идет прилив. Он каждый час поднимает воду на 15 см.
Через сколько времени окажутся в воде три ступеньки веревочной лестницы.
(Обсуждение в группе).
Д. Ответы детей.
У. Берёт банку с водой. Опускает «верёвочную лестницу». (Ответ: нисколько, т.к. с водой поднимается корабль, а с ним и верёвочная лестница).
5. Физкультминутка.
У. Ну что можно смело отправляться в путь. Я вижу, что к нам подплывает рыбка. Она предлагает нам отдохнуть.
(Заранее подготовленный ученик, переодетый в рыбку, проводит физкультминутку).
Рыбки весело резвятся,
В чистой тепленькой в воде.
То сожмутся, разожмутся,
То зароются в песке.
6. Знакомство с новым материалом. Практическая работа.
У. Наше путешествие продолжается. Мы подплываем к острову, где живет огромный осьминог. К острову он нас подпустил, но нам нужно высадиться на него и открыть клад с новыми знаниями. Зачем мы и отправились.
У. Внимание на доску.
а) Вы уже сказали, что знакомы со второй линией, которая называется …
Д. Отрезком.
У. Что знаете об отрезке?
Работа в четверках:
Д. Есть начало и есть конец.
У. Могу ли я отрезок продолжить вправо? Влево?
Д. Нет.
У. Возьмите клубок и ножницы и отрежьте отрезок от нити.
Д. (Дети выполняют практическую работу).
Вывод: Отрезок имеет начало и конец.
У. А как же называется первая линия? Откройте учебник на странице 7 и найдите № 1.
Д. Пряма линия.
У. Посмотрите на прямую внимательно. Что вы заметили?
Д. Нет начала и нет конца.
У. Возьмите двойной клубок. Могу ли я прямую продолжить вправо? Влево?
Д. Да. (Дети выполняют практическую работу).
У. До каких пор? (До бесконечности).
Вывод: Прямая – не имеет ни начала ни конца, ее концы можно продолжать до бесконечности.
У. А сейчас давайте пронаблюдаем за третьей линией, которая называется …
Д. Луч.
У. Что заметили?
Д. Есть начало, но нет конца.
У. Могу ли я начало луча продолжить?
Д. Нет
У. Могу ли продолжить конец луча?
Д. Да.
У. Возьмите ножницы, разрежьте двойной клубок.
Д. (Дети выполняют практическую работу).
У. Сколько лучей получилось?
Д. Два.
У. Что мы можем сделать?
Д. Конец луча продолжить до бесконечности.
Вывод: Луч – это часть прямой, который имеет начало, но не имеет конца.
У. Молодцы! Осьминог вами доволен. Посмотрите как он улыбается всем.
Но к острову подплывает акула. Она не даст нам отплыть от острова, если мы не выполним её творческого задания. (рис. акула).
7. Творческое задание по рядам.
У. Начертите:
1-й ряд – прямую;
2-й ряд – отрезок;
3-й ряд – луч;
поставьте на прямую, отрезок, луч 2 точки. Что же у вас получилось?
Работа в паре.
1-й ряд – отрезок и 4 луча.
2-й ряд – 5 отрезков.
3-й ряд – 3 отрезка и 3 луча.
У. Акула за вас очень рада. Она отплывает. А мы смело можем отправляться обратно.
8. Закрепление нового материала.
Пусть бушуют волны крутые
В лохматых тучах небосвод
Не страшны нам штормы седые
Плывем мы вперед и вперед:
Ребята! Надвигается шторм! По левому борту большой кит. (рис. кит).
9. Д. Игра: Море волнуется.
У. Чтобы море успокоилось нужно выполнить задание кита. Решить задания из учебника.
Задание на стр. 7 № 2, 3.
Проверка по ключу. Кит доволен вами и желает вам счастливого плавания.
10. Итог урока.
У. Слышите! Шторм стихает. И наше путешествие подходит к концу.
Мы подплываем к последнему пункту – к Земле, где нам предстоит высадиться, но высадиться тот, кто сможет продолжить мою мысль, он и высаживается с корабля.
(Ученики ответившие верно снимают матроску).
У. Линия которая имеет:
11. Домашнее задание.
По учебнику стр. 7 № 5.
12. Оценивание.
Молодцы все! Но лучшие матросы встаньте, которые заработали самое большое количества ракушек. Вы получаете оценку «5».
Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
Провести «настоящую» прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
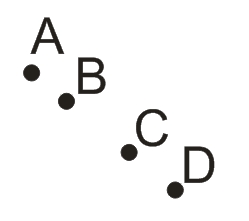
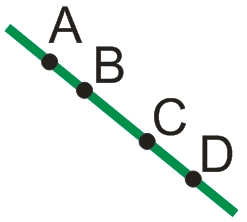
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Доказать это очень просто.
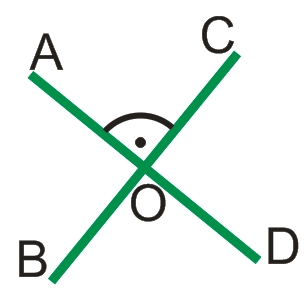
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе