Что такое отношение на множестве
Понятие отношения на множестве
Лекция 20. Отношения на множестве
1. Отношения на множестве. Бинарные отношения.
2. Свойства отношений
§10. ОТНОШЕНИЯ НА МНОЖЕСТВЕ
В математике изучают не только связи между элементами двух множеств, т.е. соответствия, но и связи между элементами одного множества. Называют их отношениями.
Изучение отношений между объектами важно для познания как самих объектов, так и для познания реального мира в целом. В нашем курсе мы будем рассматривать в основном бинарные отношения, но чтобы увидеть общность методических подходов к изучению в начальном курсе математики конкретных отношений, понять важнейшие математические идеи, связанные с отношениями, учителю надо знать, какова математическая сущность любого отношения, какими свойствами они могут обладать, какие основные виды отношений изучает математика.
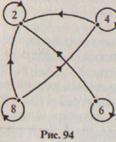
Чтобы определить общее понятие бинарного отношения на множестве, поступим так же, как и в случае с соответствиями, т.е. рассмотрим сначала конкретный пример. Пусть на множестве X = <2, 4, 6, 8>задано отношение «меньше». Это означает, что для любых двух чисел из множества X можно сказать, какое из них меньше: 2
Вообще бинарные отношения на множестве X определяют следующим способом:
Определение. Бинарным отношением на множестве X называется всякое подмножество декартова произведения Х х Х.
Так как в дальнейшем мы будем рассматривать только бинарные отношения, то слово «бинарные», как правило, будем опускать.
Условимся отношения обозначать буквами R, S, T, P и др.
Утверждение о том, что элементы х и у находятся в отношении R, можно записывать так: (х, у) € R или хRу. Последняя запись читается: «Элемент х находится в отношении R с элементом у».
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Лекция 2. Отношения на множестве, их свойства.



Если множества X и Y совпадают, X = Y, то говорят не о соответствии, а об отношении между элементами множества X.
Бинарные соответствия между X и X называют бинарными отношениями на множестве X.
Например, если X – множество людей, то соответствия «Человек х – друг человека у», «х живет в одном доме с у», «Человек х – отец человека у» являются отношениями между людьми.
Отношение на множестве X задано, если указано множество Г, являющееся подмножеством декартова произведения Х×Х.
Отношения, как и соответствия, принято обозначать буквами R, S, T, Q и др. и писать xRy, xSy и т. д.
Множество X называют областью задания отношения R, а множество Г – графиком отношения R.
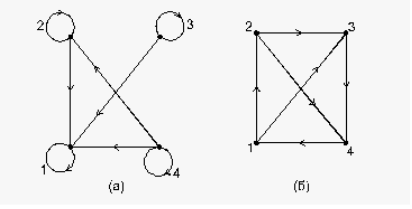
Рассмотрим, например, на множестве Х= <1; 2; 3; 4>отношение «х>у». График этого отношения – множество Г=<(2; 1); (3; 1); (3; 2); (4; 1); (4; 2); (4; 3)>, состоящее из всех тех пар (х; у), х€Х, у€Х, для которых х>у.
Способы задания отношения:
1. Перечисление упорядочных пар или графиком Г,
2. Словесным описанием,
3. Ориентированным графом,
4. Графиком в ПДСК (только для числовых множеств),
5. Таблицей (например, график дежурства – задает соответствие между учениками и днями недели),
6. Аналитически или формулой (например, у=х+5).
Чтобы наглядно представить отношение R в множестве X, изобразим точками элементы этого множества, а затем проведем стрелки от х к у для всех пар точек (х; у) таких, что xRy. Полученный чертеж называют графом отношения R, а точки, изображающие элементы множества X, вершинами графа
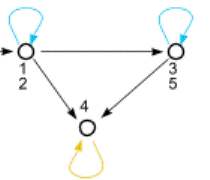
Построим, например, граф отношения R: «х≤у», заданного на множестве
Х= < 1/2; 3/5;4>. Для этого рисуем диаграмму множества X, изобразив элементы этого множества точками. Затем проводим стрелки от х к у для всех пар (x; у) таких, что х меньше или равент у. Получаем граф отношения «х≤у», заданного на множестве Х= <1>.
Каждое из этих чисел равно самому себе, поэтому для каждой точки х, изображающей элемент множества X, рисуем стрелку, начало и конец которой совпадают с х. Стрелку на графе, у которой начало и конец совпадают, называют петлей. Следовательно, граф отношения R в каждой вершине имеет петли.
Пусть на множестве X задано некоторое отношение R
1. Отношение R называется рефлексивным, если для любого х из множества X истинно xRx. Другими словами, отношение R на множестве X рефлексивно, если каждый элемент х £ X находится в отношении R с самим собой.
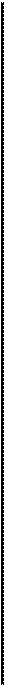
2. Отношение R называется антирефлексивным, если ни один элемент х из множества X не находится в отношении R с самим собой.
Например, отношение «Прямая х перпендикулярна прямой у» на множестве прямых плоскости антирефлексивно, так как ни одна прямая не перпендикулярна самой себе.
Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «Точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны самим себе, а точки, не лежащие на прямой l, себе не симметричны.
3. Отношение R называется симметричным, если для любых элементов х и у из множества X из xRy следует yRx.
Так, симметрично отношение параллельности на множестве прямых плоскости: если прямая х параллельна прямой у, то и прямая у параллельна прямой х.
4. Отношение R называется асимметричным если ни для каких элементов х и у из множества X не может случиться, что одновременно и xRy, и yRx.
Примером асимметричного отношения является отношение
Свойства рефлексивности, симметричности и транзитивности наглядно иллюстрируются при изображении отношений графами. Если отношение R в множестве X рефлексивно, то граф этого отношения в каждой вершине имеет петлю.
Если отношение R симметрично, то граф вместе с каждой стрелкой, идущей из точки х в точку у, должен содержать стрелку, соединяющую те же точки, но идущую в обратном направлении.
Граф транзитивного отношения вместе со стрелками, идущими от х к у и от у к z, должен содержать и стрелку, идущую от х к z.
Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы (классификацией).
Множество X всех студентов пединститута можно разбить на подмножества, состоящие из студентов, обучающихся на одном и том же курсе. Если обучение длится четыре года, то получаем четыре подмножества: студентов первого курса, студентов второго курса, студентов третьего курса и студентов четвертого курса. Никакие два из этих множеств не имеют общих элементов (студент не может сразу учиться и на втором, и на третьем курсе), а объединением этих множеств является множество X всех студентов. Говорят, что X разбито на четыре попарно непересекающихся подмножества Х1 Х2, Х3, Х4. То же множество X можно разбить на непересекающиеся подмножества и другими способами, например, на юношей и девушек, по возрасту, на комсомольцев и не комсомольцев и т. д.
Вообще, можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:
1. Все подмножества, образующие разбиение, непусты.
2. Любые два таких подмножества не пересекаются.
3. Объединение всех подмножеств есть данное множество.
Так, множество натуральных чисел можно разбить на три подмножества – множество простых чисел, множество составных чисел и множество, состоящее из единицы. Это же множество можно разбить и на два класса – класс четных и класс нечетных натуральных чисел.
Разбиение множества на попарно-непересекающиеся подмножества лежит в основе всевозможных классификаций. Понятие «класс» и его синонимы «тип», «семейство», «род», «вид», «сорт» широко применяются во всех областях человеческой деятельности. Так, в биологии все живые организмы распределяют на типы, в сельском хозяйстве сортируют по размеру или весу фрукты, слова в словарях разбивают на подмножества, располагая их в алфавитном порядке, и т. д.
Разбиение множества на попарно-непересекающиеся подмножества часто производят по некоторому свойству, которое может принимать различные значения. Например, можно производить разбиение на классы по цвету, объединяя в один класс предметы одного и того же цвета. При этом красные предметы попадут в один класс зеленые – в другой, черные – в третий и т. д. Можно сказать, что разбиение производится на основе отношения «х имеет тот же цвет, что и у». Точно так же разбиение студентов по курсам производится на основе отношения «х учится на том же курсе, что и у».
Но не всякое отношение R между элементами множества дает возможность разбить это множество на классы. Нельзя, например, разбить на попарно-непересекающиеся подмножества множество студентов некоторого института при помощи отношения «Студент х знаком со студентом у». Действительно, если х знаком с у, то х и у окажутся в одном подмножестве. Если у знаком с г, то z должен находиться в одном подмножестве с у и, следовательно, с х. Но может случиться, что х не знаком с z. Тогда окажется, что в одном подмножестве есть люди, которые друг с другом не знакомы, а этого не должно быть при разбиении множества по указанному отношению.
С другой стороны, такие отношения, как «быть однокурсником» в множестве студентов некоторого института, «родиться в одном и том же году» в множестве людей, «иметь один и тот же остаток при делении на данное число» в множестве натуральных чисел, дают возможность разбить множество, в котором они рассматриваются, на классы. Далее мы рассмотрим, какими должны быть свойства отношения, чтобы с его помощью можно было разбить множество на классы.
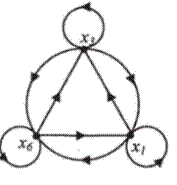
Если отношение R в множестве X обладает свойствами рефлексивности, симметричности и транзитивности, то его называют отношением эквивалентности.
Выше представлен граф отношения эквивалентности.
Примерами отношений эквивалентности являются отношения, рассмотренные нами раньше: «быть однокурсником» (на множестве студентов некоторого института), «иметь один и тот же корень» (на множестве слов) и др.
С каждым таким отношением связано разбиение множества на непересекающиеся подмножества. И это не случайно. Имеет место следующая теорема Для того чтобы отношение R позволяло разбить множество X на классы, необходимо и достаточно, чтобы R было отношением эквивалентности.
Рассмотрим несколько примеров отношений эквивалентности.
1. Отношение «Выражения х и у имеют одинаковые числовые значения» на множестве числовых выражений является отношением эквивалентности, поскольку оно
а) рефлексивно: значение выражения х совпадает со значением выражения х;
б) симметрично: если значение выражения х совпадает со значением выражения у, то и значение выражения у совпадает со значением выражения х;
в) транзитивно: если значение выражения х совпадает со значением выражения у, а значение выражения у совпадает со значением выражения z, то значение выражения х совпадает со значением выражения z.
Множество всех числовых выражений разбивается этим отношением на классы, в каждом из которых находятся выражения, значения которых попарно совпадают. Так, выражения 5+3, 23, 2+2+2+2 находятся в одном классе (их значения равны восьми), а выражения 7–3,22, 16 : 4 – в другом (их значения равны четырем).
2. Во множестве прямых на плоскости отношение параллельности является отношением эквивалентности. Прямые х и у, лежащие в одной плоскости, параллельны, если они либо не пересекаются, либо совпадают. Поэтому отношение параллельности
а) рефлексивно: х\\х для любой прямой х;
б) симметрично: если х\\у, то у\\х;
в) транзитивно: если х\\у и y\\z, то x\\z.
Отношением параллельности множество всех прямых плоскости разбивается на классы, состоящие из параллельных друг другу прямых. Такие классы называют пучками параллельных прямых.
В начальном курсе математики также встречаются отношения эквивалентности, например отношение «Выражения х и у имеют одинаковые числовые значения» в множестве числовых выражений. Выражения, принадлежащие одному и тому же классу эквивалентности, называют равными.
Отношением порядка называют антисимметричное и транзитивное отношение.
Если отношению порядка присуще еще свойство рефлексивности, то порядок нестрогий.
Если ему присуще свойство антирефлексивности, то порядок строгий.
Свойством транзитивности и асимметричности и антирефлексивности обладают многие отношения, например, отношение «больше» на множестве натуральных чисел или отношение «выше» на множестве людей, сравниваемых по росту. Это отношения строгого порядка. Об отношениях «следует за», «больше», «выше» также говорят, что они являются отношениями строгого порядка.
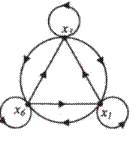
Выясним особенности графа отношения строгого порядка. Отметим, что граф отношения строгого порядка не имеет петель, нет обратных стрелок. Если из х идет стрелка в у, а из у – в z, то из х идет стрелка в z.
Наряду с отношением «х y») в математике рассматривают отношения «х≤y» («х≥у»), представляющие собой объединение отношений «х y» и «х=y»).
Говорят, что «х≤у» является отношением нестрогого порядка.
К нестрогому порядку также принадлежат, например, такие отношения: «не выше» (на множестве людей, сравниваемых по росту); «не больше» (на множестве действительных чисел); «быть делителем» (на множестве натуральных чисел).
Если на множестве рассмотреть отношение нестрогого порядка , то граф этого отношения в каждой вершине будет иметь петли ( в остальном он похож на предыдущий граф).
Множество X, на котором задано отношение порядка R (строгого или нестрогого), называется частично упорядоченным множеством. Часто говорят также, что в этом случае множество X упорядочено отношением R.
Примером такого множества является множество натуральных чисел по отношению меньше или больше.
Отношение (теория множеств)
Понятие отношения как подмножества декартова произведения формализовано в теории множеств и получило широкое распространение в языке математики во всех её ветвях. Теоретико-множественный взгляд на отношение характеризует его с точки зрения объёма — какими комбинациями элементов оно наполнено; содержательный подход рассматривается в математической логике, где отношение — пропозициональная функция, то есть выражение с неопределёнными переменными, подстановка конкретных значений для которых делает его истинным или ложным. Важную роль отношения играют в универсальной алгебре, где базовый объект изучения раздела — множество с произвольным набором операций и отношений. Одно из самых ярких применений техники математических отношений в приложениях — реляционные системы управления базами данных, методологически основанные на формальной алгебре отношений.
Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам, таким как симметричность, транзитивность, рефлексивность.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.
Во многих областях математики полезную конструкцию часто можно рассматривать как «наиболее эффективное решение» определенной проблемы. Определение универсального свойства использует язык теории категорий, чтобы сделать это определение точным и изучать его теоретическими методами.
В теории категорий есте́ственное преобразова́ние предоставляет способ перевести один функтор в другой, сохраняя внутреннюю структуру (например, композиции морфизмов). Поэтому естественное преобразование можно понимать как «морфизм функторов». Эта интуиция может быть строго формализована в определении категории функторов. Естественные преобразования — наиболее базовое определение в теории категорий наряду с функторами, поэтому оно появляется в большинстве её приложений.
В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.
Отношения. Часть I
Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические и информационные объекты, процессы их функционирования. К числу последних я отношу, например, базы данных (реляционные базы данных (РеБД)). Не менее важной считаю область принятия решений, которая состоит из двух основных статистической и алгебраической, основанной целиком на теории отношений. Образовательный уровень специалистов в этой теории близок к нулю.
Откройте учебник по специализации и там увидите в лучшем случае об эквивалентностях, которые авторами трактуются весьма своеобразно. Одного защитившегося уже ДТН спрашиваю: Вы рассматриваете отношение эквивалентности на указывая ни носителя отношения, ни конкретного отношения, как оно у Вас выглядит в записи? Ответ: как выглядит — обыкновенно. Выясняется, что он обо всем этом имеет весьма смутное представление.
Публикаций по проектированию РеБД, кроме иностранных статей назвать затрудняюсь. В 90-х годах был оппонентом, писал отзыв на диссертацию, где рассматривались и иерархические, и сетевые, и реляционные БД. Но как-то год, полтора назад опять на отзыв пришла работа, автор пишет уже только о РеБД, о нормализации отношений БД, но теоретической новизны не показал. Во многих ВУЗах читается курс о базах данных, но не о том, как их создать, создать СУБД, а как правило, о том как эксплуатировать готовую (зарубежную) БД.
Преп. состав не готов научить специалистов IТ-шников создавать отечественные СУБД, ОS, языки программирования, я уж не говорю о БИС, СБИС, заказных БИС. Здесь, по-видимому, поезд ушел давно и надолго. Так что напрасно надуваются у некоторых щеки от гордости (читай снобизма) это видно по комментариям к чужим публикациям, покажите сами, что можете, а не балуйтесь никчемными переводами и перепевками чужого ради предмета гордости — «рейтинга» и «кармы». Сказывается не только отсутствие креатива, но простой образованности и воспитания.
Вторая предметная область неразрывно, связанная с отношениями, — принятие решений. Каждый из нас постоянно занят этим. Мы без решения осознанного или неосознанного пальцем не пошевелим. Мало кто понимает, а еще меньше пишет о решениях. В основе решения любого ЛПР (лица, принимающего решение) лежит предпочтение альтернатив. А моделью предпочтения как раз и является такой тип отношений, который назван «пространством отношений предпочтения». Но кто их изучает. Когда я пришел к «специалисту» по отношениям с вопросом о количестве отношений каждого типа, он не зная ответа, «убил» встречным вопросом, а зачем это Вам?
Понятие отношения
Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров, по-видимому, не приводили.
В моей памяти есть несколько на всю жизнь запомнившихся примеров. Об отображениях и об отношениях. Расскажу вначале об отображениях. Имеется два ведерка с краской. В одном белая в другом — черная. И есть коробка с кубиками (очень много). Грани имеют рельефные номера. Сколькими способами можно раскрасить грани кубиков в два цвета? Ответ неожиданный — столькими, сколько 6-разрядных двоичных чисел, или 2 6 = 64. Поясню подробнее ф: 2→6 отображаются 2 объекта в 6. Каждая строчка таблицы- дискретное отображение фi.
Построим таблицу с 6 колонками и краскам сопоставим число белая — нуль, черная — единица, а граням кубика колонки. Начинаем с того, что все 6 граней белые — это 6-мерный нулевой вектор. Вторая строчка одна грань черная, т. е. младший разряд заполнен 1. и так до исчерпания 6-разрядных двоичных чисел. Кубики ставим в общий длинный ряд. У каждого из них как бы появился номер от 0 до 63.
Теперь отображение наоборот. Пачка листов бумаги (много) и 6 красок (фломастеры).
Фломастерами разного цвета надо пометить обе стороны бумажных листов. Сколько листов потребуется. Ответ f: 6 → 2 или 6 2 =36. Речь идет о произвольных отображениях.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Вначале простенький пример.
Подмножества будут содержать из А×А разное количество элементов (пар): одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество (Ø). Сколько же получилось подмножеств? Много, а именно 2 9 = 512 элементов.
Определение. Любое подмножество декартова произведения (у нас квадрата) множества называется отношением. Заметим, в произведении используется одно и то же множество. Если множества разные, возникает не отношение, а соответствие.
Символ отношения ставится слева от элементов R(x, y) или между ними x R y; х, у є А.
Определение Множество всех подмножеств множества А называется булеаном. Наш булеан состоит из 2 |А×А| элементов, здесь|А×А| — мощность множества.
Отношения можно задавать в разном представлении над А=
Рисунок 1.2. а)Матрица 4×4 бинарного отношения б) нумерация клеток Матрицы
Здесь используются номера клеток, заполненные единицами на рис. 1б)
— Векторное представление. Двоичный вектор для представления бинарного отношения формируется из элементов <0,1>следующим образом:
Рассмотренный пример задания отношения в векторной форме будет иметь следующий вид:
— Представление графом. Поставим в соответствие элементам множества
А =
Проведем в графе дугу от (xi) к (xj) тогда и только тогда, когда пара (xi,xj) є R (при i = j дуга (xi,xi) превращается в петлю при вершине (xi). Пример (рис. 1а) представления бинарного отношения A[4×4] графом изображен на рис.2.2.
Рисунок 2.2. Представление отношения ориентированным графом
Каталог бинарных отношений (n = 3)
Большое видится на расстоянии. Чтобы почувствовать отношения их разнообразие, мощность мне пришлось вручную создать каталог бинарных отношений над множеством из 3-х элементов, который включил все (боле 500 отношений) отношения. После этого «дошло» или «зашло»об отношениях.
Очевидно, что в каталог войдут 2 3×3 = 2 9 отношений, и каждое из них снабдим набором присущих им свойств. Ниже (табл. 3) приводится полный список всех 512 отношений над множеством А, |A| = 3, из трех элементов. Приводятся также результаты подсчета количества отношений (табл. 2), представленных сочетаниями номеров клеток декартова квадрата 3×3, различных подклассов для различных значений мощности множества-носителя (n = 3). Для каждого отношения указаны его основные свойства и принадлежность типу (табл. 3). Сокращения, используемые в каталоге раскрываются таблицей 2
Таблица 2. Количественные характеристики каталога при разных n
Сущность производимых операций с отношениями и их технику удобно пояснять на примерах, которые особенно просты и понятны для бинарных отношений. В операциях могут участвовать, два и/или более отношений. Операции, выполняемые над отдельными отношениями – унарные операции. Например, операции обращения (получение обратного) отношения, взятие дополнения, сужение (ограничение) отношения. Как пользоваться каталогом поясним примером примером.
Пример 2. Рассмотрим строку Nпр =14 таблицы каталога. Она имеет вид
Первые 9 символов строки (справа от равенства) — это двоичный вектор, соответствующий сочетанию из 9 по 2, а именно, номер первой клетки (отсчет слева направо) номер 5-й клетки матрицы бинарного отношения, т.е. элементы а1а1= а2а2 =1. Это сочетание имеет порядковый номер Ncч = 4 и сквозной номер Nпр = 14 в списке всех отношений. В остальных позициях этой строки стоят либо нули, либо единицы. Нули свидетельствуют об отсутствии свойства, соответствующего названию колонки нуля, а единицы – наличие такого свойства у рассматриваемого отношения.
Свойства и количественные характеристики отношений
Рассмотрим наиболее важные свойства отношений, которые позволят в дальнейшем выделить типы (классы) отношений, применяющиеся в реляционных базах данных в теории выбора и принятия решений и других приложениях. Далее будем обозначать отношение символом [R,Ω]. R- имя отношения, Ω — множество-носитель отношения.
1. Рефлексивность. Отношение [R,Ω] называется рефлексивным, если каждый элемент множества находится в отношении R сам с собой (рис. 2.3). Граф рефлексивного БО имеет во всех вершинах петли (дуги), а матрица отношения содержит (Е) единичную главную диагональ.
Рисунок 2.3. Рефлексивное отношение
2. Антирефлексивность. Отношение [R,Ω] называется антирефлексивным, если ни один элемент из множества не находится в отношении R сам с собой (рис. 2.4). Антирефлексивные отношения называют строгими.
Рисунок 2.4. Антирефлексивное отношение
3. Частичная рефлексивность. Отношение [R,Ω] называется частично
рефлексивным, если один или более элементов из множества не находится в отношении R сам с собой (рис. 2.5).
4. Симметричность. Отношение [R,Ω] называется симметричным, если вместе с упорядоченной парой (х, у) отношение содержит и упорядоченную пару (у, х) (рис. 2.6).
7. Транзитивность. Отношение [R,Ω] называется транзитивным, если для всяких упорядоченных пар (х, у),(у, z) є R, в отношении R найдется упорядоченная пара (х, z) є R или если R×R⊆R (рис. 2.9).
8. Цикличность. Отношение [R,Ω] называется циклическим, если для его элементов
9. Ацикличность. Отношения, в которых отсутствуют контуры называются, ациклическими. Для ациклических отношений выполняется соотношение R k ∩R = Ø для любого k > 1 (рис. 2.11).
10. Полнота (связность). Отношение [R,Ω] называется полным (связным), если для любых двух элементов (у, z) є Ω один из них находится в отношении с другим (рис 2.12). Линейность. Линейные отношения – это минимально полные отношения.
Рисунок 2.12. Линейное отношение
Итак, нами установлено, что отношения, как математические объекты, обладают определенными свойствами, определение которых приведены ранее. В следующем пункте рассмотрим существо и проявление некоторых свойств:
Количественные соотношения таких дискретных пространств представляют большой как
теоретический, так и практический интерес. Ниже рассматриваются некоторые аспекты количественных характеристик, связанных со свойствами отношений разных типов.
Операции над отношениями
Как и большинстве систем счисления с отношениями выполняются операции:
Выше было введено понятие бинарного отношения, как подмножества упорядоченных пар декартова произведения множеств, а также были рассмотрены свойства отношений. Кроме того, были упомянуты бинарные отношения и матричное представление отношений. Рассмотрим теперь понятие отношения более подробно, кроме того, рассмотрим основные операции бинарных отношений, наиболее важные из всего их множества для отношений.
Для них должны выполняться следующие условия:
Унарные операции над отношениями
9. Двойственное отношение (P d ) к отношению Р – отношение, образованное всеми теми парами, которые принадлежат универсальному отношению и не принадлежат обратному отношению (дополнение к обратному):
Двойственное и обратное отношения в совокупности содержат все пары декартова произведения A×A и не имеют общих пар, они также как и отношения Р и P образуют разбиение A×A
Сужение (РА1). Отношение [R1, A1] называется сужением отношения [R, A] на множество Ω1, если Ω1⊆ Ω и R1=R∩Ω1×Ω1. Отношение РА1 на множестве А1 ⊆ А – отношение РА1 на множестве А1, образованное всеми теми парами, которые принадлежат отношению Р и одновременно входят в состав декартова произведения А1 × А1. Другими словами, РА1 – пересечение отношений Р и А1×А1. Пусть А1 =
Операции, требующие не менее двух отношений – n-арные (n-местные). В таких операциях могут участвовать отношения только одинаковой арности. Примеры таких операций: пересечение, объединение, разность, симметрическая разность отношений и некоторые другие. Если в операции используется более чем два отношения, то она выполняется последовательно для двух первых, а затем для итогового отношения и третьего и т.д.
Иначе говоря, эти операции определены для двух отношений. При операциях над отношениями предполагается, что области задания отношений (операндов и результата) совпадают, арности отношений совпадают, и результатом операции снова является отношение той же арности. В качестве примеров будем рассматривать операции над бинарными отношениями P и Q, заданными на дискретном множестве
А =
1. Пересечение (P ∩ Q) – отношение, образованное всеми теми парами элементов из А, которые входят в оба отношения, т.е. общие для P и Q,
P ∩ Q = <(ai aj) | ((ai aj) є P) & ((ai aj) є Q)>.
Матрица отношения P ∩ Q получается как булево пересечение матриц P и Q:
При отсутствии таких общих пар говорят, что пересечение отношений пусто, т.е. оно является нуль-отношением. Пересечением отношений R1 и R2 (R1∩R2 ) называется отношение, определяемое пересечением соответствующих подмножеств из А×А.
2. Объединение (PUQ). Объединением отношений R1 и R2 (R1UR2 ) называется отношение, определяемое объединением соответствующих подмножеств из А×А. Отношение, образованное всеми парами, составляющими или отношение P, или отношение Q, т.е. парами, принадлежащими хотя бы одному из отношений (связка ∨ — или объединительная)
P U Q = <(ai aj) | ((ai aj) є P) ∨ ( (ai aj) є Q)>.
Если в множестве А×А нет других пар, не вошедших в отношение PUQ, а пересечение их нулевое, то говорят, что отношения P и Q при объединении образуют полное отношение А×А, а их система – разбиение этого полного отношения. Объединение матриц отношений образуется как булева сумма матриц отношений:
3.Разность (P\Q) – отношение, образованное теми парами из Р, которые не входят в отношение Q
P\Q = <(ai aj) | ((ai aj) є P)&((ai aj)∉Q)>.
Разность для отношений в матричном представлении имеет вид
4. Умножение отношений. Упорядоченные пары, образующие отношения могут содержать одинаковые элементы, а могут и не содержать. Среди пар, имеющих в своем составе одинаковые элементы, выделим такие упорядоченные пары, которые назовем смежными (примыкающими) и которые имеют во второй паре 1-й элемент, а в первой паре 2-й элемент один и тот же. Определим произведение смежных пар как упорядоченную пару:
( ai ak)∙( ak aj) => (ai aj).
В терминах теории графов сказанное означает, что смежные пары образуют маршрут из точки (ai) в точку (aj) транзитом через точку (ak), состоящий из 2-х смежных дуг. Произведение этих дуг – третья дуга из точки (ai) в точку (aj), реализующая переход между крайними точками маршрута в том же направлении, минуя промежуточную точку (ak). Говорят, что дуга (ai aj) замыкает эти точки напрямую.
5. Симметрическая разность (P∆Q) – отношение, образованное теми парами, которые входят в объединение PUQ, но не входят в пересечение P∩Q. Другая форма определения объясняет название операции: P∆Q образовано теми упорядоченными парами, которые являются объединением разностей P\Q и Q\P. Таким образом, выражение для симметрической разности записывается двумя разными способами:
P∆ Q = (PU Q)\(P ∩ Q) = (P\Q)U (Q\P).
Матрица симметрической разности имеет вид:
Из последней записи следует, что операция симметрической разности допускает перестановку операндов, т. е. коммутативна.
5. Композиция или произведение (P∙Q) – отношение, образованное всеми парами, для которых выполняется:
P∙Q = <(ai aj)|((ai ak) є P) & ((ak aj) є Q)>.
Другими словами, каждая упорядоченная пара в результирующем отношении есть результат умножения смежных пар, из которых 1-я пара принадлежит первому сомножителю-отношению, 2-я – второму сомножителю-отношению. Операция композиции не коммутативна.
Композиция (Р◦Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда существует Z є M такое, что (x, z) є P и (z, y) є Q.
При матричном представлении отношений матрица композиции отношений равна булеву произведению матриц исходных отношений:
Частный случай композиции отношений – квадрат отношения.
Можно показать, используя индукцию, что n-я степень отношения определяется рекуррентно по формуле:P n =P n-1 ◦Р, это означает, что пара (x,y) є P n в том случае, когда в матрице Р существует цепочка элементов: такая, что (xi, xi+1)є P, 1 Литература