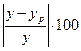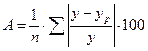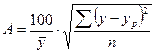Что такое ошибка аппроксимации
Ошибки аппроксимации
Практически всегда фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, тем лучше подобрано уравнение регрессии. Величина отклонений фактических и расчетных значений результативного признака 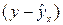
Отклонения 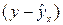
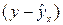
Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.
Поскольку 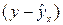
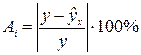
Эти ошибки уже поддаются сравнению, но они оценивают каждое наблюдение в отдельности. Такую ошибку принято называть относительной ошибкой аппроксимации.
Чтобы оценить качество модели в целом, можно определить среднюю ошибку аппроксимации, представляющую собой среднюю арифметическую относительных ошибок аппроксимации по всем наблюдениям, включаемым в модель:
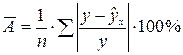
Модель считается подобранной достаточно хорошо, если средняя ошибка аппроксимации не превышает 8–10%. Предпочтение отдается модели с наименьшей ошибкой 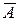
Возможно и другое определение средней ошибки аппроксимации:
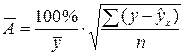
Значения ошибок, рассчитанных по разным формулам будут отличаться друг от друга. Наиболее часто используется первый вариант расчета средней ошибки аппроксимации.
Средняя ошибка аппроксимации



Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака каждому наблюдению представляет собой ошибку аппроксимации. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.
Поскольку 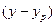
Такие ошибки являются относительными, а отклонения 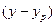
Для того, чтобы иметь общее суждение о качестве модели из относительных отклонений, находят среднюю ошибку аппроксимации как
Ошибка аппроксимации в пределах 5-7 % свидетельствует о хорошем подборе модели к исходным данным.
Возможно и другое определение средней ошибки аппроксимации:
Для расчета средней ошибки аппроксимации в стандартных программах чаще используется вторая формула.
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
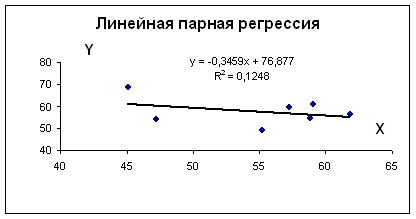
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Для наших данных система уравнений имеет вид
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Что такое ошибка аппроксимации
Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии. [c.29]
Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора. [c.29]
Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]
Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]
Чем продолжительнее период, по данным которого построены модели, тем меньше темп роста ошибки аппроксимации при прочих равных условиях. Следовательно, чем короче период упреждения, тем короче следует брать и период анализа, и, наоборот, при долгосрочном планировании необходимо использовать максимально возможную продолжитель- [c.64]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]
Средняя ошибка аппроксимации [c.94]
Средняя ошибка аппроксимации. [c.95]
В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4). [c.144]
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D). [c.151]
Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]
После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]
Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%. [c.123]
Подобное обоснование является приблизительным и нуждается в дальнейшем уточнении с помощью ошибки аппроксимации. [c.50]
Наибольшее значение ошибки аппроксимации свидетельствует о том, что оцениваемая модель дает наиболее адекватное описание формы взаимосвязи. Причем ошибка аппроксимации не должна превышать 0,2, или 20%. [c.52]
Подставляя последовательно значения времени /, получим теоретические уровни товарооборота. Ошибка аппроксимации для прямолинейной формы тренда составит [c.184]
Далее рассчитывается ошибка аппроксимации для функции тренда в виде параболы второго порядка по формуле [c.187]
Для повышения надежности прогноза потребности в нефтепродуктах по управлению в целом и определения границ его достоверности на всех этапах прогнозирования предусматривается проведение верификации. При верификации принимаются в расчет не все частные прогнозы, а только те из них, которые удовлетворяют требованиям статистической надежности, дают наименьшую ошибку аппроксимации, подтверждаются проверкой ретроспективным методом и дают результаты, близкие к фактическим значениям за последний год ретроспективного периода. Для облегчения проведения расчетов по алгоритму (рис. 7) на каждом этапе прогнозирования (кратко-, средне- и долгосрочный прогнозы) составляются подсобные таблицы по форме 010107 (табл. 6). [c.63]
Очевидно, что ошибки аппроксимации носят непериодический характер. В противном случае нужно было бы повторить всю процедуру, используя в качестве исходной выборки эти ошибки, и повторять ее до тех пор, пока не будут выделены все значимые гармоники. [c.137]
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. [c.6]
А = 8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость. [c.15]
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. [c.16]
Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера. [c.32]
Оцените качество модели. Для этого а) определите ошибку аппроксимации t б) найдите показатель тесноты связи прибыли с исследуемым в мо- [c.33]
Оцените с помощью средней ошибки аппроксимации качество уравнений. [c.38]
Оцените качество уравнений с помощью средней ошибки аппроксимации. [c.42]
Оцените качество уравнения через среднюю ошибку аппроксимации. [c.92]
Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений. [c.166]
СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ [c.87]
Параметры моделей и выбор формы связи, определяющие уровень затрат в зависимости от значений отобранных факторов, вычисляются по методике, изложенной в работе [51]. Затем исследуется характер изменения случайных отклонений (ошибки аппроксимации) по каждому НГДУ отдельно. Если обнаружится определенная закономерность их изменений, то вычисляется функция их изменения во времени, и далее плановый [c.68]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Дальнейший анализ выглядит чаще как моделирование взаимосвязей и оценка тесноты взаимозависимости (корреляционно-регрессионный анализ). Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Это относительная ошибка аппроксимации, средняя квадратическая ошибка аппроксимации (6ОСТ) (чем они меньше, тем лучше уравнение) и коэффициент множественной детерминации (R2) или коэффициент множественной корреляции (R) (чем ближе он к 1, тем более вероятность, что уравнение регрессии носит совершенно случайный характер). Для проверки значимости используют F-критерий с распределением Фишера. [c.670]
Смотреть страницы где упоминается термин Ошибка аппроксимации
Определение средней ошибки аппроксимации
На практике часто приходится сталкиваться с задачей сглаживания экспериментальных данных – задача аппроксимации.
Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции наиболее близко проходящей около данных точек или около данной непрерывной функции.
Аппроксимация – процесс подбора эмпирической функции f (х) для установления из опыта функциональной зависимости y= f (х). Эмпирические формулы служат для аналитического представления опытных данных.
Средняя ошибка аппроксимации среднее отклонение расчетных значений от фактических. Допустимый предел значений средней ошибки аппроксимации не более 8-10% Средний коэффициент эластичности показывает, на сколько процентов изменится результат (результативный признак) от своей средней величины при изменении фактора x (признак-фактор) на 1% от своего среднего значения. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации:

Фактическое значение результативного признака y отличается от теоретических значений, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, и лучше качество модели.
Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации.
Поскольку может быть, как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Если А до 10-12%, то можно говорить о хорошем качестве модели.
Варианты заданий
Библиографический список