что такое хаотичное движение

Теория хаоса

Что такое «странные аттракторы» и как они помогают синоптикам

Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.

В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.

Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.

Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.

В своем выступлении Лоренц выделил несколько ключевых идей:

⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.

⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.

Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.

В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.

Система Лоренца

Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):

⦁ Уравнение движения в векторном виде:

⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:

⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:

В оригинале эти три составляющие дают следующую систему:

Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:

Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:

С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.

Хаотическое движение

Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.

Изобразим движение двух точек, расстояние между которыми изначально невелико:

Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.

Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:

Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…

Странный аттрактор Лоренца

Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract — «притягивать»).

Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)

Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.

Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.

Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.

Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».

Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.

Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:

Немного математики

Система Лоренца обладает несколькими замечательными свойствами:

⦁ Правая часть системы не имеет свободных членов, то есть она однородна.

Источник

«ХАОТИЧЕСКОЕ» ДВИЖЕНИЕ

Если бы народы знали, из-за чего мы воюем, то никогда не удалось бы устроить хоть одну приличную войну.
(Фридрих II, Великий, король Пруссии)

Движения выполняемые в рукопашном бою на пределе физических и психических возможностей, как правило лишаются какой либо технической составляющей и приобретают так сказать «хаотический характер — на первый план выходят только их скорость и сила. (Данные движения так же можно назвать «неправильными» движениями рукопашного боя, которые лишены не только какой либо технической основы, но и зачастую и всякой осознанности.) С другой стороны именно в хаотических движениях и может быть скрыта возможность для увеличения эффективности используемой техники — приблизить движения системы рукопашного боя по скорости и силе к «хаотическим» движениям отставив при этом их техническую составляющую.
Таким образом «хаотичными», можно назвать движения которые выполняются в реальном рукопашном бою без всякой предварительной подготовки, более того они даже являются как бы «последними» движениями реального боя в таких случаях как:
1. нарушение или изменение физического состояния
1.1. ведение боя на предельных скоростях
1.2. нехватка времени для проведения защиты
1.3. необычные условия для проведения защиты
1.4. получение травм или ранений
1.5. утомление
2. нарушение или изменение психического состояния
2.1. растерянность
2.2. страх
2.3. злость
2.4. разрушение осознанной системы боя

То есть это случаи, когда человек выходит за границы не только своей подготовки но и за пределы своих физических и психических возможностей, и просто не может справиться с изменившимися условиями боя обычными способами. (например — когда боксер сталкивается с борцом, когда поскользнулся и потерял равновесие, да даже и когда просто промахнулся и из-за этого «провалился», а противник атаковал в этот момент, «сбив» таким образом позицию.) И поэтому можно сказать что стремление к некоей универсализации, к предвидению и рассмотрению всех возможных случаев атаки и защиты – конечно накапливает опыт, но с другой стороны — в реальном рукопашном бою все таки одним из определяющих факторов является эффект неожиданности неизбежность столкновения с последствиями которого и следует учитывать.
Очевидно, что для эффективного ведения реального рукопашного боя необходима как способность вести бой в таких «хаотических» движениях, так и способы быстрого выхода из этого состояния – так сказать перегруппировка и возвращение боевого контроля. И думаю, что наиболее рациональным способом преодоления этого состояния является использование дыхательных техник – именно дыхание и должно стать способом контроля практически над всеми действиями в рукопашном бою.
Всякие точные движения будут сбиты в реальном рукопашном бою и он может легко превратиться в некое соревнование древних инстинктов, где выживает тот кто действует более инстинктивно или тот кому просто «повезет», а вся техника рукопашного боя в конечном итоге свестись к использованию только лишь инстинктивных боевых движений. Поэтому и суть изучения техники реального рукопашного боя по большому счету заключается в том, чтобы осознать и отточить именно такие инстинктивные движения, так как именно они и являются тем ключевым элементом и который сможет дать необходимую скорость и силу для эффективного ведения реального боя. (то есть по большому счету всякое движение в реальном рукопашном бою должно основываться на страхе, инстинкте и злости, а соответственно основной задачей для определения и отработки ведения рукопашного боя — сделать эти инстинктивные движения максимально осознанными.)

И напоследок — удивительное видео — бой на топорах — кому это может понадобиться — шел и мужик напал на другого с топором — и а у этого другого тоже случайно оказался топор — какая удача. И начали они «драться на топорах»

Добавить комментарий Отменить ответ

ПОИСК по сайту

Рубрики

ТРАНСЛЯЦИИ ПО ВИДАМ СПОРТА:

Свежие комментарии

Рубрики

© 2014-2021 Система реального рукопашного боя

Источник

Основные положения молекулярно-кинетической теории и их опытное обоснование

Молекулярно-кинетическая теория (МКТ) – это учение, которое объясняет тепловые явления в макроскопических телах и внутренние свойства этих тел движением и взаимодействием атомов, молекул и ионов, из которых состоят тела. В основе МКТ строения вещества лежат три положения:

Эти основные положения подтверждаются экспериментально и теоретически.

Состав вещества

Хаотическое движение частиц

Непрерывное хаотическое движение частиц подтверждается броуновским движением и диффузией. Хаотичность движения означает, что у молекул не существует каких-либо предпочтительных путей и их движения имеют случайные направления. Это означает, что все направления равновероятны.

Диффузия (от латинского diffusion – растекание, распространение) – явление, когда в результате теплового движения вещества происходит самопроизвольное проникновение одного вещества в другое (если эти вещества соприкасаются).

Взаимное перемешивание веществ происходит по причине непрерывного и беспорядочного движения атомов или молекул (или других частиц) вещества. С течением времени глубина проникновения молекул одного вещества в другое увеличивается. Глубина проникновения зависит от температуры: чем выше температура, тем больше скорость движения частиц вещества и тем быстрее протекает диффузия.

Диффузия наблюдается во всех состояниях вещества – в газах, жидкостях и твёрдых телах. Примером диффузии в газах служит распространение запахов в воздухе при отсутствии прямого перемешивания. Диффузия в твёрдых телах обеспечивает соединение металлов при сварке, пайке, хромировании и т.п. В газах и жидкостях диффузия происходит намного быстрее, чем в твёрдых телах.

Взаимодействие частиц

Существование устойчивых жидких и твёрдых тел объясняется наличием сил межмолекулярного взаимодействия (сил взаимного притяжения и отталкивания). Этими же причинами объясняется малая сжимаемость жидкостей и способность твёрдых тел сопротивляться деформациям сжатия и растяжения.

Силы межмолекулярного взаимодействия имеют электромагнитную природу – это силы электрического происхождения. Причиной этого является то, что молекулы и атомы состоят из заряженных частиц с противоположными знаками зарядов – электронов и положительно заряженных атомных ядер. В целом молекулы электрически нейтральны. По электрическим свойствам молекулу можно приближённо рассматривать как электрический диполь.

Силы притяжения принято считать отрицательными, а силы отталкивания – положительными, хотя это деления является условным.

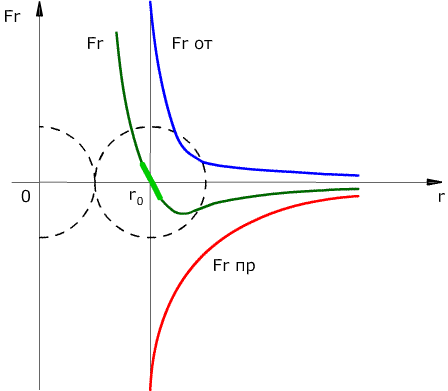
Сила взаимодействия между молекулами имеет определённую зависимость от расстояния между молекулами. Эта зависимость изображена на рис. 1.1. Здесь показаны проекции сил взаимодействия на прямую, которая проходит через центры молекул.

Рис. 1.1. Зависимость межмолекулярных сил от расстояния между взаимодействующими атомами.

Как видим, по мере уменьшения расстояния между молекулами r сила притяжения F_{r пр} увеличивается (красная линия на рисунке). Как уже было сказано, силы притяжения принято считать отрицательными, поэтому по мере уменьшения расстояния кривая уходит вниз, то есть в отрицательную зону графика.

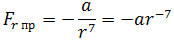(1.1)

где a – коэффициент, зависящий от вида сил притяжения и строения взаимодействующих молекул.

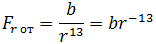(1.2)

где b – коэффициент, зависящий от вида сил отталкивания и строения взаимодействующих молекул.

На расстоянии r = r₀ (это расстояние примерно равно сумме радиусов молекул) силы притяжения уравновешивают силы отталкивания, а проекция результирующей силы F_r = 0. Этому состоянию соответствует наиболее устойчивое расположение взаимодействующих молекул.

В общем случае результирующая сила равна:

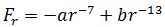(1.3)

При r > r₀ притяжение молекул превосходит отталкивание, при r
Броуновское движение (или брауновское движение ) – это непрерывное хаотическое движение малых частиц, взвешенных в жидкости или газе (при этом подразумевается, что сила тяжести не влияет на их движение).

Это явление впервые наблюдал Роберт Броун (Браун, годы жизни 1773 – 1858), когда рассматривал в микроскоп движение цветочной пыльцы, взвешенной в воде. В наше время для таких наблюдений используют маленькие части краски гуммигут, которая не растворяется в воде. В газе броуновское движение совершают, например, взвешенные в воздухе частицы пыли или дыма.

Броуновское движение частицы возникает потому, что импульсы, с которыми молекулы жидкости или газа действуют на эту частицу, не компенсируют друг друга. Молекулы среды (то есть молекулы газа или жидкости) движутся хаотично, поэтому их удары приводят броуновскую частицу в беспорядочное движение: броуновская частица быстро меняет свою скорость по направлению и по величине.

Броуновское движение – это тепловое движение, интенсивность которого возрастает с ростом температуры среды и продолжается неограниченно долго без каких-либо видимых изменений.Интенсивность броуновского движения также возрастает с уменьшением размера и массы частиц, а также при уменьшении вязкости среды.

Броуновское движение служит наиболее наглядным экспериментальным подтверждением существования атомов (молекул) и их хаотического теплового движения. Полнаямолекулярно-кинетическая теория броуновского движения была дана в 1905 – 1906 годах немецким учёным Альбертом Эйнштейном (1879 – 1955) и польским физиком Марианом Смолуховским (1872 – 1917). В 1908 – 1911 годах французский учёный Жан Перрен (1870 – 1942) провёл серию экспериментов по изучению броуновского движения и окончательно подтвердил закономерности этого движения, предсказанные на основе молекулярно-кинетической теории.

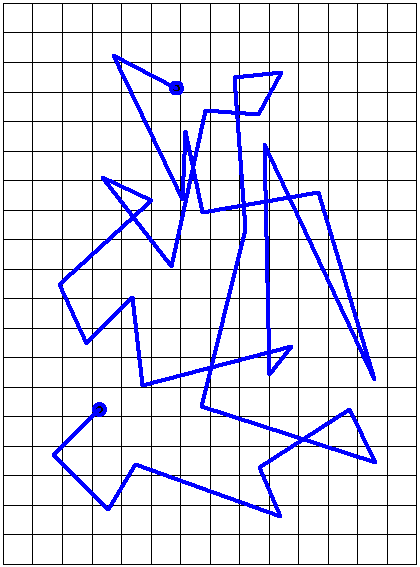
Рис. 1.2. Траектория движения броуновской частицы (частиц краски гуммигута в воде по Перрену).

Броуновское движение, например, в метрологии, является основной причиной, по которой точность чувствительных измерительных приборов ограничена, потому что тепловое движение атомов деталей приборов и окружающей среды вызывает дрожание стрелок измерительных приборов.

Масса и размер молекул

Многие опыты показывают, что размер молекулы очень мал. Линейный размер молекулы или атома можно найти различными способами. Например, с помощью электронного микроскопа, получены фотографии некоторых крупных молекул, а с помощью ионного проектора (ионного микроскопа) можно не только изучить строение кристаллов, но определить расстояние между отдельными атомами в молекуле.

Для характеристики атомов используют представление об атомных радиусах, которые дают возможность приближённо оценить межатомные расстояния в молекулах, жидкостях или твёрдых телах, так как атомы по своим размерам не имеют чётких границ. То естьатомный радиус – это сфера, в которой заключена основная часть электронной плотности атома (не менее 90…95%).

Размер молекулы настолько мал, что представить его можно только с помощью сравнений. Например, молекула воды во столько раз меньше крупного яблока, во сколько раз яблоко меньше земного шара.

Моль вещества

Массы отдельных молекул и атомов очень малы, поэтому в расчётах удобнее использовать не абсолютные значения масс, а относительные.

Относительная молекулярная масса (или относительная атомная масса) вещества М_r – это отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода.

где m₀ – масса молекулы (или атома) данного вещества, m_0C – масса атома углерода.

Относительная молекулярная масса вещества может быть вычислена путём сложения относительных атомных масс элементов, входящих в состав молекулы вещества. Относительная атомная масса химических элементов указана в периодической системе химических элементов Д.И. Менделеева.

В периодической системе Д.И. Менделеева для каждого элемента указана атомная масса, которая измеряется в атомных единицах массы (а.е.м.). Например, атомная масса магния равна 24,305 а.е.м., то есть магний в два раза тяжелее углерода, так как атомная масса углерода равна 12 а.е.м. (это следует из того, что 1 а.е.м. = 1/12 массы изотопа углерода, который составляет большую часть атома углерода).

Зачем измерять массу молекул и атомов в а.е.м., если есть граммы и килограммы? Конечно, можно использовать и эти единицы измерения, но это будет очень неудобно для записи (слишком много чисел придётся использовать для того, чтобы записать массу). Чтобы найти массу элемента в килограммах, нужно атомную массу элемента умножить на 1 а.е.м. Атомная масса находится по таблице Менделеева (записана справа от буквенного обозначения элемента). Например, вес атома магния в килограммах будет:

Массу молекулы можно вычислить путём сложения масс элементов, которые входят в состав молекулы. Например, масса молекулы воды (Н₂О) будет равна:

Количество вещества принято считать пропорциональным числу частиц. Количество вещества – это физическая величина, характеризующая относительное число молекул и атомов в теле. Единица количества вещества называется молем (моль).

Постоянная Авогадро

Количество вещества ν равно отношению числа молекул в данном теле к числу атомов в 0,012 кг углерода, то есть количеству молекул в 1 моле вещества.

где N – количество молекул в данном теле, N_A – количество молекул в 1 моле вещества, из которого состоит тело.

N_A – это постоянная Авогадро. Количество вещества измеряется в молях.

Постоянная Авогадро – это количество молекул или атомов в 1 моле вещества. Эта постоянная получила своё название в честь итальянского химика и физика Амедео Авогадро (1776 – 1856).

В 1 моле любого вещества содержится одинаковое количество частиц.

Молярная масса – это масса вещества, взятого в количестве одного моля:

где m₀ – масса молекулы.

Молярная масса связана с относительной молекулярной массой соотношением:

Масса любого количества вещества m равна произведению массы одной молекулы m₀ на количество молекул:

Количество вещества равно отношению массы вещества к его молярной массе:

Массу одной молекулы вещества можно найти, если известны молярная масса и постоянная Авогадро:

Более точное определение массы атомов и молекул достигается при использовании масс-спректрометра – прибора, в котором происходит разделение пучком заряженных частиц в пространстве в зависимости от их массы заряда при помощи электрических и магнитных полей.

Как видим, молярная масса (в граммах) практически равна атомной массе, указанной для элемента в таблице Менделеева. Поэтому когда указывают атомную массу, то обычно делают так:

Движение молекул в газах, жидкостях и твёрдых телах

Молекулярно-кинетическая теория даёт объяснение тому, что все вещества могут находиться в трёх агрегатных состояниях: в твёрдом, жидком и газообразном. Например, лёд, вода и водяной пар. Часто плазму считают четвёртым состоянием вещества.

Агрегатные состояния вещества (от латинского aggrego – присоединяю, связываю) – состояния одного и того же вещества, переходы между которыми сопровождаются изменением его физических свойств. В этом и заключается изменение агрегатных состояний вещества.

Во всех трёх состояниях молекулы одного и того же вещества ничем не отличаются друг от друга, меняется только их расположение, характер теплового движения и силы межмолекулярного взаимодействия.

Движение молекул в газах

В газах обычно расстояние между молекулами и атомами значительно больше размеров молекул, а силы притяжения очень малы. Поэтому газы не имеют собственной формы и постоянного объёма. Газы легко сжимаются, потому что силы отталкивания на больших расстояниях также малы. Газы обладают свойством неограниченно расширяться, заполняя весь предоставленный им объём. Молекулы газа движутся с очень большими скоростями, сталкиваются между собой, отскакивают друг от друга в разные стороны. Многочисленные удары молекул о стенки сосуда создаютдавление газа.

Движение молекул в жидкостях

Время оседлой жизни уменьшается с повышением температуры. Расстояние между молекулами жидкости меньше размеров молекул, частицы расположены близко друг к другу, а межмолекулярное притяжение велико. Тем не менее, расположение молекул жидкости не является строго упорядоченным по всему объёму.

Жидкости, как и твёрдые тела, сохраняют свой объём, но не имеют собственной формы. Поэтому они принимают форму сосуда, в котором находятся. Жидкость обладает таким свойством, кактекучесть. Благодаря этому свойству жидкость не сопротивляется изменению формы, мало сжимается, а её физические свойства одинаковы по всем направлениям внутри жидкости (изотропия жидкостей). Впервые характер молекулярного движения в жидкостях установил советский физик Яков Ильич Френкель (1894 – 1952).

Движение молекул в твёрдых телах

Молекулы и атомы твёрдого тела расположены в определённом порядке и образуют кристаллическую решётку. Такие твёрдые вещества называют кристаллическими. Атомы совершают колебательные движения около положения равновесия, а притяжение между ними очень велико. Поэтому твёрдые тела в обычных условиях сохраняют объём и имеют собственную форму.

Тепловое равновесие

Тепловое равновесие (или термодинамическое равновесие) – это такое состояние, при котором все макроскопические параметры сколь угодно долго остаются неизменными.

В состоянии термодинамического равновесия не происходит теплообмен с окружающими телами, не изменяются объём и давление тела, отсутствуют взаимные превращения жидкостей, газов и твёрдых тел.

Температура и её физический смысл

Любая термодинамическая система при неизменных внешних условиях самопроизвольно переходит в состояние термодинамического равновесия.

Температура тела – это физический параметр, одинаковый во всех частях системы тел, которая находится в состоянии термодинамического равновесия.

При тепловом равновесии микроскопические процессы внутри тела (движение частиц и взаимодействие частиц) не прекращаются. Термодинамическая система может находиться в различных состояниях теплового равновесия, каждому из которых соответствует определённое значение температуры. При теплообмене между телами происходит обмен энергией: тела с большей энергией передают свою энергию телам с меньшей энергией. Направление теплообмена между ними указывает разность температур тел. То есть энергия передаётся от более горячего тела к менее горячему.

Температура и её измерение

Для измерения температуры используется тот факт, что с изменением температуры тела изменяются почти все его физические свойства: длина, объём, плотность, электрическое сопротивление, упругие свойства и др. Основой для измерения температуры может являться изменение какого-либо свойства термометрического тела.

Термометрическое тело – это тело, для которого известна зависимость какого-либо свойства данного тела от температуры. Термометрическим телом может быть, например, жидкость или газ, для которого известна зависимость изменения его объёма от температуры.

Эмпирическая шкала – это температурная шкала, установленная с помощью термометрического тела.

Наиболее распространён способ измерения температуры с помощьюжидкостного термометра, в котором используется расширение жидкости (изменение объёма) при нагревании.

При градуировке термометра отмечают опорные точки, расстояние между которыми на шкале делят на равные части, которые называются градусами.

Шкала температур Цельсия

Для практического употребления по решению IX Генеральной конференции по мерам и весам в 1948 году была принята международная стоградусная температурная шкала – шкала Цельсия.

Шведский физик и астроном Андерс Цельсий (1701 – 1744) в 1742 году предложил шкалу термометра, в которой за ноль градусов (начало отсчёта температуры) принял температуру таяния льда, а за сто градусов – температуру кипения воды при нормальном атмосферном давлении в 1,01325 * 10 5 Па. Изменение длины столба жидкости в термометре на одну сотую долю длины между отметками 0 и 100 °С соответствует изменению температуры на 1 °С. По данной шкале единица измерения температуры – градус Цельсия.

Перевести градусы из Цельсия в Фаренгейт можно так:

Перевод из Фаренгейта в Цельсий:

Здесь t_F – температура по Фаренгейту, t_C – температура по Цельсию

Источник