что такое функция в алгебре 7 класс определение
Что такое функция в математике
Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.
| Сколько времени двигается автомобиль | Сколько км проедет автомобиль |
|---|---|
| 1 час | 60 км |
| 2 часа | 120 км |
| 3 часа | 180 км |
Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.
Обозначим за « x » время автомобиля в пути.
Обозначим за « y » расстояние, пройденное автомобилем.
Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).
Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.
Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».
Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:
Функцией называют зависимость « y » от « x ».
Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.
Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
Примеры других функций:
Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).
Способы задания функции
Задание функции формулой
Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента « x » найти значение функции « y ».
Например, рассмотрим функцию, заданную формульным способом.
Запишем расчет следующим образом.
Табличный способ задания функции
С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля « y(x) = 60x ».
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений « y » для произвольно выбранных значений « x ».
Будьте внимательны, когда подставляете значение « x » в функцию,
у которой перед « x » есть минус.
Нельзя терять знак минуса, который стоит перед « x ».
При подстановки отрицательного числа в функцию вместо « x » обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.
Подставим в функцию « y(x) = −x + 4 » вместо « x » отрицательное число « −1 ».
Неправильно
Правильно
Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции « y(x) = −x + 4 ».
| x | y |
|---|---|
| −1 | 5 |
| 0 | 4 |
| 1 | 3 |
Графический способ задания функции
Теперь давайте разберемся, что называют графиком функции и как его построить.
Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.
Рассмотрим функцию « y(x) = −2x + 1 ».
Результаты запишем в таблицу.
| x | Расчет |
|---|---|
| −1 | y(−1) = −2 · (−1) + 1 = 2 + 1 = 3 |
| 0 | y(0) = −2 · 0 + 1 = 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Назовем каждую полученную точку и запишем их координаты в новую таблицу.
| Имя точки | x | y |
|---|---|---|
| (·) A | −1 | 3 |
| (·) B | 0 | 1 |
| (·) C | 1 | −1 |
Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции « y(x) = −2x + 1 ».
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо « x ».
Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо « x ».
Полученный график функции « y(x) = −2x + 1 » это бесконечное множество точек, которые лежат на одной прямой.
При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.
Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.
Понятие функции
Урок 12. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие функции»
· ввести понятия «функциональная зависимость»;
· узнать о способах задания функции;
· познакомиться с историей функции.
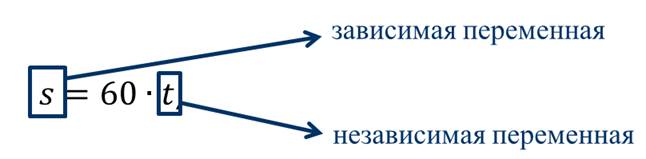
Изучение темы начнём с рассмотрения нескольких примеров.
В рассмотренном примере переменную t называют независимой переменной, так как её значения мы выбирали произвольно. А переменную s называют зависимой переменной, так как её значения определяются выбранными значениями переменной t.
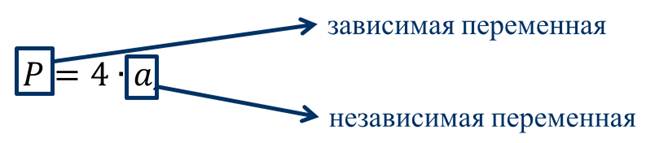
Давайте рассмотрим ещё один пример.
В этом примере переменная а является независимой переменной, а переменная Р – зависимой переменной.
В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называю функциональной зависимостью или функцией.
Независимую переменную называют также аргументом, а зависимую – функцией от этого аргумента.
Так в рассмотренных примерах путь, пройденный автомобилем, является функцией от времени движения автомобиля. А периметр квадрата является функцией от его стороны.
Значения, которые принимает независимая переменная, образуют область определения функции.
Все значения зависимой переменной называют значениями функции.
А сейчас выполним следующее упражнение.
В семнадцатом веке французские математики Рене Декарт и Пьер Ферма впервые начали выражать зависимость между переменными при помощи формулы.
В рассмотренных выше примерах функции задавались с помощью формулы. И этот способ задания функции является более распространённым. Но давайте рассмотрим ещё несколько примеров.
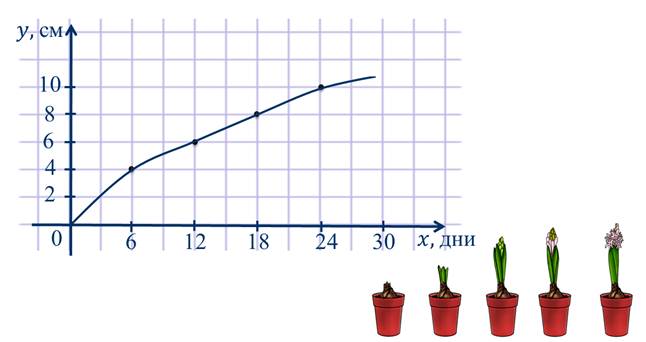
На рисунке показано, как изменялась высота гиацинта в зависимости от его возраста. Рост указан в сантиметрах, а его возраст в днях.
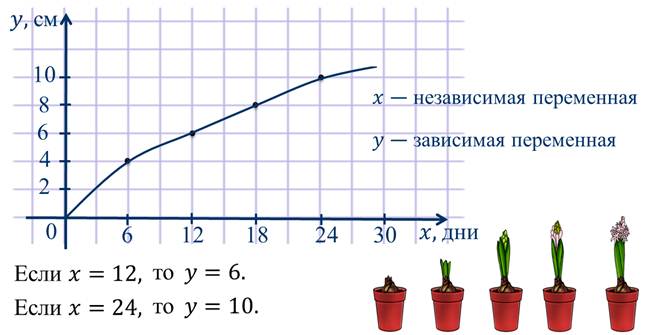
С помощью этого графика мы можем сказать, какую высоту имеет цветок в зависимости от его возраста. Например,
В данном случае икс является независимой переменной, а игрек – зависимой переменной.
Здесь зависимость одной переменной от другой также является функциональной зависимостью, или функцией. Но, в отличие от предыдущих примеров, функция задана в виде графика.
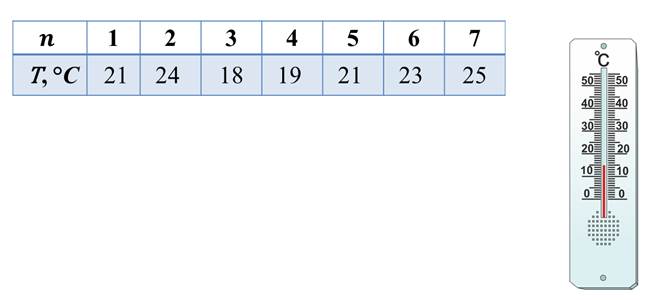
И рассмотрим таблицу, в которой представлен результат измерений средней температуры воздуха в комнате в течение недели.
В данной таблице каждому значению n (то есть номеру дня недели) соответствует значение t (температуры воздуха в комнате). Например,
Здесь каждому значению независимой переменной соответствует единственное значение зависимой переменной.
А такую зависимость мы называем функцией. В этом примере функция задана в виде таблицы.
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Понятие и основные характеристики функции
Определение функции
Представьте себе, что вы едете на машине. Через 1 час вы смотрите на карту в телефоне, и видите, что проехали 50 км. Через 2 часа, заглянув в телефон, видите, что позади уже 100 км. Сколько же вы проедете через 3 часа? Скорее всего, 150 км.
Откуда взялась эта цифра? Очевидно, из ваших выводов о скорости: наблюдения показывают, что вы едете со средней скоростью 50 км/ч, и через 3 часа преодолеете расстояние:
Если скорость известна, в эту формулу можно подставить любое время и найти соответствующее расстояние:
Такие соответствия в математике называют функциями.
Наиболее общее определение в математике:
Функция – это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.
Параметры, независимые и зависимые переменные
В примере с машиной у нас постоянная скорость v = 50 км/ч – это параметр нашей модели; параметры являются постоянными величинами.
Мы подставляем в формулу любое время t – это независимая переменная или аргумент.
И по определенному правилу получаем расстояние s(t) – это зависимая переменная или функция.
Можем дать более «узкое» и простое определение:
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Примеры
Пример 1. Запишите формулы, чтобы задать следующие функции. Укажите независимые переменные, параметры (если есть) и зависимые переменные:
а) Известна сторона квадрата a см. Чему равна площадь квадрата?
Независимая переменная: сторона квадрата a см
б) Ширина прямоугольника равна a см, длина – 5 см. Чему равен периметр прямоугольника?
Периметр прямоугольника равен: P = 2(a+5) (см)
Независимая переменная: ширина a см
Параметр: длина 5 см
Зависимая переменная: периметр P см
в) На депозит в банк положено d руб, по депозиту выплачивается 10% годовых. Сколько денег получит вкладчик в конце года?
Сумма в конце года: S = 1,1d (руб)
Независимая переменная: сумма депозита d руб
Параметр: процент 10%
Зависимая переменная: сумма к выплате S руб.
г) Машина находилась в 10 км от станции и продолжила двигаться от неё по тому же пути со скоростью 40 км/ч. На каком расстоянии от станции s (км) будет машина через t часов?
Расстояние от станции: s = 10+40t (км)
Независимая переменная: время t ч
Параметры: начальное расстояние 10 км и скорость 40 км/ч
Зависимая переменная: расстояние s км
Класс: 7
Ключевые слова: функция
Презентация к уроку
Самые простые наблюдения подчас приводят к очень важным выводам. Ход истории показал, что выводы из наблюдений за различными процессами сыграли фундаментальную роль в развитии науки и техники.
Тема «Функция» в школьной программе обширна и многогранна в своих приложениях. Эта тема является одной из важнейших для всего курса математики.Она вплотную связана с решением уравнений, неравенств, текстовых задач и др. Мы не думаем, что все выпускники школы в будущем станут математиками, но мы уверены, что будущие абитуриенты высших учебных заведенийдолжны уверенно владеть понятием функциональной зависимости, свободно строить графики функций, находить области определения и т.д. Поэтому так важно сформировать основные понятия,связанные с данной темой у семиклассников уже на первых этапах ее изучения.
В подготовке уроков мне всегда является огромным методическим подспорьем личный, систематизированный по темам, архив Приложения Математика газеты «Первое сентября». В данном случае есть целая подборка материала по теме «Функция», откуда взят материал [8]. К сожалению, некоторые статьи, из которых тоже заимствована часть материала к уроку, отксерокопированы давно без указания номера газеты или журнала и года издания.Полный список использованных источников указан в конце статьи.
Цели и задачи:
Сценарий урока (2 часа) (форма урока – ЛЕКЦИЯ с практической работой)
Техническое оснащение урока: компьютер, проектор, экран, магнитная дока.
Дидактические материалы:
Лекционная часть
Учитель: Если мы будем рисовать ряд окружностей, все более и более увеличивая радиус, то и сама окружность будет увеличиваться. Следовательно, длина окружности зависит от радиуса. В математике всякое правило, устанавливающее подобное соответствие, называется функцией.
С развитием скотоводства, земледелия, ремесел и обмена увеличилось количество известных людям зависимостей между величинами.
Мы тоже являемся функцией многих переменных, одна из которых – время. Проходят годы, и мы меняемся. Мы также зависим от своей наследственности, от книг, которые мы читаем, от температуры окружающей нас среды и от многих других факторов. И поэтому тему нашего с вами УРОКА я обозначила так:
«Что же такое функция или функции рядом с нами».
Эпиграфом предлагаю взять следующие слова:
«Математическими портретами закономерностей природы служат функции»
Презентация – 1 часть: ИСТОРИЯ РАЗВИТИЯ ПОНЯТИЯ ФУНКЦИИ (слайды 2-10)
Работа с раздаточным материалом «Что такое функция?»:
Общее определение функции, которое мы называем теперь «классическим», сформировалось в математике не очень давно – лишь в начале прошлого века. И хотя математики имели дело с различными конкретными функциями почти на каждом шагу многовекового развития науки, все же должен был быть пройден долгий путь постепенной кристаллизации элементарных понятий и их обобщений, пока ученые пришли к необходимости общего определения функции и нашли его.
Впервые в печати формулировка определения функции как аналитического выражения или «функции вообще» появилась в одной работе ученика и сотрудника Готфрида Вильгельма Лейбница, Иоганна Бернулли в 1718 году.
С проблемой общего определения функции в середине XVIII века столкнулись крупнейшие математики того времени, Жан ле Рон Даламбер и Леонард Эйлер, в решении задачи о колебаниях струны. В спор с ними ввязался молодой математик, сын Иоганна Бернулли, Даниил Бернулли. Но в их формулировках еще ничего не говорилось о допустимом характере зависимости «первых» величин от «вторых», они оставались достаточно расплывчатыми, так что каждый из последующих математиков был волен истолковывать их на свой лад. Свою лепту внесли Сильвестр Франсуа Лакруа, Жозеф Фурье, Коши, Николай Иванович Лобачевский, Петер Лежен Дирихле. Математики даже разбились на два лагеря – сторонников определения функции «по Дирихле», не требующих обязательного правила, и сторонников определения функции «по Лобачевскому», требующих обязательного правила из конечного числа слов.
В конце двадцатых годов прошлого века над определением функции возникла новая угроза, теперь уже со стороны физиков. Теория явлений в физике микромира, новая эпоха в развитии новой физики, потребовала введения нового объекта – «дельта-функции». Здесь возникли очень серьезные разногласия между физиками и математиками, и тем значительнее представляется заслуга советского математика С.Л. Соболева, который открыл класс объектов, удовлетворяющих всем выдвинутым требованиям; впоследствии они были названы «обобщенными функциями».
Последняя форма определения функции еще не означает конца ее истории. Можно не сомневаться, что в дальнейшем под воздействием новых требований как самой математики, так и других наук – физики, биологии, науки об обществе, определение функции будет изменяться и каждое следующее изменение будет открывать новые горизонты науки и приводить к важным открытиям.
Функция переменной величины есть аналитическое выражение, составленное из этой величины и постоянных. И. Бернулли, 1718.
Функция есть кривая, начертанная свободным влечением руки. Л. Эйлер, 1748.
Когда некоторые количества зависят от других таким образом, что при изменении последних изменяются и первые, то первые называются функциями вторых. Л. Эйлер, 1755.
Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних, независимо от того, известно или нет, какие операции нужно произвести, чтобы перейти от них к первому.
Функция от x есть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано и аналитическим выражением, или условием, которое подает средство испытывать все числа. Зависимость может существовать и оставаться неизвестной. Н.И. Лобачевский, 1834.
Y есть функция от x, если всякому значению x соответствует вполне определенное значение y, причем совершенно неважно, каким именно способом установлено указанное соответствие. П. Дирихле, 1837.
Презентация – 2 часть: ФУНКЦИИ РЯДОМ С НАМИ (слайды 11-19)
«Как-то проездом через некий уездный городок он узнал, что в городе есть своего рода чудо-математик. Тот решал всякую предложенную ему задачу чрезвычайно быстро, почти не думая, при помощи всего-навсего обыкновенной шахматной доски. Удивительно! Но, быть может, секрет этого доморощенного математика окажется не столь уж загадочным, если сообразить, на что похожа шахматная доска? Это та же бумага в клетку, удобная для построения графиков!»
Давайте теперь рассмотрим еще один интересный вопрос. Этот вопрос обсуждают персонажи знаменитого трактата Галилея «Беседы и математические доказательства, касающихся двух новых отраслей науки»:
«Почему не бывает животных какой угодно величины? Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций?
Ответ таков: стань слон в три раза больше, вес его бы увеличился в 27 раз, как куб размера, а площадь сечения костей и, следовательно, их прочность – только в 9 раз, как квадрат размера. Прочности костей не хватило бы выдержать увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью. Рассуждение вполне строгое и убедительное.
Строгость и убедительность ему придало знание собеседниками двух функциональных зависимостей: первая устанавливает соответствие между размерами подобных тел и их объемами – объем изменяется как куб размера; вторая связывает размеры подобных фигур и их площади – площадь изменяется как квадрат размера.
Говоря на математическом языке, линейный размер играет роль независимой переменной или аргумента, а объем и площадь являются зависимыми переменными или функциями.»
Запишем в тетради определения функции и графика функции.
Практическая часть
1. Слайд 17 «Чтобы наглядно проиллюстрировать…»
Функции рядом с нами.
Знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления. «Математическими портретами» закономерностей природы и служит функция. Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся к пословицам. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенных многовековым опытом народа.
2. Разминка (устная работа):
ТПО, стр. 30-31, № 38-39
3. Первая – вторая страница раздаточной папки (Приложение 1 и Приложение 2).
Ну, а теперь попробуем найти вот такие соответствия:
Каждой из следующих ситуаций соотнесите график функции, который описывает ее.