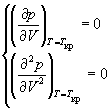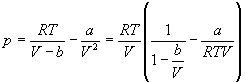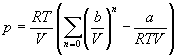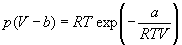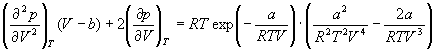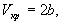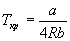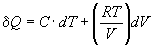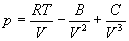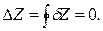что такое функции состояния системы привести примеры
Параметры и функции состояния
Наиболее значимые разделы физической и коллоидной химии
II. Химическая термодинамика как основа для понимания биоэнергетических процессов
Термодинамика – это наука, изучающая законы энергетических превращений, сопровождающих физические, химические и биохимические процессы.
Термодинамический метод является одним из самых мощных методов физической химии, позволяющим предсказывать результаты процессов.
Объектом изучения в термодинамике является система.
Система – это рассматриваемая часть материальной вселенной, отделенная от окружающей среды замкнутой поверхностью – границей. Например, системой можно назвать реакционный сосуд и гальванический элемент.
Классификация систем:
В основе классификации термодинамических систем лежат следующие признаки.
| 1) По характеру взаимодействия система – окружающая среда системы подразделяют на: | Примеры |
| Открытые — обмен со средой энергией и веществом: ∆U≠0; ∆m≠0. Закрытые –обмен только энергией и работой: ∆U≠0; ∆m=0. Изолированные – обмен веществом и энергией отсутствует: ∆U=0; ∆m=0. Абсолютно изолированных систем в природе нет. | Открытая колба с раствором, из которой может испаряться растворитель и которая может нагреваться и охлаждаться окружающей средой. Живые объекты. Плотно закрытая колба с раствором, из которой не может испариться растворитель, но она может нагреваться и охлаждаться окружающей средой. Химическая реакция, идущая в термостате. Изменение энергии при протекании химической реакции будет компенсироваться включением или выключением нагревателя, при этом общая энергия системы будет оставаться постоянной. |
2)По степени однородности системы подразделяют на: гомогенные и гетерогенные.
Систему называют гомогенной, если она состоит из одной фазы. Например, вода, воздух.
Гетерогенная система состоит из нескольких фаз, т.е. из отдельных частей. Например, лед — вода, вода — бензол, цельная кровь и т. п.
Термодинамические параметры. Состояние системы. Экстенсивные и интенсивные свойства
Состояние системы– этосовокупность параметров, характеризующих систему в данный момент времени.
Параметры и функции состояния
Параметры, которые поддаются непосредственному измерению (интенсивные свойства), называют основными параметрами состояния. Параметры состояния, которые не поддаются непосредственному измерению (внутренняя энергия, энтальпия, энтропия, термодинамические потенциалы), рассматривают как функции основных параметров состояния (функции состояния).
Параметры состояния системы разделяют на:
1) интенсивные — их значения не зависят от количества вещества; например, давление, температура, концентрация, плотность;
2) экстенсивные — их значения зависят от количества вещества (например, масса, объем, теплоемкость, внутренняя энергия, энтальпия, энтропия, термодинамические потенциалы).
Изменение параметра обозначают греческой буквой ∆ (дельта), например ∆T.
Процесс
Процесс– это переход системы из одного состояния в другое с изменением параметров состояния.
В основе классификации процессов лежат различные признаки.
1. По характеру изменения параметров состояния процессы подразделяют на:
— изотермические (Т= const, ∆T = 0);
— изобарные (р = const, ∆р = 0);
— адиабатические (теплота Q = const, ∆Q = 0);
— несамопроизвольные, или вынужденные, протекающие только при внешних энергетических воздействиях.
2. С биохимической точки зрения процессы в живых организмах подразделяют на:
— катаболические (распад и окисление энергодативных веществ в организме):
— анаболические (синтез в организме биологически важных соединений).
Термодинамический процесс вызывает энергетические изменения в системе, которые выражаются через изменение определенных величин:
— внутренней энергии (U, Дж/моль)
— энтальпии (Н, Дж или в Дж/моль)
Внутренняя энергия это весь общий запас энергиисистемы, кроме потенциальной энергии ее положения и кинетической энергии всей системы в целом.
Определение полного запаса внутренней энергии вещества невозможно, так как нельзя перевести систему в состояние, лишенное внутренней энергии (например, остановить движение электронов в атомах и молекулах). Поэтому в термодинамике рассматривают изменение (∆) внутренней энергии. Если изменение внутренней энергии конечно, то его обозначают символом ∆U (где ∆U= Uконеч.- Uнач.), а если изменение бесконечно малое – символом dU.
Теплота и работа – это форма передачи энергии либо от системы к окружающей среде, либо от окружающей среды к системе.
В отличие от внутренней энергии теплота и работа не являются функциями состояния.
Энтальпия – этоэнергия, которой обладает система, находящаяся при постоянном давлении; энтальпия численно равна сумме внутренней энергии U и потенциальной энергии pV: H=U+pV, в термодинамике оперируют величиной ∆H=Нкон.-Ннач. Изменение энтальпии ∆H в результате протекания процесса может быть выражено уравнением:
Таким образом, при р = const: Qp = ∆H; при V= const: Qv= ∆U. Поэтому энтальпия — функция состояния системы, изменение которой равно теплоте изобарного процесса; внутренняя энергия — функция состояния системы, изменение которой равно теплоте изохорного процесса.
Что такое функции состояния системы привести примеры
Глава 1. Основы химической термодинамики
1. Основные понятия термодинамики
Примеры функций состояния: энергия U, энтальпия H, энергия Гельмгольца F, энергия Гиббса G, энтропия S. Термодинамические параметры объем V, давление p, температуру T также можно считать функциями состояния, т.к. они однозначно характеризуют состояние системы. Примеры функций перехода: теплота Q и работа A.
Все выводы и соотношения термодинамики основаны на двух постулатах (исходных положениях) и трех законах (началах).
Первое исходное положение, или основной постулат термодинамики:
Любая изолированная система с течением времени приходит в равновесное состояние и самопроизвольно не может из него выйти.
Переход системы в равновесное состояние называют релаксацией. Основной постулат термодинамики ничего не говорит о времени релаксации. В классической равновесной термодинамике вообще нет времени. Термодинамика позволяет установить только возможность протекания процессов, но не может определить скорость этих процессов.
Второе исходное положение, или нулевой закон термодинамики описывает свойства систем, находящихся в состоянии теплового равновесия:
Если система А находится в тепловом равновесии с системой В, а та, в свою очередь, находится в равновесии с системой С, то системы А и С также находятся в тепловом равновесии.
Из нулевого закона следует, что при равновесии внутренние параметры системы являются функциями внешних параметров и температуры. Уравнение, связывающее внутренние параметры с внешними параметрами и с температурой, называют уравнением состояния термодинамической системы. В общем случае уравнение состояния имеет вид:
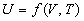
Если известны термическое и калорическое уравнения состояния, то с помощью законов термодинамики можно определить все термодинамические свойства системы, т.е. получить ее полное термодинамическое описание. Сами уравнения состояния нельзя вывести методами классической термодинамики, но их можно определить экспериментально.
Для описания реальных газов, в которых частицы имеют конечные размеры и взаимодействуют друг с другом, используют более сложные уравнения состояния:
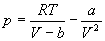
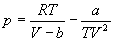
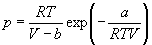
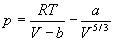
С высокой точностью поведение любого реального газа можно описать с помощью вириального разложения по степеням обратного объема:
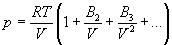
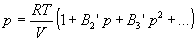
Уравнение состояния идеального газа и вириальное уравнение состояния реального газа можно вывести методами статистической термодинамики.
Иногда уравнения состояния реальных газов записывают через так называемые приведенные переменные, которые определяют через параметры критического состояния газов: pr = p / pкр, Vr = V / Vкр, Tr = T / Tкр, где критические параметры определяются как координаты точки перегиба на изотерме реального газа:
ПРИМЕРЫ
Пример 1-1. Докажите, что при больших объемах уравнение Ван-дер-Ваальса переходит в уравнение идеального газа.
Решение. Уравнение Ван-дер-Ваальса:
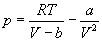
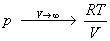
Пример 1-2. Найдите вириальные коэффициенты Bi для газа, подчиняющегося уравнению Ван-дер-Ваальса.
Решение. В уравнении Ван-дер-Ваальса выделим сомножитель RT/V:
Если разложить первое слагаемое в скобке в ряд по степеням b/V, получим:
Из этого разложения следует, что второй вириальный коэффициент газа Ван-дер-Ваальса зависит от температуры:
Пример 1-3. Найдите критические параметры и приведенное уравнение состояния для газа Дитеричи (I уравнение).
Решение. Запишем уравнение Дитеричи в виде:
и продифференцируем левую и правую часть этого уравнения два раза по объему при постоянной температуре:
и учтем, что в критической точке первая и вторая производная равны 0:
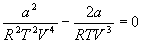
откуда находим: 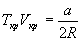
Если продифференцировать обе части уравнения состояния по объему один раз с учетом равенства нулю первой производной, то можно найти второе соотношение между критическими объемом и температурой:
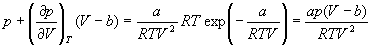
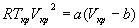
Подставляя сюда первое найденное соотношение для критических параметров, получим:
И, наконец, подставляя эти параметры в уравнение состояния, находим критическое давление:
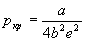
Для вывода приведенного уравнения состояния подставим в уравнение Дитеричи приведенные переменные:
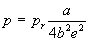
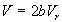
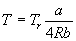
В результате получаем приведенное уравнение Дитеричи, не содержащее индивидуальных параметров:
ЗАДАЧИ
1-1. Приведите пример термодинамического процесса, который может совершаться как обратимо, так и необратимо. Назовите для этого процесса по одной функции состояния и перехода.
1-2. Приведите примеры систем со временем релаксации порядка: а) секунд; б) часов; в) десятилетий.
1-3. Изменение теплоты в зависимости от температуры и объема в некоторой системе описывается уравнением:
1-4. Докажите, что при больших объемах первое уравнение Дитеричи переходит в уравнение идеального газа.
1-5. Найдите частные производные 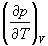
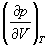
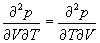
1-6. Используя вириальные разложения (1.4) и (1.5), найдите связь между вириальными коэффициентами B2, B3 и B2‘, B3‘.
1-7. Найдите критические параметры и приведенные уравнения состояния для газов: а) Ван-дер-Ваальса; б) Бертло.
1-8. Предложено следующее уравнение состояния (для одного моля):
Выразите критические параметры через постоянные B и C и найдите фактор сжимаемости PV/RT в критической точке.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Функции состояния
При изучении изменения свойств системы в процессе используется метод функций. Различают функции состояния и функции перехода (процесса).
Функции состояния– функции независимых параметров, определяющих равновесное состояние термодинамической системы, т.е. это величины, не зависящие от предыстории системы и полностью определяемые ее состоянием в данный момент. Изменение термодинамических функций состояния в процессе перехода от начального состояния (1) до конечного состояния (2) не зависит от пути (характера процесса), а определяется только разностью значений данной функции в конечном и начальном состоянии.
Например, давление газа – однозначная функция объема и температуры. В то же время работа может зависеть от пути перехода системы в конечное состояние, поэтому она является функцией процесса, а не состояния.
Другими словами, если Ф – функция состояния, то
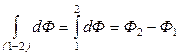
Функциями состояния являются внутренняя энергия, энтальпия, энтропия, энергия Гиббса, энергия Гельмгольца и др. Поскольку изменение функции состояния не зависит от пути перехода, то бесконечно малое изменение функции состояния является полным дифференциалом.
Полный дифференциал функции нескольких переменных 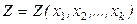
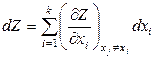
Термодинамические функции чаще рассматриваются как функции двух переменных 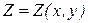
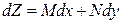
При рассмотрении соотношений вида (1.2) самым важным будет установить, является ли полным дифференциал функции Z.
Если dZ – полный дифференциал, то величина изменения функции Z при переходе из состояния (1) в состояние (2) равно разности значений функции Z в этих состояниях:
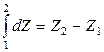
Если dZ не является полным дифференциалом, то величина изменения функции Z при переходе из состояния (1) в состояние (2) будет различной в зависимости от того, по какому пути осуществляется переход. Функции, величина изменения которых зависит от пути процесса, называются функциями процесса (теплота, работа).
Далее, если dZ = Mdx + Ndy является полным дифференциалом, то
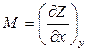
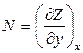
Тогда в соответствии с теоремой Бернули-Эйлера для функции Z = Z(x,y) значение ее второй производной не зависит от порядка дифференцирования
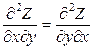
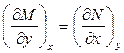
Таким образом, если для дифференциального соотношения типа (1.2) выполняется соотношение (1.4), то дифференциал dZ является полным дифференциалом, а функция Z является функцией состояния.
Если же условие (1.4) не выполняется, то в уравнении (1.2) dZ не является полным дифференциалом, а функция Z будет функцией процесса. Следует иметь в виду, что для дифференциала функции процесса dZ можно найти такую функцию λ(x,y), умножением на которую дифференциал функции процесса dZ превращается в полный дифференциал функции состояния R(x,y):
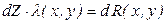
Такую функцию λ(х,y) называют интегрирующим множителем. (Например, величина 1/T является интегрирующим множителем для dQ, где Q – теплота (функция процесса), а dS = dQ/T – полный дифференциал функции состояния энтропии).
Следует отметить также, что Z является функцией состояния, если в круговом (циклическом) процессе ее изменение равно нулю:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметры состояния системы



I. Основные понятия термодинамики
Тема : Термодинамика химического равновесия.
Цель лекции : изучение вопросов по термодинамике химического равновесия
План:
Содержание лекции:
Химическая термодинамика – это раздел физической химии, изучающий взаимопревращение теплоты и энергии при протекании химической реакции.
Термодинамика основана на ряде понятий: система, состояние системы, параметры состояния системы, функции состояния системы, внутренняя энергия системы и т. д.
Термодинамическая система – это тело или группа тел, взаимодействующих между собой, и отделённых от окружающей среды реальной или воображаемой поверхностью раздела.
Изолированная система – это система, которая не обменивается с окружающей средой ни веществом, ни энергией.
Закрытая система – это система, которая не обменивается со средой веществом, но обменивается энергией.
Открытая система – это система, которая обменивается со средой и веществом, и энергией.
Примером открытой системы является живая клетка.
Состояние системы – это набор свойств системы, позволяющих описать систему с точки зрения термодинамики.
Например, для оценки состояния человеческого организма, как термодинамической системы, врач должен оценить некоторые его свойства (температура, давление, концентрация биологических жидкостей).
Физические свойства, характеризующие состояние системы, называют параметрами состояния системы.
Взаимодействие системы с окружающей средой заметно по изменению параметров системы.
Экстенсивные параметры – это параметры, которые зависят от количества вещества системы и суммируются при объединении систем (объём, масса, энергия, площадь и т.д.).
Интенсивные параметры – это параметры, которые не зависят от количества вещества и выравниваются при объединении систем (температура, давление, концентрация, плотность, поверхностное натяжение).
Параметры состояния связаны уравнением состояния.
Переход системы из одного состояния в другое с изменением хотя бы одного параметра называется термодинамическим процессом.
Внутренняя энергия является одной из таких функций.
В XIX веке немецкий судовой врач Майер Ю.Р. и английский ученый Джоуль Д. показали, что теплота и работа способны к взаимопревращениям, являясь разными способами передачи энергии.
Наблюдая за людьми в разных климатических зонах, Майер сделал вывод, что теплота сгорания пищи используется на поддержание постоянной температуры тела и на выполнение мускульной работы. Это наблюдение легло в основу 1 закона термодинамики.