что такое формула герона
Формула Герона
Фо́рмула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, b, c:
где p — полупериметр треугольника: 
.
где 
— угол треугольника, противолежащий стороне 
. По теореме косинусов:
.
Замечая, что 
, 
, 
, 
, получаем:
История
Эта формула содержится в «Метрике» Герона Александрийского (I века н. э.) и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник.
Вариации и обобщения
См. также
Полезное
Смотреть что такое «Формула Герона» в других словарях:
Итерационная формула Герона — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка… … Википедия
ГЕРОНА ФОРМУЛА — выражает площадь S треугольника через длины трех его сторон a, b и c и полупериметр P = (a + b + c)/2Названа по имени Герона Александрийского … Большой Энциклопедический словарь
Герона формула — формула выражающая площадь треугольника через три его стороны. Именно, если а, b, с длины сторон треугольника, a S его площадь, то Г. ф. имеет вид: где через р обозначен полупериметр треугольника Г. ф.… … Большая советская энциклопедия
ГЕРОНА ФОРМУЛА — формула, выражающая площадь треугольника через его стороны a, b, с: где Названа по имени Герона (ок. 1 в. Н. Э.), А. Б. Иванов … Математическая энциклопедия
ГЕРОНА ФОРМУЛА — выражает площадь 5 треугольника через длины трёх его сторон а, b и с и полупериметр р = (а + b + с)/2: s = кв. корень p(p a)(p b)(p c). Названа по имени Герона Александрийского … Естествознание. Энциклопедический словарь
Герона формула — … Википедия
Герон — Александрийский Ήρων ο Αλεξανδρεύς Научная сфера: механика … Википедия
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Формула Герона.
Формула Герона позволяет определить площадь треугольника (S) из его сторон a, b, c.
Чтобы вычислить площадь треугольника ∆ABC, если известны длины его сторон a, b и c, используют формулу Герона:
где p — полупериметр треугольника:
.
Рассмотрим нахождение площади треугольника с помощью формулы Герона:
Есть треугольник со сторонами a = 5, b = 6, c = 7. Вычислим полупериметр:
Далее подставляем данные в формулу для определения площади:
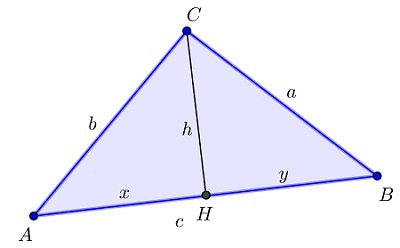
Формула Герона, доказательство.
В нем: CH — высота треугольника ABC, которая проведена из вершины C, |CH|=h, |AH|=x, |BH|=y.
Тогда c=x+y, и из теоремы Пифагора из треугольников ACH и BCH имеем:
Учитывая, что x+y=c, получаем 
и 
.
Складываем последнее равенство с равенством y+x=c, получаем:
Далее находим высоту h треугольника:
Подставляем эти выражения в определенное выражение для h 2 :
Учитываем то, что 
, получаем требуемое.
Что можно вычислить по формуле Герона
Формула Герона
Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.
Формулировка теоремы Герона
Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.
Формула и доказательство
Формула Герона выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.
Чтобы вычислять полупериметр, нужно пользоваться формулой:
Приведем доказательство.
Для этого рассмотрим треугольник ABC.
CH – высота треугольника.
По теореме Пифагора из треугольников ACH и BCH получаем:
Найдем высоту треугольника.
С помощью этих равенств найдем высоту.
Для каких треугольников действует теорема
Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.
Примеры решения задач
Задача 1
Рассчитать площадь треугольника, если a=6, b=8, c=6.
Решение
Тогда площадь треугольника равна:
Задача 2
Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.
Решение
Диагонали AC и BD пересекаются в точке O.
Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.
Задача 3
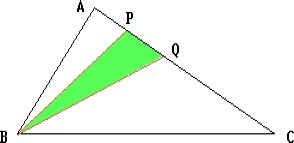
В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.
Решение
BP и BQ – высота и биссектриса треугольника.
По свойству биссектрисы треугольника:
По теореме Пифагора из треугольника APB получаем:
Следовательно, \(PQ = AQ – AP = 13 – 10 = 3\)
Формула Герона для треугольника
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
Формула площади
Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).
Полупериметр ( p ) вычисляется таким образом:
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.
Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Формула Герона для площади треугольника
Треугольник – это фигура, которая образуется после соединения трех точек, не лежащих на одной прямой отрезками. 
Точки называются вершинами, а отрезки сторонами. Для расчета треугольника существует множество формул, которые помогают найти как длины сторон, радиусы углов и прочие составляющие фигуры, так и площадь треугольника.
Самой распространенной формулой для расчета площади треугольника по трем сторонам является формула Герона 
. Если известны длины всех сторон, то можно вычислить площадь фигуры, применив формулу Герона для площади треугольника.
| Сторона a= | Сторона b= | Сторона c= |
| Ответ: Площадь треугольника = 6.000 | ||
Три окружности с радиусами 6, 7, 8 внешне попарно касаются друг друга. Найти площадь треугольника, образованного центрами этих окружностей. Посмотреть решение
училась в школе шесть десятков лет назад, геометрию забыла, но в связи с тем, что мебель из ДСП смешно ставить в сантехническую кабину (недолговечна), а из дерева и красивая пока недоступна. На сайтах гостиниц Бахрейна очень понравилась, примерно в похожем стиле хочу сделать сама угловой шкаф в ванную, но чтобы закупить материалы, надо начертить детали и посчитать объем и без геометрии здесь не обойтись. Поэтому я благодарна Вам за теорему Пифагора, за древнеиндийских математиков, за тригонометрические формулы и за калькуляторы расчетов. С искренним уважением Нина Ивановна!
Вбиваем стороны 2,3,5 и вуаля:
Ответ: Площадь треугольника = 0.000
Каждая сторона должна быть меньше суммы двух других. 5>2+3?!
Это не треугольник, это 3 точки на одной прямой
Стороны: 3,4,7 и оппа!
Ответ: Площадь треугольника = 0.000
Потому что у треугольника со сторонами 3, 4 и 7 площадь таки будет 0. 3+4=7. Треугольник вырождается в отрезок.
Нет, по теории, любой треугольник можно назвать таковым, если сумма двух сторон его больше или равна оставшейся стороны.
Например:
стороны 10 25 30, следует что это треугольник так как
(10+25)>30
(10+30)>25
(30+25)>10
Ответ: сумма любых 2-х сторон треугольника > 3-й стороны. А у Вас получается 3,…+3,…
Господа, неравенство треугольника ещё никто не отменял. Поэтому, прежде чем вычислять площадь треугольника, проверяют его существование, используя неравенство треугольника.