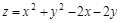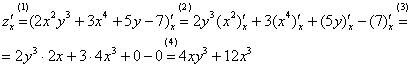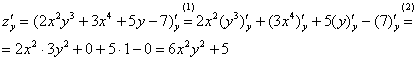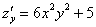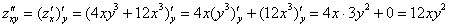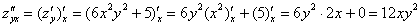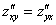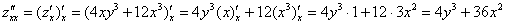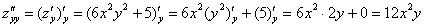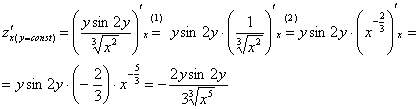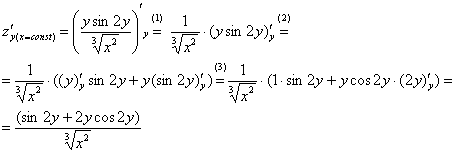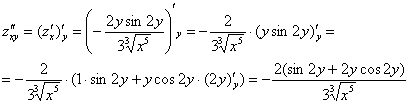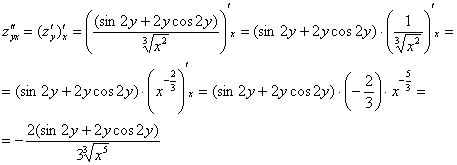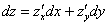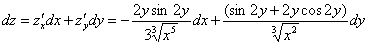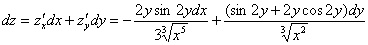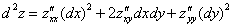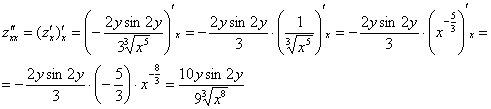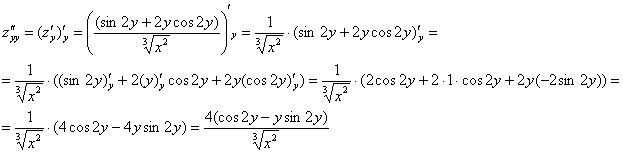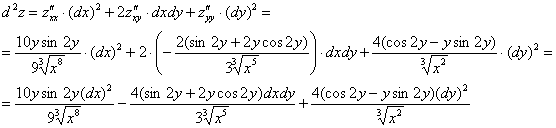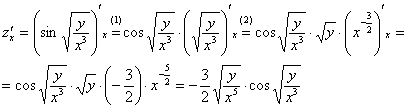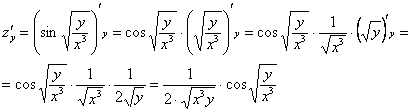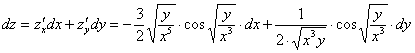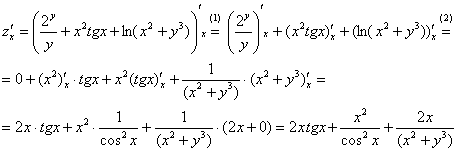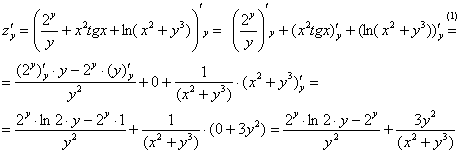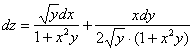что такое фнп в математике
Электронная библиотека
Определение: Переменная величина z называется однозначной функцией двух переменных х и у, если каждой точке (х, у), принадлежащей некоторому множеству D, соответствует одно определенное значение величины z.
Определение. Переменные х и у называются независимыми переменными или аргументами.
Определение Множество D называется областью определения функции.
Область определения функции в простейших случаях представляет собой некоторое множество D точек плоскости Оху.
Геометрическим изображением функции z = f(х, у) (графиком) является некоторая поверхность.
Аналогично определяется функция любого числа переменных.
Пусть D – произвольное множество точек n-мерного арифметического пространства.
Если каждой точке Р(x1, x2, …, xn), принадлежащей области D поставлено в соответствие единственное значение переменной z, то z называют функцией n переменных:
Линией уровня функции двух переменных z = f(x, y) называется линия плоскости Оху, в точках которой функция сохраняет постоянное значение f(x, y) = С.
Поверхностью уровня функции трех переменных u = f(x, y, z) называется поверхность f(x, y, z) = С, в точках которой функция сохраняет постоянное значение.
Пример 1.1. Найти область определения функции z = arcsin(x/y 2 ).
Областью определения функции является часть плоскости, заключенная между двумя параболами у 2 = х и у 2 = –х, за исключением точки О(0,0) (рис 1.1).
Рис. 1.1. Область определения функции z = arcsin(x/y 2 )
Пример 1.2. Найти область определения функции
когда R 2 – х 2 – у 2 – z 2 0; а выражение
существует, если х 2 + у 2 + z 2 – r 2 > 0.
Из неравенства х 2 + у 2 + z 2 – r 2 > 0 имеем
Решение. Уравнение семейства линий уровня имеет вид
Придавая С различные вещественные значения, получим концентрические окружности с центрами в начале координат.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Функции нескольких переменных
Вы будете перенаправлены на Автор24
Функция двух переменных
Частным случаем функции многих переменных является функция двух переменных.
Функция двух переменных может быть задана двумя способами:
Определить и изобразить область определения функции
Решение:
Линия, которая ограничивает область определения на плоскости, называется границей области.
Точки области, которые не лежат на границе, называются внутренними точками данной области.
Если область состоит только из внутренних точек (не содержит граничных точек), то она называется открытой (незамкнутой).
Готовые работы на аналогичную тему
Определить и изобразить область определения функции
Решение:
Область определения является открытой, т.е. незамкнутой.
Если область содержит и внутренние точки, и граничные точки, то она называется закрытой (замкнутой).
Определить и изобразить область определения функции
Решение:
Область определения является закрытой, т.е. замкнутой.
Понятие функции нескольких переменных не ограничивается рассмотрением только функции двух переменных. Данное понятие легко обобщается на количество переменных от трех и более.
Понятие области определения для функции трех и более переменных вводится аналогично соответствующему определению понятия для функции двух переменных.
Графическое изображение функции двух переменных
Функцию двух переменных можно изобразить в пространстве с помощью графика.
Множество точек графика функции двух переменных образует некоторую поверхность.
Изобразить график функции
Решение:
В пространстве невозможно изобразить с помощью графика функции трех и более переменных.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 03 2021
Основные понятия ФНП
Функции нескольких переменных
Определение. Пусть имеется n переменных величин, и каждому набору их значений 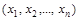
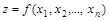
Переменные 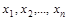
Пример 1. Производственная функция Кобба-Дугласа 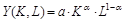
В дальнейшем будем рассматривать функции двух переменных. Область определения X такой функции есть подмножество координатной плоскости Oxy.
Определение. Окрестностью точки 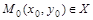
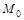
Круг на плоскости есть двумерный аналог интервала на прямой.
Графиком функции двух переменных 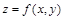
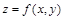
Определение. Линией уровня функции нескольких переменных 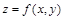
Таким образом, линии уровня – это семейство непересекающихся кривых, описываемое уравнениями вида
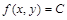 | (1) |
Обычно берут арифметическую прогрессию чисел C с постоянной разностью h.Тогда там, где функция изменяется быстрее, линии уровня располагаются ближе друг к другу.
Пример 2. Найти линии уровня функции
Решение: Линии уровня – это семейство кривых, описываемых уравнением:
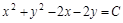
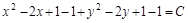
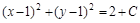
Это уравнение описывает семейство окружностей с центром в точке (1;1) радиуса 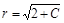
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Частные производные функции двух переменных.
Понятие и примеры решений
На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.
Для эффективного изучения нижеизложенного материала вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на странице Математические формулы и таблицы.
Быстренько повторим понятие функции двух переменных, я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как 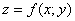
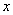
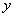
Пример: 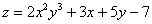
Иногда используют запись 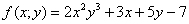
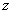
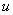
С геометрической точки зрения функция двух переменных 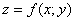
никогда не давал списывать мой вузовский преподаватель является моим «коньком».
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:
…да, кстати, для этой темы я таки создал маленькую pdf-книжку, которая позволит «набить руку» буквально за пару часов. Но, пользуясь сайтом, вы, безусловно, тоже получите результат – только может чуть медленнее:
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения:
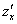
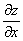
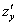
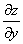
Начнем с 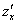
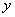
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без 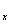
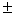
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования 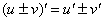
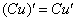
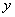
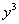
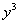
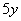
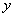
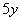
(3) Используем табличные производные 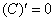
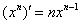
(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.
Теперь 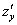
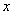
(1) Используем те же правила дифференцирования 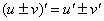
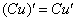
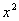
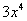
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для 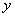
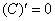
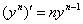
В чём смысл частных производных?
По своей сути частные производные 1-го порядка напоминают «обычную» производную:
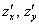
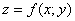
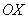
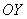
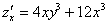
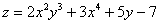
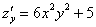
! Примечание: здесь подразумеваются направления, которые параллельны координатным осям.
В целях лучшего понимания рассмотрим конкретную точку 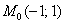
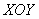
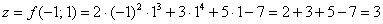
Вычислим частную производную по «икс» в данной точке:
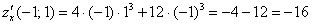
Отрицательный знак «иксовой» производной сообщает нам об убывании функции 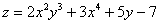
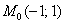
Теперь узнаем характер «местности» по направлению оси ординат: 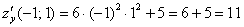
Производная по «игрек» положительна, следовательно, в точке 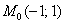
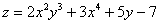
Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше по модулю – тем поверхность круче, и наоборот, чем оно ближе к нулю – тем поверхность более пологая. Так, в нашем примере «склон» по направлению оси абсцисс более крут, чем «гора» в направлении оси ординат.
Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности 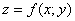
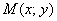
Систематизируем элементарные прикладные правила:
1) Когда мы дифференцируем по 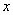
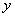
2) Когда же дифференцирование осуществляется по 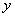
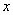
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (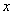
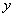
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
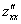
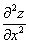
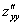
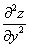
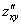
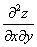
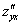
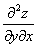
Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.
Для удобства я перепишу уже найденные частные производные первого порядка: 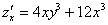
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную 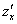
Аналогично:
В практических примерах можно ориентироваться на следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс».
Никаких изобретений, берем 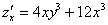
Аналогично:
Следует отметить, что при нахождении 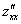
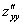
Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных. Но всему своё время:
Вычислить частные производные первого порядка функции 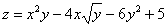
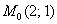
Это пример для самостоятельного решения (ответы в конце урока). Если возникли трудности с дифференцированием корней, вернитесь к уроку Как найти производную? А вообще, довольно скоро вы научитесь находить подобные производные «с лёту».
Набиваем руку на более сложных примерах:
Найти частные производные первого порядка функции 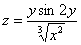
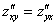
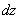
Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: 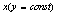
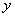
(1) Выносим все константы за знак производной. В данном случае 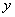
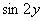
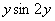
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является 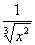
(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения 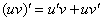
(3) Не забываем, что 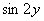
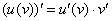
Теперь находим смешанные производные второго порядка:
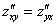
Запишем полный дифференциал 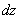
Полный дифференциал первого порядка функции двух переменных имеет вид:
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов 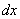
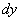
И по неоднократным просьбам читателей, полный дифференциал второго порядка.
ВНИМАТЕЛЬНО найдём «однобуквенные» производные 2-го порядка:
и запишем «монстра», аккуратно «прикрепив» квадраты 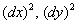
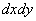
Ничего страшного, если что-то показалось трудным, к производным всегда можно вернуться позже, после того, как поднимите технику дифференцирования:
Найти частные производные первого порядка функции 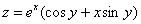
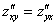
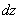
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров со сложными функциями:
Найти частные производные первого порядка функции 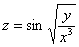
Записать полный дифференциал 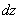
Решение:
(1) Применяем правило дифференцирования сложной функции 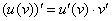
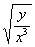
(2) Здесь используем свойство корней: 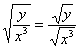
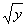
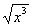
Аналогично:
Запишем полный дифференциал первого порядка:
Найти частные производные первого порядка функции 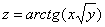
Записать полный дифференциал 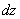
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Найти частные производные первого порядка функции 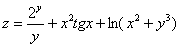
(1) Используем правило дифференцирования суммы
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении 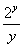
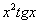
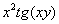
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: 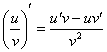
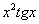
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Найти частные производные первого порядка функции 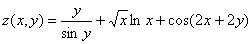
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.
Дана функция двух переменных 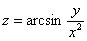
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Что дальше? Дальше знакомимся с родственной темой – частными производными функции трёх переменных. После этого я рекомендую ДОБРОСОВЕСТНО (жить будет легче ;)) отработать технику дифференцирования на уроках Производные сложных функций нескольких переменных, Как проверить, удовлетворяет ли функция уравнению? и Частные производные неявно заданной функции. И, наконец, обещанная вкусняшка – Производная по направлению и градиент функции. Стратегия и тактика знакомы – сначала учимся решать, затем вникаем в суть!
Пример 2: 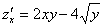
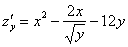
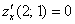
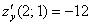
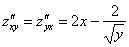
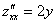
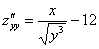
Пример 4: Ссылка для просмотра или скачивания ниже.
Пример 6: 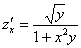
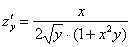
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5