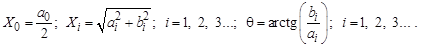что такое физический процесс
Физических процессов



Бийский технологический институт (филиал)
государственного образовательного учреждения
высшего профессионального образования
«Алтайский государственный технический университет
Р.Г. Гареева
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
В ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
Издательство Алтайского государственного технического
университета им. И.И. Ползунова
Внимание.
Для студентов заочного отделения необязательными для сдачи являются следующие разделы: 2.7-2.9, 3.
СОДЕРЖАНИЕ
| 1 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФИЗИЧЕСКИХ ПРОЦЕССОВ………………………………………………..………. |
| 1.1 Классификация детерминированных процессов…………… |
| 1.2 Классификация случайных процессов….……………………. |
| 1.3Основные статистические характеристики стационарных случайных процессов………………………………………………. |
| 1.4 Контрольные вопросы………………………………………… |
| Литература………………………………………………………… |
| 2 СИСТЕМЫ С ОДНИМ ВХОДОМ И ОДНИМ ВЫХОДОМ…….. |
| 2.1 Свойства идеальной системы…………………………. ……. |
| 2.2 Частотные характеристики…………………………………… |
| 2.3 Спектральный анализ идеальной системы. ………………… |
| 2.4 Функция обычной когерентности…………………………….. |
| 2.5 Система с внешним шумом на выходе……………….……… |
| 2.6 Система с внешним шумом на входе………………………… |
| 2.7 Влияние внешнего шума……………………………………… |
| 2.8 Система с обратной связью…………………………………… |
| 2.9 Использование зондирующего сигнала……………………… |
| 2.10 Контрольные вопросы……..………………………………… |
| Литература………………………………………………………… |
| 3 СИСТЕМЫ С ОДНИМ ВХОДОМ И НЕСКОЛЬКИМИ ВЫХОДАМИ………………………………………………………… |
| 3.1 Спектральные соотношения………………………………….. |
| 3.2 Оценивание относительного запаздывания………………… |
| 3.3 Локализация неизвестного источника……………………….. |
| 3.4 Контрольные вопросы……………..…………………………. |
| Литература………………………………………………………… |
Основные Характеристики
физических процессов
Все наблюдаемые процессы, характеризующие физические явления, можно классифицировать как детерминированные и недетерминированные.
К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями.
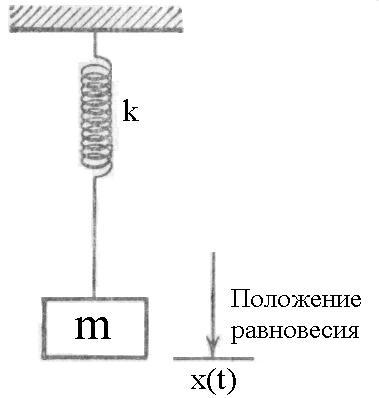
Рассмотрим, например, твердое тело, подвешенное к неподвижной основе на упругой пружине с нулевой массой (рисунок 1.1).
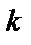
Рисунок 1.1 – Тело, подвешенное на пружине
Предположим, что тело получает начальное смещение 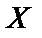
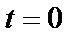
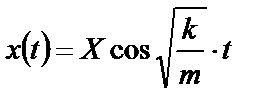
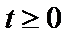
где 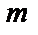
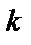
Формула (1.1) точно описывает положение тела в любой момент времени в будущем. Следовательно, физический процесс, характеризующий движение тела, относится к детерминированным процессам.
На практике встречается много физических явлений, которые с высокой степенью приближения могут быть описаны точными математическими соотношениями (движение спутника по околоземной орбите, изменение температуры воды при нагревании).
Однако можно назвать множество других физических процессов, имеющих недетерминированный характер (изменение высоты волн на поверхности моря, изменение напряжения на выходе генератора шума). Точное значение таких процессов в некоторый момент времени в будущем предсказать невозможно. Эти процессы случайны по своей природе.
Случайные (стохастические или недетерминированные) процессы не могут быть описаны точными математическими соотношениями, для их описания требуются усредненные статистические характеристики.
Во многих случаях трудно решить, относится ли рассматриваемый процесс к детерминированным или к случайным. Можно утверждать, что в действительности ни один физический процесс нельзя считать строго детерминированным, поскольку всегда существует возможность того, что в будущем какое-либо непредвиденное событие изменит течение процесса таким образом, что полученные данные будут носить совершенно иной характер, чем предполагалось ранее. С другой стороны, можно полагать, что в действительности ни один физический процесс не имеет строго случайной природы, так как при условии достаточно полного знания механизма изучаемого процесса его можно описать точными математическими соотношениями.
Практическое решение о детерминированном или случайном характере процесса обычно принимается исходя из возможности или не возможности его воспроизведения при заданных условиях. Если многократное повторение опыта дает одинаковые результаты (с точностью до ошибки измерения), то процесс считают детерминированный. Если же повторение опыта в идентичных условиях приводит к различным исходам, природа процесса полагается случайной.
Представление физических процессов
Математическое представление модели физического процесса в виде формул. Изобретение и применение формулы гравитационного взаимодействия. Классификация коррозионных сред, разрушений и процессов. Причины и механизм возникновения электрохимической коррозии.
| Рубрика | Физика и энергетика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 08.04.2015 |
| Размер файла | 87,3 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Вот несколько неординарных примеров, когда процесс и объект не наблюдаемый, но зато регистрируемый и пример, когда процесса нет.
1. Вопрос о существовании объектов «чёрная дыра». Объект «чёрная дыра» не наблюдаемый, но зато регистрируемый. О его конкретном расположении указывают светящиеся звёзды, которые связаны с ним гравитационным взаимодействием и обращаются вокруг него.
2. Вопрос о существовании нейтрино. Все реакции синтеза связаны с излучением обменных частиц фотонов и нейтрино. И, наоборот, при реакции распада именно такие же частицы должны быть поглощены. Если фотоны можно зарегистрировать и замерить, то нейтрино замерить нельзя, но можно зарегистрировать через дефект массы (энергию связи). Дефект массы указывает о наличии и материальности существовании нейтрино.
Если процесс наблюдаемый и регистрируемый, тогда учёные представляют модель процесса математически в виде формул. Модель (формула) должна описывать закономерности, участвующих в этих процессах тел или частиц. Модель должна быть взаимосвязана с другими процессами и не противоречить другим процессам. При анализе процессов должны соблюдаться научная методология, причинно-следственная связь и логическая последовательность. В результате анализа процесса учёные получают основную формулу описывающую данный процесс.
Всё ли в этих формулах близко к реальности? Нет ли там ошибок или даже фальсификаций?
Рассмотрим, как получаются формулы.
Во-первых, необходимо наличие самого наблюдаемого или регистрируемого физического процесса с объектом, а не какие-то фантазии типа сокращается пространство, но увидеть это невозможно и померить тоже.
Во-вторых, необходим эксперимент или модель процесса, в которой выявлены закономерности и все параметры физических величин, связанных между собой.
Рассмотрим несколько разных вариантов формул основных физических процессов в природе.
1. Формула гравитационного взаимодействия
В последствии коэффициент пропорциональности вычислили в результате эксперимента.
Этим экспериментом подтвердился закон открытый Ньютоном и формула стала
Коэффициент пропорциональности обязан согласовать размерности левой и правой частей уравнения, а также содержать в себе единичную силу взаимодействия, являющуюся показанием динамометра или устройства его заменяющего.
Но коэффициент пропорциональности как единичная сила не был экспериментально вычислен.
Тогда ещё не знали как измерять электрические заряды.
В такой же ситуации оказался и Ампер. В 1820г.
Но коэффициент пропорциональности как единичная сила не был экспериментально вычислен.
Пользоваться этими формулами было невозможно.
Необходимы были эксперименты по вычислению коэффициентов пропорциональности, которые являются единичными силами взаимодействий.
Эти коэффициенты вычислены один через другой и скорость света. Но теоретически придумывать коэффициенты пропорциональности к формулам силовых взаимодействий нельзя, они должны вычисляться обязательно в результате эксперимента и только по динамометру или устройству его заменяющего.
Однако нет экспериментов, нет и коэффициентов. Необходимо дождаться проведения экспериментов по определению коэффициентов пропорциональности (единичные силы взаимодействия или электрическая и магнитная постоянные) в формулах Кулона и Ампера.
И второй случай, когда Максвелл без эксперимента «вывел» (п
3. Рассмотрим формулу гипотезы Планка о связи частоты и энергии фотона.
Эту формулу экспериментально подтвердить невозможно и, естественно, коэффициент пропорциональности неизвестен. Планк вместо экспериментально полученного коэффициента подбирает на его место что-нибудь из того, что имеется в других формулах. Но те формулы связаны только с конкретным диапазоном электромагнитного излучения, а формула предназначена для всех частотных диапазонов. Каков физический смысл этого коэффициента? На этот вопрос ответа нет. Кроме того, этот коэффициент, который назвали постоянная Планка, не является минимальным квантом (порцией энергии) в природе. Минимальным квантом в природе является энергия теряемая фотоном за одно колебание фотона. Энергия одного колебания фотона всегда величина постоянная и не от чего не зависящая. Естественно, что потеря энергии за одно колебание очень незначительная величина, поэтому поиски и расчёты её необходимо производить за как можно большее время полёта фотона (расстояние).
Для массы частицы получим
Задаваясь количественными значениями параметров, можно получить оценочные значения потерь фотона при одном колебании
Вот эти величины уже имеют физический смысл и статус как минимальные кванты в природе.
Однако, необходимо помнить, что формула гипотезы Планка, не имеющая экспериментального подтверждения, не может участвовать в доказательствах других процессов. А численные значения, полученные с использованием постоянной Планка, чисто условные, только сохраняющие пропорциональность исчисления. Вероятно, что заложенная ошибочность в коэффициенте постоянная Планка всё же, где-то проявится, и нужно быть внимательным, чтобы этот момент не пропустить.
4.О коэффициентах пропорциональности в формулах СТО Эйнштейна.
2. Классификация коррозионных сред, разрушений и процессов. Показатели скорости коррозии
Коррозия сопровождается выделением энергии (процессы коррозии протекают самопроизвольно и сопровождаются убылью энергии Гиббса (? G n +
Гетерогенный процесс состоит из последовательно протекающих стадий:
— диффузии частиц окислителя к поверхности металла,
— их адсорбции на ней,
— поверхностной химической реакции (в результате которой происходит окисление металла),
— десорбции продуктов с поверхности, их переноса в объем коррозионной среды.
Скорость коррозии определяется скоростью наиболее медленной (лимитирующей) в данных условиях стадии, которая может иметь как химическую (окисление металла), так и физическую (диффузия электролита или газа) природу.
Наиболее часто для характеристики скорости коррозии используют показатель убыли массыи глубинный показатель.
Показатель убыли массы rмасс. указывает потерю массы в единицу времени? с единицы поверхности S испытуемого образца:
В справочной литературе r глуб. обычно приводится в мм/год.
3. Химическая коррозия: виды и разновидности
2. Химическую газовую коррозию (в дальнейшем газовую), протекающую обычно при высоких температурах.
Эти два вида химической коррозии не сопровождаются возникновением электрического тока, т.е. представляют собой обычное окислительно-восстановительное (химическое) взаимодействие металла с окружающей средой.
Газовая коррозия является наиболее часто встречающимся видом химической коррозии и обычно протекает при высоких температурах в газах и парах агрессивных веществ, когда исключена возможность их конденсации на поверхности металла, поэтому ее называютвысокотемпературной коррозией. Это коррозия сопел ракетных двигателей, лопаток газовых турбин, элементов электронагревателей и др. К газовым коррозионным агентам относятся О2, СО2, SO2, H2O, H2S, Cl2. Их агрессивность по отношению к различным металлам не является одинаковой, следовательно, и скорость коррозии различается.
Рассмотрим пример наиболее часто встречающейся на практике газовой коррозии:—коррозия железа, чугуна и сталей в атмосфере О2,, СО2, и H2O:
При нагревании этих материалов происходит их окисление:
Состав продуктов окисления определяется главным образом температурой газовой коррозионной среды.
При этом ухудшаются их механические и антикоррозионные свойства.
Обезуглероживание может происходить и в атмосфере водорода:
4. Электрохимическая коррозия: причины и механизм возникновения
коррозия физический гравитационный модель
На практике чаще всего приходится иметь дело с электрохимической коррозией. Она, в отличие от химической, сопровождается возникновением электрического тока и протекает, как правило, в средах с хорошей ионной проводимостью.
По условиям осуществления различают:
— коррозию в электролитах;
— коррозию под напряжением и др.
Причинами возникновения электрохимической коррозии служат различные виды неоднородностей как самой поверхности металла или сплава, так и коррозионной среды. В результате вся поверхность, соприкасающаяся с токопроводящей коррозионной средой, разделяется на катодные и анодные участки, которые имеют очень малые размеры и чередуются друг с другом. В такой среде они представляют собой совокупность огромного числа короткозамкнутых коррозионных гальванических элементов, вследствие чего электрохимическую коррозию часто называют гальванической коррозией.
В СИСТЕМАХ ВОЗМОЖНО ВОЗНИКНОВЕНИЕ КОРРОЗИОННЫХ НЕ ТОЛЬКО МИКРО-, НО И МАКРОЭЛЕМЕНТОВ, НАПРИМЕР, ПРИ КОНТАКТЕ С ЭЛЕКТРОЛИТОМ ДВУХ СОПРИКАСАЮЩИХСЯ ДЕТАЛЕЙ, ИЗГОТОВЛЕННЫХ ИЗ МЕТАЛЛОВ РАЗЛИЧНОЙ АКТИВНОСТИ (ТАК НАЗЫВАЕТАЯКОНТАКТНАЯ КОРРОЗИЯ).
Процесс электрохимической коррозии представляет собой совокупность двух взаимосвязанных полуреакций., одновременно протекающих на поверхности металла:
а) анодной, сопровождающейся окислением атомов металла на анодных участках поверхности:
б) катодной, сопровождающейся восстановлением окислителя (окисленной формы компонента Оф) коррозионной среды (электролита) на катодных участках поверхности:
1) в аэрированных (насыщенных кислородом) коррозионных средах:
в кислотных (рН + + 4е? 2Н2О (? 0 = 1,229 В);
2) в деарированных (несодержащих растворенный кислород) коррозионных средах:
в кислотных (рН + + 2е? Н2 (? 0 = 0 В);
Коррозию, сопровождающуюся восстановлением молекул кислорода (в аэрированных средах) называют коррозией с поглощением кислорода или коррозией с кислородной деполяризацией.
Рассмотрим наиболее характерные и часто встречающиеся на практике случаи электрохимической коррозии.
Коррозионное разрушение сплава обусловлено его неоднородностью по химическому составу
Скорость этой разновидности электрохимической коррозии в целом тем больше, чем дальше отстоят друг от друга в ряду напряжений металлы, из которых изготовлены детали, образующие макрогальваноэлемент.
— Коррозия под действием блуждающих токов (электрокоррозия). Блуждающими называют токи, ответвляющиеся от своего основного пути. Это токи утечки из электрических цепей или любые токи, попадающие в землю от внешних источников (пути электропоездов, заземления линий тока, электрические кабели и т.п.).
Блуждающие токи вызывают коррозию газо- и нефтепроводов, электрокабелей, различных металлических подземных сооружений. Радиус их действия исчисляется десятками километров. Обычно коррозионные разрушения бывают локального типа и располагаются в местах выхода токов в землю или воду. Для подземных трубопроводов и путей электропоездов это, как правило, места изолированных сочленений и плохого контакта рельсов на стыках соответственно, а также места с недостаточной изоляцией от земли. Они являются анодными зонами и подвергаются усиленной коррозии.
Рассмотренные случаи не исчерпывают всего многообразия электрохимических коррозионных процессов, но дают представления об основных видах неоднородностей, характере взаимодействия изделий с коррозионной средой и причинах возникновения потенциалов в коррозионных средах
Изменение концентрации растворенного вещества в поверхностном слое раствора (или на границе раздела фаз) называют адсорбцией. Если вещество поглощается всем объемом растворителя, то такой процесс называют абсорбцией.
Поверхностные явления определяют такие процессы, как пропитку, экстракцию, флотацию, смазку и др.
Физические процессы и их характеристики
Классификация физических процессов
Все наблюдаемые процессы, характеризующие физические явления и изменения состояний объектов, можно классифицировать в самом общем виде как детерминированные и недетерминированные. К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями. Рассмотрим, например, твердое тело, подвешенное на упругой пружине (рис. 5.1, а).
Пусть m – масса тела, а k – коэффициент жесткости пружины. Предположим, что тело получает начальное смещение Xm из положения равновесия (рис. 5.1, б) и освобождается в момент времени t = 0. На основе фундаментальных законов механики или с помощью повторных наблюдений можно установить справедливость следующего соотношения:
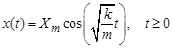
Формула (5.1) достаточно точно описывает положение тела в любой момент времени в недалеком будущем. Для более точного предсказания положения тела в течение длительного времени требуется учесть затухание колебаний. Следовательно, физический процесс, характеризующий движение данного тела, относится к детерминированным.
На практике встречается много физических процессов, которые с высокой точностью могут быть описаны математическими соотношениями. Например, движение спутника по околоземной орбите, изменение напряжения на конденсаторе, который разряжается через сопротивление, вибрация несбалансированного ротора генератора или изменение температуры воды при охлаждении. Детерминированные процессы можно классифицировать, как показано на рис. 5.2.
Рис. 5.1. Тело, подвешенное на пружине
Рис. 5.2. Классификация детерминированных процессов
Существует много процессов, имеющих недетерминированный, т. е. случайный характер. Например, изменение уровня сигнала в канале связи, температура воздуха, мощность, потребляемая из сети в заводском цехе. Точное значение такого процесса в некоторый момент времени в будущем предсказать невозможно. Эти процессы случайны по своей природе и должны описываться не точными уравнениями, а при помощи осредненных статистических характеристик. Будем обозначать случайный процесс x(t) случайной функцией от независимой переменной t.
Случайные процессы можно классифицировать, как показано на рис. 5.3.
Рис. 5.3. Классификация случайных процессов
Во многих случаях трудно решить, относится рассматриваемый физический процесс к детерминированным или случайным. Можно, например, считать, что в действительности ни один физический процесс не является строго детерминированным, поскольку всегда существует возможность того, что в будущем какое-либо непредвиденное событие изменит течение процесса таким образом, что полученные данные будут носить характер иной, чем предполагалось ранее. С другой стороны, можно утверждать, что в действительности ни один физический процесс не имеет строго случайной природы, так как если достаточно хорошо знать механизм изучаемого процесса, его можно описать точными математическими соотношениями.
Практически решение о детерминированном или случайном характере процесса принимается исходя из возможности либо невозможности воспроизведения его при заданных условиях. Если многократное повторение опыта дает одинаковые результаты (с точностью до ошибки измерения), то можно, вообще говоря, считать процесс детерминированным. Если же повторение опыта в идентичных условиях приводит к разным исходам, то природа процесса полагается случайной.
Детерминированные процессы
Детерминированные периодические процессы подразделяются на гармонические и полигармонические. Гармоническими называют процессы, которые могут быть описаны функцией

f0 – циклическая частота, измеряемая в циклах в единицу времени;
q – начальная фаза, рад.
Соотношение (5.2) может быть представлено графически в функции времени и в амплитудно-частотном изображении (спектре), как показано на рис. 5.4.
Циклическая частота 
Полигармонические процессы описываются функцией времени, точно повторяющей свои значения через одинаковые интервалы:

Число циклов в единицу времени называется основной частотой f1.
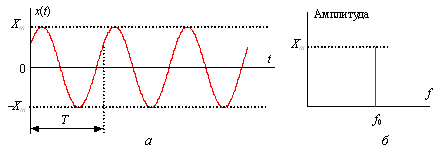
Полигармонический процесс может быть представлен рядом Фурье
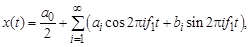
где 
Возможен и другой способ записи ряда Фурье для полигармонического процесса:
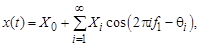
где
Как видно из (5.5), полигармонические процессы состоят из постоянной составляющей X0 и бесконечного числа синусоидальных составляющих, называемых гармониками, с амплитудами Xi и начальными фазами qi. Частоты всех гармоник кратны основной частоте f1.
Полигармонический процесс может имеет вид, показанный на рис. 5.5, а, и соответствующий формуле (5.5) дискретный спектр, показанный на рис. 5.5, б.
Рис. 5.5. Полигармонический процесс и его спектр
В других случаях составляющая с основной частотой может отсутствовать. Предположим, например, что периодический процесс формируется в результате сложения трех синусоидальных функций с частотами 60, 75 и 100 Гц. Наибольший общий делитель этих чисел равен 5 Гц, поэтому период результирующего периодического процесса составляет 0,2 с. Следовательно, при разложении в ряд Фурье значения Xi будут равны нулю при всех i, кроме i = 12, i = 15, i = 20.
Физические процессы полигармонического типа встречаются гораздо чаще простых гармонических процессов. В действительности, когда тот или иной процесс относят к типу гармонических, то зачастую при этом имеют в виду только приближенное представление процесса, который на самом деле является полигармоническим. Например, напряжение на выходе генератора переменного тока содержит небольшие колебания с частотами высших гармоник.
Однако процессы, образованные при суммировании двух или более гармонических функций с произвольными частотами, не будут, вообще говоря, периодическими. Сумма двух или более синусоидальных функций образует периодический процесс только в том случае, если отношение всех возможных пар частот представляет собой рациональные числа. Это означает, что существует некоторый основной период, удовлетворяющий формуле (5.3). Так, процесс
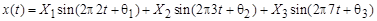
является периодическим, поскольку 2/3, 3/7 и 2/7 – рациональные числа (с основным периодом, равным единице). С другой стороны, процесс
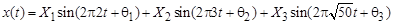
не является периодическим, поскольку числа 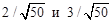
Таким образом, к почти периодическим относятся такие процессы, которые могут быть описаны функцией времени:
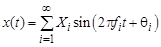
имеющей хотя бы одно отношение fi / fj, которое не является рациональным числом.
Дискретный спектр почти периодического процесса аналогичен спектру полигармонического процесса.
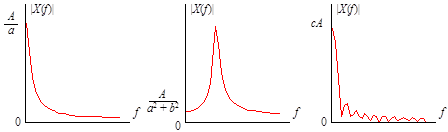
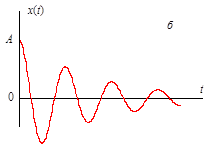
К переходным относятся все непериодические процессы, не являющиеся почти периодическими процессами, описанными выше. Другими словами, переходные процессы включают в себя все не рассмотренные ранее процессы, которые могут быть описаны подходящими функциями времени. Три примера распространенных переходных процессов приведены на рис. 5.6.
 | 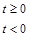 |  |
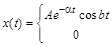 | 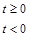 |  б б |
 |  |  в в |
Рис. 5.6. Примеры переходных процессов
Физические переходные процессы весьма многочисленны и разнообразны. Например, процесс, изображенный на рис. 5.6, а, может описывать изменение во времени температуры проводника после отключения протекавшего по нему тока. Кривая на рис. 5.6, б может характеризовать свободные колебания инерционной механической системы после прекращения действия вынуждающей силы. График
Рис. 5.7. Спектры переходных процессов
на рис. 5.6, в может описывать изменение во времени механического напряжения в тросе, который подвешен на опорах линии электропередачи и разрывается в момент c.
Важное отличие переходных процессов от периодических и почти периодических состоит в том, что их невозможно представить с помощью дискретного спектра. Однако в большинстве случаев получают непрерывное спектральное представление переходных процессов, используя интеграл Фурье
Спектр Фурье X(f) в общем случае является комплексной функцией, которая может быть записана в показательной форме:

Здесь 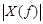
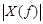
Случайные процессы
Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной. Случайные функции времени называют случайными процессами.
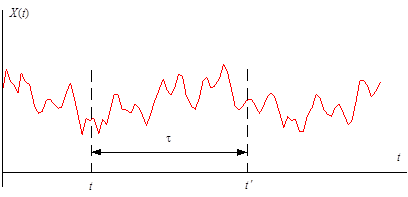
Реализацией случайной функции X(t) (выборочной функцией) называется конкретный вид, который она принимает в результате опыта. Реализация случайного процесса может рассматриваться как элемент множества возможных физических реализаций случайного процесса (рис. 5.8). Совокупность реализаций случайного процесса называется ансамблем реализаций. Совокупность значений реализаций в фиксированный момент времени (выборка случайных значений) называется сечением случайного процесса.
Рис. 5.8. Реализации случайного процесса
В любом сечении случайный процесс есть случайная величина.
Математическое ожидание случайного процесса есть функция времени

Второй центральный момент для двух сечений случайного процесса называется ковариационной функцией
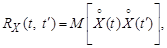
где 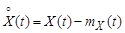
При t = t′ ковариационная функция равна дисперсии случайного процесса
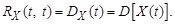
Математическое ожидание и ковариационная функция случайного процесса могут быть найдены по реализациям случайного процесса – осреднением по реализациям:
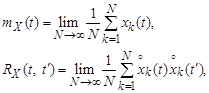
где N – число реализаций случайного процесса.
Если математическое ожидание и ковариационная функция не зависят от времени t, то процесс является стационарным:
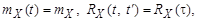
где τ = t′ – t. В (5.14) ковариационная функция зависит только от величины τ, а не от места его расположения на оси времени (рис. 5.9).
Рис. 5.9. Время между двумя сечениями случайного процесса
Возможный вид ковариационной функции показан на рис. 5.10.
Во многих случаях используется нормированная ковариационная (или корреляционная) функция. Для стационарного случайного процесса

Величина корреляционной функции |rX(t)| ≤ 1.
Возможно осреднение по времени отдельных выборочных функций (реализаций). Для k-й выборочной функции имеем:
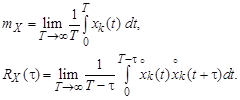
Рис.5.10. Ковариационная функция случайного процесса
Если случайный процесс X(t) стационарен и характеристики mX и RX(τ) одинаковы для различных выборочных функций, то такой процесс называют эргодическим.
Эргодические процессы представляют важный класс случайных процессов.
Нестационарными случайными процессами являются все случайные процессы, не обладающие свойствами стационарности. Эти процессы сложны в исследованиях, и зачастую в задачах по анализу их разбивают на интервалы стационарности или приближенно аппроксимируют стационарными процессами.