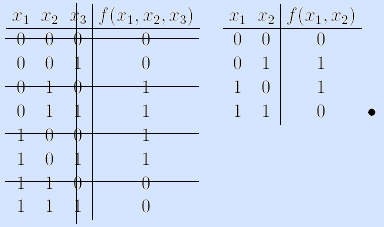что такое фиктивная переменная

Фиктивная переменная

Фиктивная переменая (англ. dummy variable ) — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков принимающих два, но и несколько возможных значения. В этом случае добавляются несколько фиктивных переменных. Фиктивная переменная может быть также индикатором принадлежности наблюдения к некоторой подвыборке. Последнее можно использовать для обнаружения структурных изменений.

Содержание

Моделирование бинарной переменной

Пусть необходимо определить влияние некоторой качественной переменной z, принимающей два возможных значения. Обозначим эти возможные значения A и B для определенности. Тогда такой переменной можно поставить в соответствие следующую фиктивную переменную

Пусть исходная модель имеет вид

Если добавить переменную d в модель, то получим

Тогда при значимом коэффициенте при d получаем две модели для разных значений качественного признака, различающиеся на фиксированный сдвиг (разная константа):

Однако, качественный признак может влиять и на параметры зависимости от факторов x. В этом случае необходимо строить модель:

Таким образом, здесь в модели участвует не только переменная d, но и переменная dx. Это позволяет строить потенциально две разные модели для разных значений качественного признака:

Моделирование многозначного качественного признака

Пусть имеется признак, который принимает несколько возможных значений. Общее правило введения фиктивных переменных следующее: общее количество фиктивных переменных должно быть на единицу меньше количества возможных значений качественного признака, если в модели имеется константа. Это необходимо, чтобы не возникла проблема полной коллинеарности переменных.

Например, уровень образования: нет образования, среднее образование, высшее образование, ученая степень и т. д. В этом случае каждому уровню образования, кроме уровня «нет образования» можно поставить в соответствие некоторую фиктивную переменную.

Фиктивные переменные взаимодействия

Пусть в модели (например, средней заработной платы) участвуют две фиктивные переменные, отвечающие, например, за пол и наличие высшего образования. При обычном включении этих переменных в модель каждая из них дает определенный вклад в изменение коэффициентов модели. Однако, сумма эффектов пола и образования вообще говоря может быть не равна суммарному эффекту этих двух факторов, действующих одновременно. То есть наличие высшего образования у мужчин и у женщин вообще говоря по разному может отражаться на доходе. Поэтому наряду с фиктивными переменными пола и образования можно использовать фиктивную переменную взаимодействия:

Таким образом, данная переменная равна 1, например, для мужчин с высшим образованием и равна нулю для всех остальных случаев (мужчин без высшего образования и женщин независимо от уровня образования).

Источник

Что такое фиктивная переменная

Определение. Говорят, что булева функция f(x₁, …, x_i, …, x_n) существенно зависит от переменной x_i, если выполняется условие

В этом случае также говорят, что переменная x_i существенная, в противном случае ее называют фиктивной переменной.

Пример. Рассмотрим булеву функцию f(x₁, x₂, x₃) и исследуем ее переменные x₁ и x₃.

Из таблиц истинности видно, что переменная x₁ функции f(x₁, x₂, x₃) существенная, так как f(0,x₂, x₃) ≠ f(1,x₂, x₃). Переменная x₃ фиктивная, так как f(x₁, x₂, 0) = f(x₁, x₂, 1). •

Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.

Алгоритм распознавания фиктивной переменной по таблице истинности.

– Для переменной x₁ сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x₁=0, а в нижней x₁=1, если они совпадают, то переменная x₁ фиктивна;

– для переменной x₂ сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x₂ =0, а в нижних x₂ =1, если четвертины в каждой половине совпадают, то переменная x₂ фиктивна;

– и так далее (за четвертинами следуют 1/8, 1/16, … ).

Пример. Для булевой функции из предыдущего примера переменная x₁ существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x₂ существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x₃ фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •

Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.

Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.

Алгоритм удаления фиктивной переменной x_i состоит в вычеркивании из таблицы истинности всех строк, в которых x_i = 0 (или всех строк, в которых x_i = 1), и столбца x_i.

Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x₃ (таблица слева), получаем результат (таблица справа).

Если переменная x_i функции f(x₁, …, x_n) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.

Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).

Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.

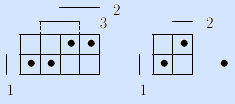
Пример (функция та же и представлена на левой матрице). Переменная x₃ функции фиктивна. Справа показан результат ее удаления.

Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).

Пример. Рассмотрим функции f₁(x₁, x₂) и f₂(x₁, x₂). Удалив фиктивную переменную x₁ функции f₁(x₁, x₂) и фиктивную переменную x₂ функции f₂(x₁, x₂), получим равные функции f₁(x₂)=f₂(x₁)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.

Источник

Как определить фиктивную переменную

Определение. Говорят, что булева функция f(x₁, …, x_i, …, x_n) существенно зависит от переменной x_i, если выполняется условие

В этом случае также говорят, что переменная x_i существенная, в противном случае ее называют фиктивной переменной.

Пример. Рассмотрим булеву функцию f(x₁, x₂, x₃) и исследуем ее переменные x₁ и x₃.

Из таблиц истинности видно, что переменная x₁ функции f(x₁, x₂, x₃) существенная, так как f(0,x₂, x₃) ≠ f(1,x₂, x₃). Переменная x₃ фиктивная, так как f(x₁, x₂, 0) = f(x₁, x₂, 1). •

Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.

Алгоритм распознавания фиктивной переменной по таблице истинности.

– Для переменной x₁ сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x₁=0, а в нижней x₁=1, если они совпадают, то переменная x₁ фиктивна;

– для переменной x₂ сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x₂ =0, а в нижних x₂ =1, если четвертины в каждой половине совпадают, то переменная x₂ фиктивна;

– и так далее (за четвертинами следуют 1/8, 1/16, … ).

Пример. Для булевой функции из предыдущего примера переменная x₁ существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x₂ существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x₃ фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •

Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.

Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.

Алгоритм удаления фиктивной переменной x_i состоит в вычеркивании из таблицы истинности всех строк, в которых x_i = 0 (или всех строк, в которых x_i = 1), и столбца x_i.

Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x₃ (таблица слева), получаем результат (таблица справа).

Если переменная x_i функции f(x₁, …, x_n) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.

Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).

Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.

Пример (функция та же и представлена на левой матрице). Переменная x₃ функции фиктивна. Справа показан результат ее удаления.

Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).

Пример. Рассмотрим функции f₁(x₁, x₂) и f₂(x₁, x₂). Удалив фиктивную переменную x₁ функции f₁(x₁, x₂) и фиктивную переменную x₂ функции f₂(x₁, x₂), получим равные функции f₁(x₂)=f₂(x₁)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.

В вышеприведённых таблицах выделена графа «фиктивные переменные», т.е. переменные, от которых функция на самом деле не зависит. Остановимся на этом понятии подробнее.

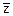
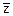
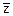
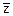
Пример: Рассмотрим булевы функции f(x,y) = xÚy и g(x,y,z) = (xÙy)Ú(хÙ )Ù(yÙz)Ú(yÙ ). Можно заметить, что в силу тождеств алгебры Буля g=(xÚy)Ù(zÚ ), а поскольку zÚ =1, то g = xÚy = f.

В этом примере функция, в которой присутствуют 3 переменных, в действительности зависит от 2-х. В дискретной математике, по сравнению с непрерывной, понятие фиктивных переменных играет большую роль.

Определение: Переменная х является существенной переменной для функции f(x, x₁,…, x_n-1), если существует хотя бы один набор (x₁,…, x_n-1) такой, что f(0, x₁,…, x_n-1) ≠ f(1, x₁,…, x_n-1)

В противном случае переменная называется фиктивной, или несущественной. Понятно, что в определении переменную можно ставить на любое место, и фиктивных переменных может быть несколько.

Ключевым понятием в теории булевых функций является понятие равенства функций. Для функций от одного и того же числа переменных нет необходимости рассматривать какое-то специальное определение равенства, ибо такие функции равны, если они совпадают как отображения одного о того же булева куба. Существование фиктивных переменных усложняет ситуацию, и проблема состоит в том, чтобы определить равенство булевых функций в целом, независимо от числа переменных.

Булевы функции f и g равны, если их существенные переменные совпадают и на каждом наборе значений этих переменных функции f и g принимают равные значения.

Кроме процедуры удаления фиктивных переменных используют и процедуру добавления к множеству переменных булевой функции одной или нескольких переменных.

В результате понятие фиктивной переменной позволяет любые две функции рассматривать как функции от одних и тех же переменных. Для этого надо рассмотреть объединение множеств переменных XUY и дополнить множества X и Y до объединения, вводя соответствующие переменные как фиктивные.

Нетрудно распространить описанную конструкцию на произвольное конечное множество функций и считать тем самым все функции этого множества функциями от одного и того же числа переменных.

Введём понятие проектирующей функции.

Функцию pr_i от n переменных, такую, что

называют (i-ой) проектирующей функцией. В общем случае нумерация множества переменных может быть не задана, и следует указывать не номер, а саму переменную.

Из определения следует, что проектирующая функция имеет единственную существенную переменную, а все остальные переменные проектирующей функции являются фиктивными. Далее мы всегда будем обозначать проектирующую функцию её символом – х, имея в виду возможность расширения на любое число переменных. Такое обозначение есть, конечно вольность, т.к. функция как бы отождествляется с аргументом. Отождествление функции и аргумента недопустимо, т.к. понятие переменной, хоть и связано с понятием функции, никак не есть частный случай понятия функции. Переменная – это имя, некий символ, но никак не функция. Тем не менее мы будем использовать это обозначение ради краткости.

Не нашли то, что искали? Воспользуйтесь поиском:

Вход в систему

Навигация

Последние комментарии

О существенных и фиктивных переменных булевых функций

Воспроизведём данное на лекции определение существенности переменной БФ.

Определение. Пусть задана некоторая БФ f(x₁, x₂, …,x_k, …,x_n).

Переменная x_k этой функции называется существенной, если найдётся набор ДВОИЧНЫХ значений такой, что:

Рассмотрим пример. Пусть БФ f( x₁, x₂, x₃) задана таблицей:

f( x₁, x₂, x₃)

Исследуем переменные этой функции на существенность.

Если в таблично заданной функции f( x₁, x₂, …,x_k, …,x_n), например, переменная x_k – не существенна, то для исключения её из таблицы и, соответственно, уменьшения арности указанной функции, необходимо:

Так как x₂ в выше приведённом примере – не существенна (фиктивна), то действуя так, как описано выше, её из таблицы можно исключить.

В результате получим таблицу:

f(x₁, x₃)

При желании, в полученной таблице, переменные, для удобства, можно переименовать, например, в x₁, x₂, или в x, y. На функцию, как на отображение, такие переименования никакого влияния не окажут.

Ясно, что выполняя описанные операции в обратном порядке, фиктивные переменные можно в таблицу включать, формально увеличивая, тем самым, арность задаваемой этой таблицей БФ.

В дальнейшем, БФ рассматриваются с точностью до их равенства (т.е. равные функции нами различаться не будут).

Если функции f₁ и f₂ равны, то этот факт будем обозначать как f₁ = f₂.

Замечание. Возможность добавления фиктивных переменных позволяет считать что БФ, образующие любое рассматриваемое конечное множество всегда имеют одну и ту же арность.

Критерий фиктивности переменной БФ.

Пусть БФ f(x₁, x₂, …,x_k, …,x_n) определена таблично. Для выявления фиктивности её переменной x_k, удобно использовать следующий критерий:

Задание. Убедитесь в том, что приведённый критерий работает, применив его к переменным x₁, x₂, x₃ рассмотренного выше примера табличного задания БФ f( x₁, x₂, x₃).

Источник

Фиктивные переменные и особенности их использования в моделях

Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику.

В регрессионных моделях с временными рядами используется три основных вида фиктивных переменных:

1) Переменные-индикаторы принадлежности наблюдения к определенному периоду — для моделирования скачкообразных структурных сдвигов.

2) Сезонные переменные — для моделирования сезонности.

3) Линейный временной тренд — для моделирования постепенных плавных структурных сдвигов.

Использование фиктивных переменных имеет следующие преимущества:

В “фиктивной” форме может быть выражена и зависимая переменная. Такая ситуация имеет место, например, при проведении социологических опросов, когда их результат может быть представлен двумя ответами “да”, “нет” (1 или 0) (предполагаемая покупка автомобиля, дачи; желание иметь ребенка в семье и т. п.), а влияющие на этот результат факторы выражаются в произвольной форме (количественные характеристики – уровень дохода, жилая площадь и т. п., качественные характеристики – уровень образования и т. д.).
С формальной точки зрения фиктивные переменные ничем не отличаются от других факторов. Наиболее сложный вопрос, возникающий при их использовании, – это правильная интерпретация получаемых оценок.
Как правило, независимые переменные в регрессионных моделях имеют «непрерывные» области изменения (национальный доход, уровень безработицы, размер зарплаты и т.п.). Однако теория не накладывает никаких ограничений на характер факторов, в частности, некоторые переменные могут принимать всего два значения или, в более общей ситуации, дискретное множество значений. Необходимость рассматривать такие переменные возникает довольно часто в тех случаях, когда требуется принимать во внимание какой-либо качественный признак.
Таким образом,

· Для исследования влияния качественных признаков в модель можно вводить бинарные (фиктивные) переменные, которые, как правило, принимают значение 1, если данный качественный признак присутствует в наблюдении, и значение 0 при его отсутствии;

· Способ включения фиктивных переменных зависит от априорной информации относительно влияния соответствующих качественных признаков на зависимую переменную и от гипотез, которые проверяются с помощью модели;

· От способа включения фиктивной переменной зависит и интерпретация оценки коэффициента при ней.

32. Применение фиктивных переменных при моделировании сезонных

Регрессионная модель, включающая в качестве фактора (факторов) фиктивную переменную, называется регрессионной моделью с переменной структурой.

Рассмотрим временной ряд Xi j,

где i — это номер сезона (периода времени внутри года, напри мер, месяца или квартала);

(L — число сезонов в году);

j — номер года, j = (m — общее количество лет).

Количество уровней исходного ряда равно L × m = n. Число сезонных фиктивных переменных в регрессионной модели всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L − 1. При моделировании годовых данных регрессионная модель, помимо фактора времени, должна содержать одиннадцать фиктивных компонент (12 − 1).

Каждому из сезонов соответствует определенное сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, принимается за базу сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Если имеются поквартальные данные, то значения фиктивных переменных D1, D2, D3 будут принимать следующие значения для каждого из кварталов

Общий вид регрессионной модели с переменной структурой в данном случае будет иметь вид:

yt =β0 +β1 ×t+δ2 ×D2 +δ3 ×D3 +δ4 ×D4 +εt

Построенная модель регрессии является разновидностью аддитивной модели временного ряда. Базисным уравнением исследуемой регрессионной зависимости будет являться уравнение тренда для первого квартала:

Тогда общий вид модели регрессии с переменной структурой будет иметь вид:

Данная модель регрессии представляет собой одну из разновидностей аддитивной модели временного ряда.

На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала:

Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии:

1) частная модель регрессии для второго квартала:

2) частная модель регрессии для третьего квартала:

3) частная модель регрессии для четвёртого квартала:

Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi.

Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции.

Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей.

Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле:

Для поквартальных данных оценка сезонных отклонений осуществляется по формулам:

1) оценка сезонного отклонения для первого квартала:

2) оценка сезонного отклонения для второго квартала:

3) оценка сезонного отклонения для третьего квартала:

4) оценка сезонного отклонения для четвёртого квартала:

Сумма сезонных отклонений должна равняться нулю.

33. Фиктивные переменные сдвига и наклона. Особенности их

использования в моделях.

За качественными переменными скрывается целый комплекс факторов: изменение длины светового дня, среднемесячной температуры воздуха, изменение климатических условий и т.п. При анализе расходов на продукты питания необходимо иметь в виду различия в образе жизни

городского и сельского населения.

На практике приходится учитывать в моделях факторы, носящие качественный характер, значения которых в наблюдениях не возможно измерить с помощью числовой шкалы.

Моделирование влияния пола специалистов на уровень зарплаты.

Моделирование доходов граждан от типа учебного заведения, в котором он получил образование (государственное, частное, специализированное,…)

Модель инфляции с учетом различных видов регулирования со стороны государства

Возможны два подхода к решению задачи:

— построить несколько моделей отдельно для каждого значения (градации) качественной переменной

— учесть влияние качественного фактора в одной модели

Второй способ представляется более прогрессивным, т.к в этом случае появляется возможность оценить статистическую значимость влияния данного фактора на поведение эндогенной переменной на фоне других факторов, внесенных в спецификацию модели

Для учета влияния качественных факторов привлекают переменные, которые получили название фиктивных.

Переход фиктивной переменной с одной градации на другую вызывает скачкообразное изменение эндогенной переменной. Фиктивные переменные, которые приводят лишь к скачкообразному изменению эндогенной переменной, называются фиктивными переменными сдвига.

Однако на практике переход фиктивной переменной с одной градации на другую часто приводит к изменению зависимости эндогенной переменной от количественных переменных. Использование фиктивных переменных в регрессионных моделях позволяет учесть возможность такого поведения эндогенной переменной. Пусть эндогенная переменная y зависит от количественной переменной x и фиктивной переменной r. При этом есть основания предполагать, что зависимость эндогенной переменной от количественного регрессора зависит от уровня фиктивной переменной.

Введение дополнительного слагаемого в спецификацию модели позволяет учесть возможность одновременного сдвига (изменение свободного коэффициента) и наклона (коэффициента при количественном регрессоре) прямой зависимости переменной y от x.

34. Типичные проблемы, возникающие при оценке параметров моделей

в виде системы одновременных уравнений.

Модели могут быть представлены как в виде одного изолированного уравнения, так и в виде системы одновременных уравнений. С помощью таких моделей удается обеспечить системный подход к описанию поведения сложных экономических объектов.

Метод наименьших квадратов при выполнении условий (предпосылок) теоремы Гаусса-Маркова позволяет вычислить несмещенные и эффективные оценки параметров модели в виде изолированного уравнения множественной линейной регрессии. Мы убедились в эффективности МНК при построении как линейных, так и целого ряда нелинейных моделей.

При идентификации (расчете оценок параметров) моделей в виде систем одновременных уравнений неизбежно сталкиваются с двумя проблемами: проблемой идентификации и проблемой авторегрессии в структурной форме моделей.

Проблема идентификации заключается в том, что (здесь возникает проблема с нормальным определением, а в лекции дан огромный пример вместо него)

Чтобы сделать идентифицированным уравнение модели, необходимо ввести дополнительную предопределенную переменную в уравнение смежное с неидентифицируемым. В качестве таких переменных часто используются лаговые эндогенные переменные.

Эта проблема тесно связана с четвертой предпосылкой теоремы Гаусса-Маркова: отсутствие связи между регрессорами уравнения и случайными возмущениями.

Получение состоятельных оценок параметров уравнения с помощью МНК удается за счет значительного увеличения объема выборки только в случае:

получение состоятельных оценок с помощью МНК не возможно.

Именно эта ситуация оказывается типичной для структурных поведенческих уравнений модели.

Источник