что такое фазовые углы кулачка

Основные параметры кулачкового механизма

Профиль кулачка может быть составлен из дуг двух концентрических окружностей и кривых, осуществляющих переход с одной окружности на другую.

Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным . При вращении кулачка толкатель совершает возвратно поступательное или возвратно вращательное движения с остановом в верхнем и нижнем положении. Таким образом в цикле движения толкателя в общем случае можно выделить четыре фазы: удаления, дальнего стояния (или выстоя), сближения и ближнего стояния. В соответствии с этим, углы поворота кулачка или фазовые углы делятся на:

— угол удаления (подъема)

— угол дальнего (верхнего) выстоя

— угол сближения (спуска)

— угол ближнего (нижнего) выстоя.

Сумма трех углов образует угол, который называется рабочим углом

.

В частных случаях могут отсутствовать углы верхнего и нижнего выстоя, тогда .

Кулачок механизма характеризуется двумя профилями:

— центровым (или теоретическим)

— конструктивным (или рабочим).

Под конструктивным понимается наружный рабочий профиль кулачка.

Теоретическим или центровым называется профиль, который в системе координат кулачка описывает центр ролика (или скругления рабочего профиля толкателя) при движении ролика по конструктивному профилю кулачка.

Фазовым называется угол поворота кулачка.

Профильным углом называется угловая координата текущей рабочей точки теоретического профиля, соответствующая текущему фазовому углу . В общем случае фазовый угол не равен профильному.

Перемещение толкателя и угол поворота кулачка отсчитывают от начала фазы подъема, т.е. от наинизшего положения центра ролика, находящегося на расстоянии от центра вращения кулачка. Это расстояние носит название – начального радиуса или радиуса нулевой начальной шайбы и совпадает с минимальным радиус-вектором центрового профиля кулачка.

Максимальное перемещение выходного звена носит название ход толкателя.

Внеосность толкателя – эксцентриситет 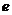— для кулачков с поступательно-движущимся толкателем.

Межосевое расстояние – расстояние между центром вращения кулачка и закрепленной точкой коромысла – для кулачков с коромысловым толкателем.

Угол давления – это угол между скоростью в точке контакта и нормалью к профилю (т.е. направление силы). Обычно этот угол обозначают или . И в одной точке контакта два профиля имеют разный угол давления.

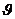
Без учета трения сила направлена по общей нормали в точке контакта профилей. Таким образом, в кулачковом механизме угол давления это угол между нормалью к центровому профилю кулачка и скоростью центра ролика.

Размеры кулачкового механизма определяют из кинематических, динамических и конструктивных условий.

Геометрическая интерпретация аналога скорости толкателя

Кулачек и толкатель образуют ВКП. Толкатель движется поступательно, следовательно, его скорость параллельна направляющей. Кулачек совершает вращательное движение, поэтому его скорость направлена перпендикулярно радиусу вращения в текущей точке и относительная скорость скольжения профилей направлена по общей касательной к ним.

,

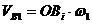
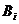
где , а — полюс зацепления в ВКП, который находится на пересечении нормали к профилям в точке контакта с линией центров. Т.к. толкатель движется поступательно, то центр его вращения лежит в бесконечности, и линия центров проходит перпендикулярно скорости через центр кулачка.

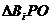
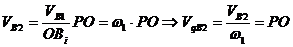
Треугольник скоростей и подобны как треугольники с взаимно перпендикулярными сторонами, т.е. соотношение соответствующих сторон у них постоянно и равно коэффициенту подобия: , откуда .

Т.е. аналог скорости толкателя изображается отрезком перпендикулярным к скорости толкателя, который отсекается прямой параллельной контактной нормали и проходящей через центр кулачка.

Формулировка синтеза: Если на продолжении луча, проведенного из центра ролика 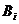перпендикулярно скорости толкателя, отложить от точки отрезок длиной и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена (кулачка) точку .

Таким образом, чтобы получит отрезок , изображающий аналог скорости толкателя надо вектор скорости толкателя повернуть на в сторону вращения кулачка.

Источник

1. R_O – радиус базовой окружности кулачка, это минимальное расстояние от центра вращения кулачка до его центрового профиля.

2. e – эксцентриситет, т.е. смещение оси толкателя от оси, проходящей через центр вращения кулачка. Эксцентриситет величина алгебраическая, т.е. имеющая знак, указывающий на направление смещения с учетом направления вращения кулачка. На рис. 4.1б,в,д,з с учетом того, что кулачок вращается против часовой стрелки, эксцентриситет показан положительным. Если же кулачок вращается по часовой стрелке, то положительным будет смещение в противоположную сторону. У механизмов с плоским толкателем (рис. 4.1д) эксцентриситет является чисто конструктивным параметром.

Механизмы с коромыслом. У механизмов с коромыслом и роликом (рис. 4.1а) основными геометрическими параметрами являются, или пара:

1. R_O – радиус базовой окружности кулачка.

2. L – межцентровое расстояние, от центра вращения кулачка до центра качания коромысла.

1. R_O – радиус базовой окружности кулачка.

Такая неоднозначность объясняется тем, что если одна из величин L или l_к фиксирована, то другая определяется однозначно.

У механизмов с коромыслом и роликом тоже может быть эксцентриситет e, показанный на рис. 4.1а.

У механизмов с плоским коромыслом (рис. 4.1г) основными геометрическими параметрами всегда являются:

1. R_O – радиус базовой окружности кулачка.

2. L – межцентровое расстояние.

4.3. Фазы работы кулачковых механизмов.

Фазовые и конструктивные углы

Кулачковые механизмы могут реализовывать на выходном звене законы движения практически любой сложности. Но любой закон движения может быть представлен комбинацией следующих фаз:

1. Фаза удаления. Процесс перемещения выходного звена (толкателя или коромысла), когда точка контакта кулачка и толкателя удаляется от центра вращения кулачка.

2. Фаза возврата (приближения). Процесс перемещения выходного звена, когда точка контакта кулачка и толкателя приближается к центру вращения кулачка.

3. Фазы выстоя. Ситуация, когда при вращающемся кулачке точка контакта кулачка и толкателя неподвижна. При этом различают, фазу ближнего выстоя – когда точка контакта находится в самом ближнем положении к центру кулачка, фазу дальнего выстоя – когда точка контакта находится в самом дальнем положении от центра кулачка и фазы промежуточных выстоев. Фазы выстоя имеют место, когда точка контакта движется по участку профиля кулачка, имеющего форму дуги окружности, проведенной из центра вращения кулачка.

Приведенная классификация фаз в первую очередь относится к позиционным механизмам.

Каждой фазе работы соответствует свой фазовый угол работы механизма и конструктивный угол кулачка.

Фазовым углом называется угол, на который должен повернуться кулачок, для того, чтобы полностью прошла соответствующая фаза работы. Эти углы обозначаются буквой j с индексом, указывающим тип фазы, например, j_У – фазовый угол удаления, j_Д – фазовый угол дальнего выстоя, j_В – фазовый угол возврата, j_Б – фазовый угол ближнего выстоя.

Конструктивные углы кулачка определяют его профиль. Они обозначаются буквой b с такими же индексами. На рис. 4.2а показаны эти углы. Они ограничены лучами, проведенными из центра вращения кулачка в точки на его центровом профиле, в которых меняется профиль кулачка при переходе от одной фазы к другой.

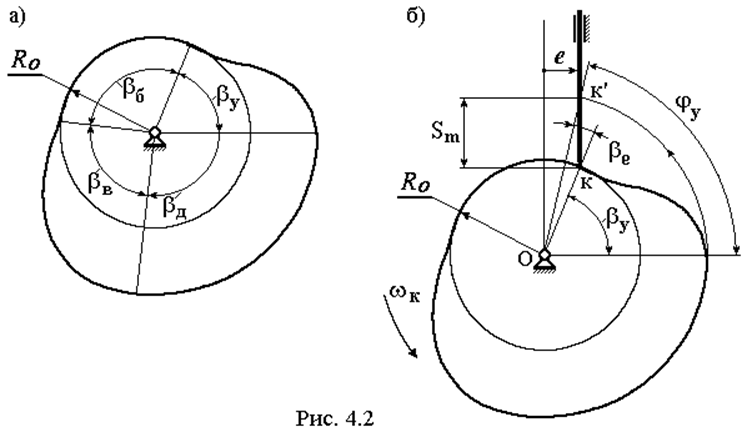На первый взгляд может показаться, что фазовые и конструктивные углы равны. Покажем, что это не всегда так. Для этого выполним построение, показанное на рис. 4.2б. Здесь механизм с толкателем при наличии у него эксцентриситета установлен в положение, соответствующее началу фазы удаления; к – точка контакта кулачка и толкателя. Точка к’ – это положение точки к, соответствующее окончанию фазы удаления. По построению видно, что для того чтобы точка к заняла положение к’ кулачок должен повернуться на угол j_У, не равный b_У, а отличающийся на угол bе, называемый углом эксцентриситета. Для механизмов с толкателем можно записать соотношения:

Источник

Параметры кулачкового механизма

Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2p. В цикле движения толкателя в общем случае можно выделить четыре фазы: удаления, дальнего стояния (или выстоя), сближения и ближнего стояния. В соответствии с этим, углы поворота кулачка или фазовые углы делятся на угол удаления j_y, угол дальнего выстоя j_дв, угол сближения j_с и угол ближнего выстоя j_бв. Сумма углов удаления, дальнего выстоя и сближения образует рабочий угол :

На рис. 4.6 изображена схема плоского кулачкового механизма с двумя видами выходного звена: внеосным с поступательным движением и качающимся (с возвратно-вращательным движением). На этой схеме указаны основные параметры плоских кулачковых механизмов.

Рис. 4.6. Параметры кулачкового механизма

Кулачок механизма характеризуется двумя профилями: центровым (или теоретическим) и конструктивным. Под конструктивным понимается наружный рабочий профиль кулачка. Теоретическим или центровым называется профиль, который в системе координат кулачка описывает центр ролика (или скругления рабочего профиля толкателя) при движении ролика по конструктивному профилю кулачка. Фазовым называется угол поворота кулачка. Профильным углом d_i называется угловая координата текущей рабочей точки теоретического профиля, соответствующая текущему фазовому углу j_i. В общем случае фазовый угол не равен профильному j_i ¹d_i.

Углом давления J называется угол между вектором силы , действующей на ведомое звено с ведущего, и вектором скорости точки приложения этой силы на ведомом звене (рис. 4.7).

Эта сила без учета трения направлена по общей нормали п-п к взаимодействующим поверхностям.

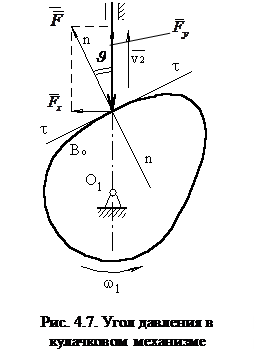
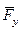
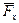
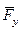
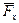
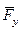
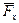
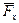
Ее можно разложить на две составляющие: и . Если, в силу каких-либо причин, угол давления будет увеличиваться, то будет уменьшаться, а – увеличиваться. Сила выполняет полезную работу по перемещению толкателя, сила вызывает трение в кинематических парах. С увеличением угла давления растет и сила . При достижении углов больше допустимого, возможен перекос оси толкателя в направляющей.

Угол давления в кулачковом механизме зависит от размеров кулачковой шайбы: чем она больше, тем угол давления меньше.

Для кулачкового механизма с поступательно движущимся толкателем допустимый угол давления равен: [J] = 25º÷35º.

Для кулачкового механизма с качающимся толкателем допустимый угол давления равен: [J] = 35º÷40º.

Источник

Тесты по дисциплине «Теория механизмов и машин» по теме «Кулачковые механизмы»

Тест 1. Кулачком называется:

+ звено, которому принадлежит элемент высшей кинематической пары в форме поверхности переменной кривизны;

— звено, которое движется вращательно;

— звено, которому принадлежит элемент низшей кинематической пары.

Тест 2. Что называется толкателем:

— звено, которое движется возвратно – поступательно;

— звено, которое движется вращательно;

— звено, которому принадлежит элемент низшей кинематической пары;

+ звено, которое воспроизводит заданный закон движения – «жесткую программу».

Тест 3. Какую функцию выполняет ролик в кулачковом механизме:

— осуществляет вращательное движение;

+ уменьшат потери мощности на трение между кулачком и толкателем;

— промежуточное звено между кулачком и толкателем;

— воспроизводит заданный закон движения;

Тест 4. Какое звено в механизме является пассивным:

+ звено, которое не влияет на закон движения толкателя;

— звено, которое не влияет на закон движения кулачка;

— звено, которое воспроизводит заданный закон движения;

— звено, которое воспроизводит закон движения кулачка.

Тест 5. Что такое фазовые углы кулачка:

— угол поворота кулачка, при котором осуществляется подъём толкателя;

— угол поворота кулачка, при котором осуществляется опускание толкателя;

+ углы поворота кулачка, при которых толкатель поднимается, опускается и выстаивает в нижнем и верхнем положении;

— углы выстаивания толкателя в верхнем и нижнем положении.

Тест 6. Чему равна скорость толкателя при фазах его выстаивания:

Тест 7. Что понимается под законом движения толкателя:

— закон перемещения толкателя в функции угла поворота кулачка;

— закон изменения скорости толкателя в функции угла поворота кулачка;

— закон изменения ускорения толкателя в функции угла поворота кулачка;

+ закон изменения перемещения скорости и ускорения толкателя в функции угла поворота кулачка.

Тест 9. Что такое угол движения в кулачковом механизме:

+ угол между вектором линейной скорости толкателя и вектором усилия, передаваемого на толкатель со стороны кулачка;

— угол между векторами линейных скоростей толкателя и кулачка в точке их касания;

— угол между вектором скорости толкателя и вектором угловой скорости кулачка;

— угол между вектором усилия, передаваемого от кулачка на толкатель, и вектором угловой скорости кулачка.

Тест 10. Что такое угол передачи в кулачковом механизме:

+ угол между векторами линейных скоростей толкателя и кулачка в точке их касания;

— угол между векторами линейной скорости толкателя и усилия со стороны кулачка на толкатель;

— угол между вектором скорости толкателя и скорости кулачка;

— угол между нормалью и касательной в точке касания толкателя и кулачка.

Тест 14. Что такое минимальный радиус кулачка и чем он обеспечивается для кулачковых механизмов с роликовым и игольчатым толкателем:

Тест 15. В каком соотношении должны быть угол передачи и минимальный радиус кулачковых механизмов:

— чем меньше, тем больше ;

+ чем больше, тем больше ;

— чем больше ; тем меньше ;

Тест 16. От чего зависит минимальный радиус кулачкового механизма с тарельчатым толкателем:

+ от кривизны профиля кулачка;

— от соотношения угла передачи и угла давления.

Тест 20. Что называется теоретическим профилем кулачка:

— это геометрическое место точек перемещений толкателя;

+ это геометрическое место точек, соответствующее закону перемещения толкателя;

— это кривая перемещения толкателя, соответствующая фазовым углам кулачка;

— это кривая перемещения толкателя.

Тест 21. Что называется практическим профилем кулачка с роликовым толкателем:

— это эквидистантная кривая теоретического профиля;

— это эквидистантная кривая теоретического профиля увеличенная на радиус ролика;

+ это эквидистантная кривая теоретического профиля уменьшенная на радиус ролика;

— это кривая, совпадающая с теоретическим профилем.

Тест 22. Что называется практическим профилем кулачка с игольчатым толкателем:

— это эквидистантная кривая теоретического профиля;

+ это кривая теоретического профиля;

— это кривая перемещения толкателя;

— это геометрическое место точек перемещений толкателя.

Тест 23. Что называется практическим профилем кулачка с тарельчатым толкателем:

+ это огибающая многоугольника, образованного перпендикуляром к радиусам точек теоретического профиля;

— это огибающая многоугольника, образованного касательными к точкам теоретического профиля;

— это огибающая теоретического профиля;

— это эквидистантная кривая теоретического профиля.

Тест 24. Что такое фазовые углы кулачкового механизма:

— это углы подъема, верхнего стояния, опускания и нижнего стояния толкателя

+ это углы поворота кулачка, соответствующие подъёму, опусканию, верхнему и нижнему стоянию толкателя;

— это углы подъёма и опускания толкателя;

— это углы верхнего и нижнего стояния толкателя.

Тест 30. Как влияет смещение толкателя на работу кулачкового механизма с тарельчатым толкателем:

+ способствует повороту толкателя и равномерному износу тарелки;

— увеличивает работосбособность и долговечность;

Источник

Основные геометрические параметры кулачковых механизмов

У механизмов с толкателем основными геометрическими параметрами являются:

1. R_O – радиус базовой окружности кулачка, это минимальное расстояние от центра вращения кулачка до его центрового профиля.

2. e – эксцентриситет, т.е. смещение оси толкателя от оси, проходящей через центр вращения кулачка. Эксцентриситет величина алгебраическая, т.е. имеющая знак, указывающий на направление смещения с учетом направления вращения кулачка. На рис. 3.1бв,д,з с учетом того, что кулачок вращается против часовой стрелки, эксцентриситет показан положительным. Если же кулачок вращается по часовой стрелке, то положительным будет смещение в противоположную сторону. У механизмов с плоским толкателем (рис. 3.1д) эксцентриситет является чисто конструктивным параметром.

Механизмы с коромыслом. У механизмов с коромыслом и роликом (рис. 3.1а) основными геометрическими параметрами являются, или пара:

1. R_O – радиус базовой окружности кулачка.

2. L – межцентровое расстояние, от центра вращения кулачка до центра качания коромысла.

1. R_O – радиус базовой окружности кулачка.

2. l_К – длина коромысла.

Такая неоднозначность объясняется тем, что если одна из величинL или l_к фиксирована, то другая определяется однозначно.

У механизмов с коромыслом и роликом тоже может быть эксцентриситет e, показанный на рис. 3.1а, но для них основным геометрическим параметром он не является.

У механизмов с плоским коромыслом (рис. 3.1г) основными геометрическими параметрами всегда являются:

1. R_O – радиус базовой окружности кулачка.

2. L – межцентровое расстояние.

Фазы работы кулачковых механизмов.

Фазовые и конструктивные углы

Кулачковые механизмы могут реализовывать на выходном звене законы движения практически любой сложности. Но любой закон движения может быть представлен комбинацией следующих фаз:

1. Фаза удаления. Процесс перемещения выходного звена (толкателя или коромысла), когда точка контакта кулачка и толкателя удаляется от центра вращения кулачка.

2. Фаза возврата (приближения). Процесс перемещения выходного звена, когда точка контакта кулачка и толкателя приближается к центру вращения кулачка.

3. Фазы выстоя. Ситуация, когда при вращающемся кулачке точка контакта кулачка и толкателя неподвижна. При этом различают, фазу ближнего выстоя – когда точка контакта находится в самом ближнем положении к центру кулачка, фазу дальнего выстоя – когда точка контакта находится в самом дальнем положении от центра кулачка и фазы промежуточных выстоев. Фазы выстоя имеют место, когда точка контакта движется по участку профиля кулачка, имеющего форму дуги окружности, проведенной из центра вращения кулачка.

Приведенная классификация фаз в первую очередь относится к позиционным механизмам.

Каждой фазе работы соответствует свой фазовый угол работы механизма и конструктивный угол кулачка.

Фазовым углом называется угол, на который должен повернуться кулачок, для того, чтобы полностью прошла соответствующая фаза работы. Эти углы обозначаются буквой j с индексом, указывающим тип фазы, например, j_У – фазовый угол удаления, j_Д – фазовый угол дальнего выстоя, j_В – фазовый угол возврата, j_Б – фазовый угол ближнего выстоя.

Конструктивные углы кулачка определяют его профиль. Они обозначаются буквой b с такими же индексами. На рис. 3.2а показаны эти углы. Они ограничены лучами, проведенными из центра вращения кулачка в точки на его центровом профиле, в которых меняется профиль кулачка при переходе от одной фазы к другой.

На первый взгляд может показаться, что фазовые и конструктивные углы равны. Покажем, что это не всегда так. Для этого выполним построение, показанное на рис. 3.2б. Здесь механизм с толкателем при наличии у него эксцентриситета установлен в положение, соответствующее началу фазы удаления; к – точка контакта кулачка и толкателя. Точка к’ – это положение точки к, соответствующее окончанию фазы удаления. По построению видно, что для того чтобы точка к заняла положение к’ кулачок должен повернуться на угол j_У, не равный b_У, а отличающийся на угол bе, называемый углом эксцентриситета. Для механизмов с толкателем можно записать соотношения:

Дата добавления: 2018-05-12 ; просмотров: 746 ; Мы поможем в написании вашей работы!

Источник