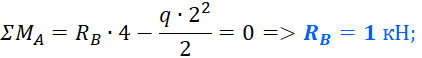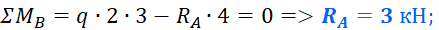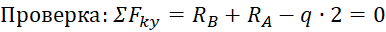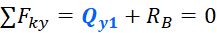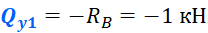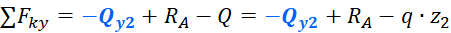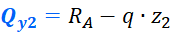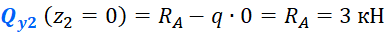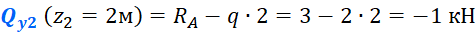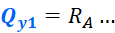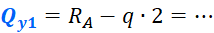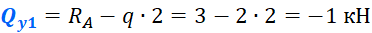Что такое эпюра изгибающих моментов
Построение эпюр при изгибе для балки — экспресс курс для чайников
Привет! Вы находитесь на сайте – sopromats.ru, проекте о сопромате и не только! Это новая статья из серии – «сопромат для чайников», в которой я расскажу о построении эпюр при изгибе для балки. Как обычно, буду писать просто и по делу. Здесь я не буду спамить специфическими фразами из сопромата и рассматривать сложные примеры. Будем учиться на простейшей балке. Ну что же давайте начнем учиться!
Сколько можно нарисовать эпюр при изгибе для балок?
Для простого изгиба, который будем рассматривать в этой статье, можно нарисовать всего две эпюры. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов. Одна показывает распределение внутренних сил внутри элемента, работающего на изгиб, другая моментов. Если хотите, можете изучить больше информации по этим силовым факторам в следующих материалах:
Если Вам лень читать эти статьи, то ничего. Это нормально 🙂 Просто хотел пропиарить немного эти материалы, не зря же я их писал…В этой статье, для чайников, мы, итак, научимся строить эти эпюры, но только одним методом.
Подготовительные работы
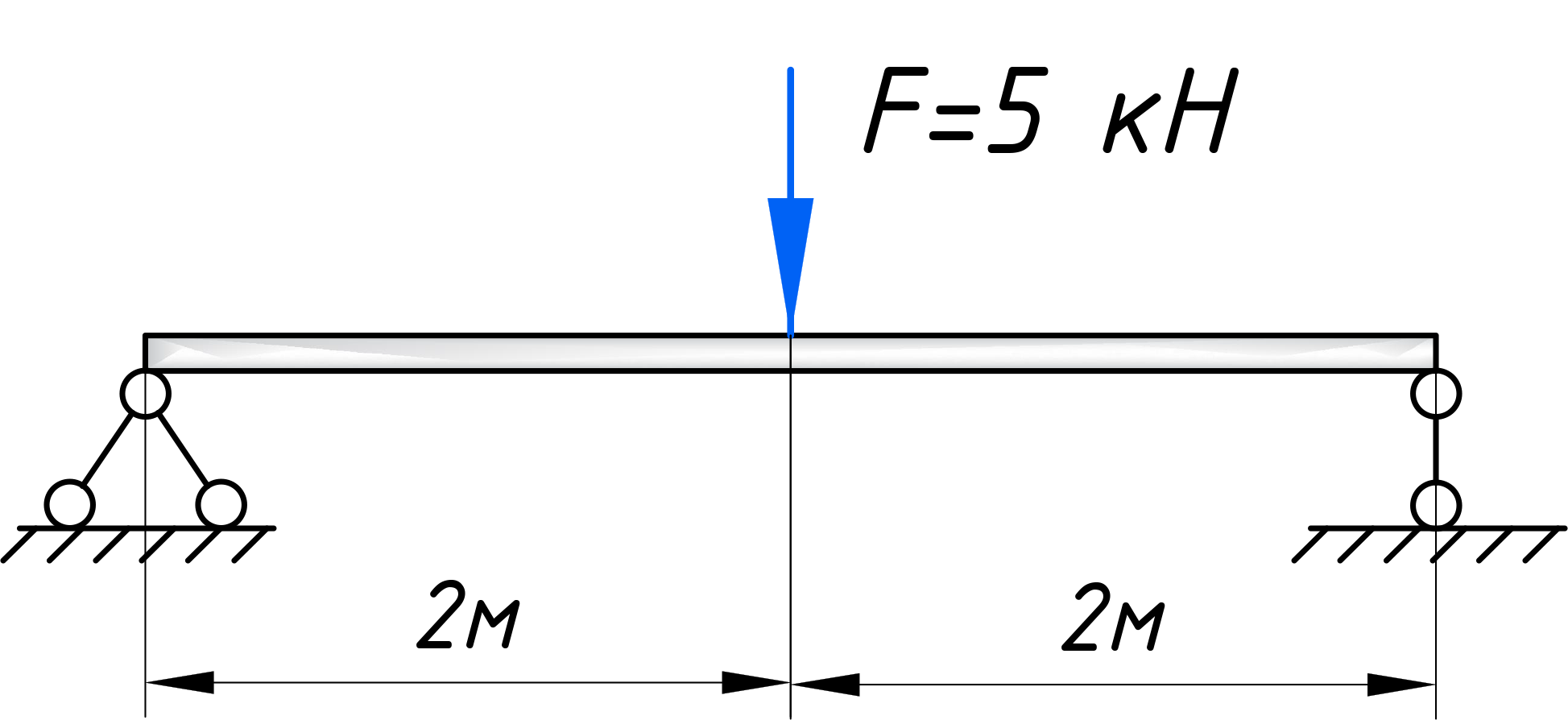
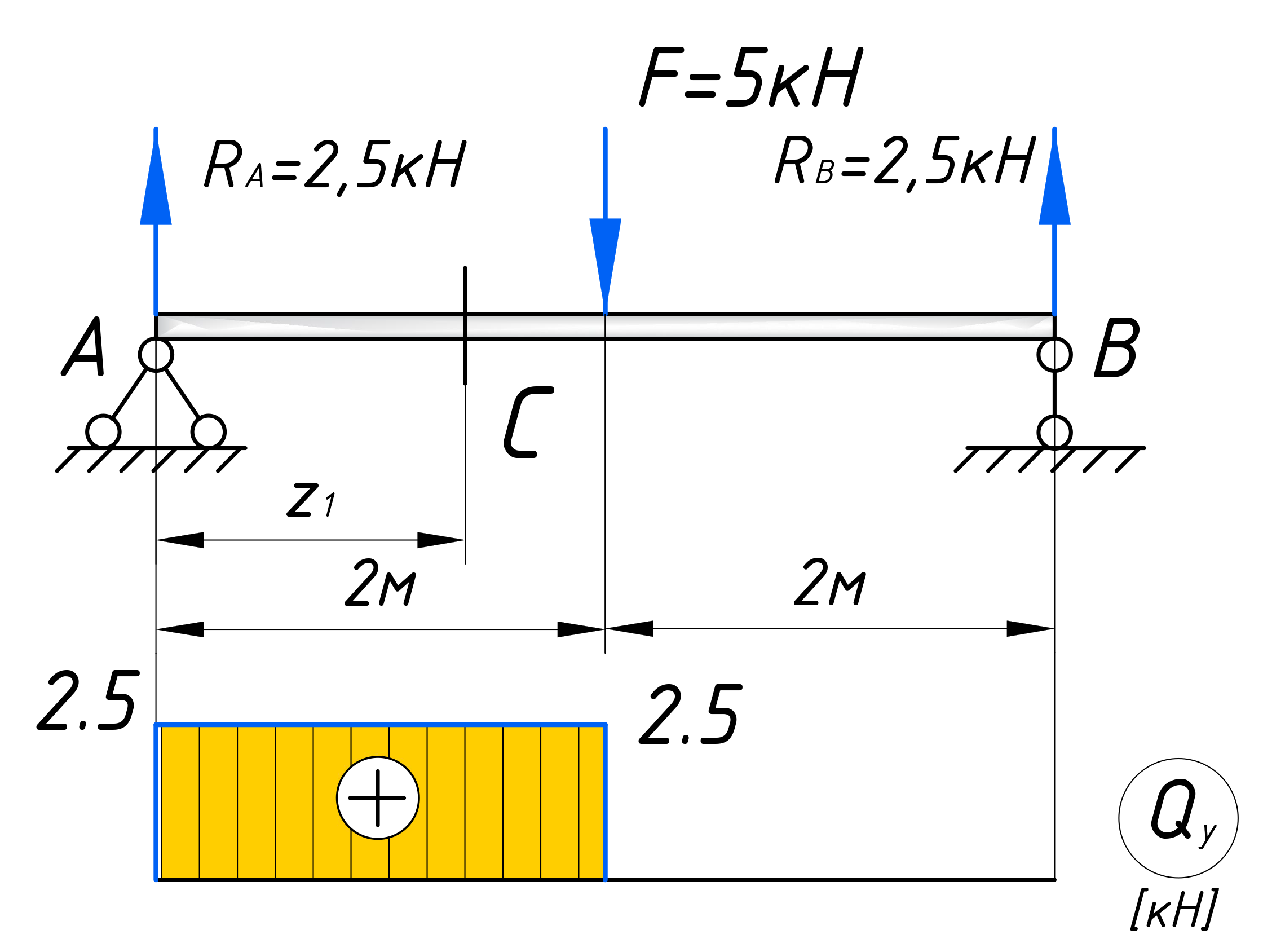
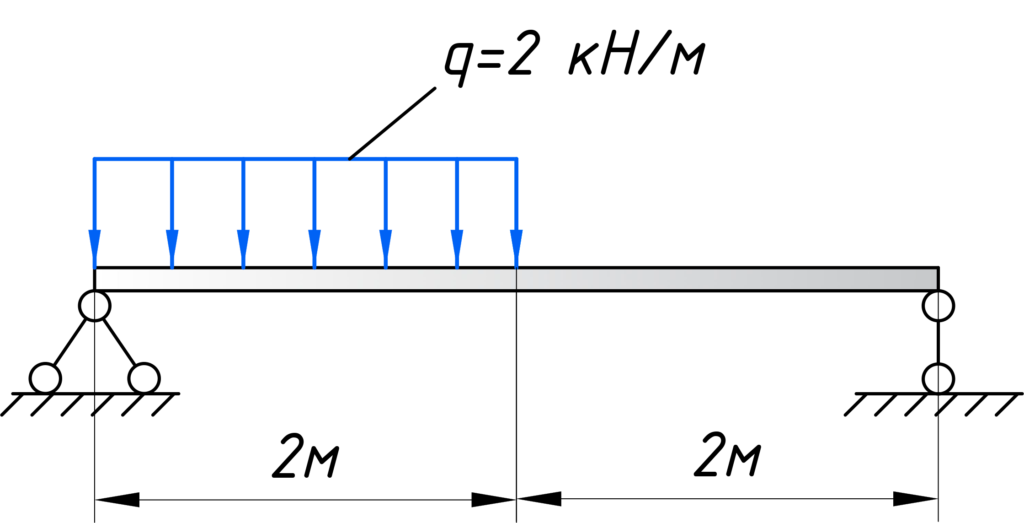
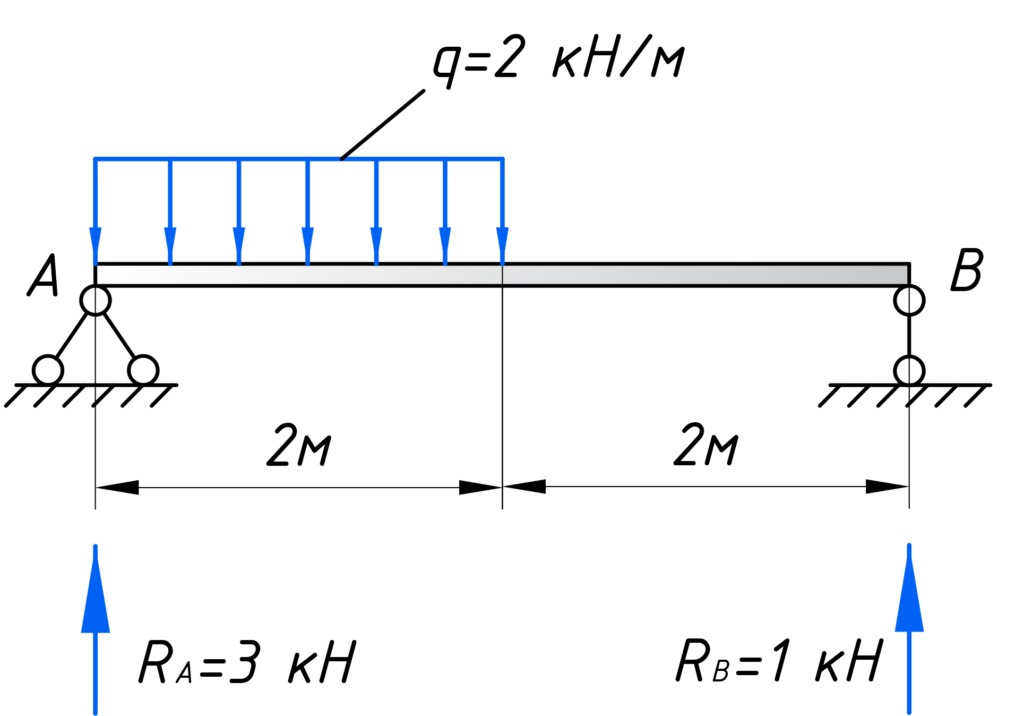
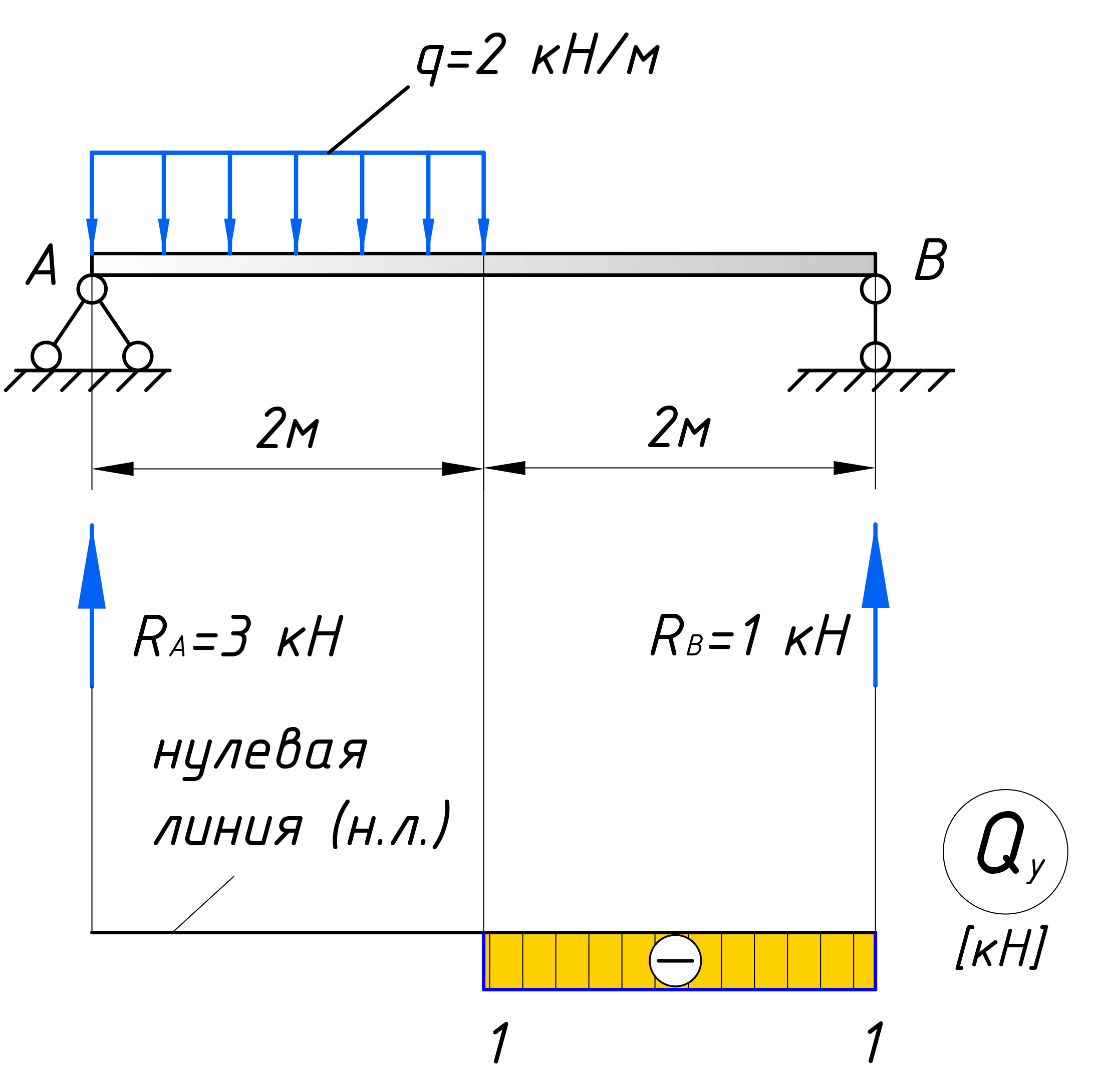
Для того, чтобы построить эпюры, первым делом вычертите расчетную схему, с указанием всех нагрузок и размеров:
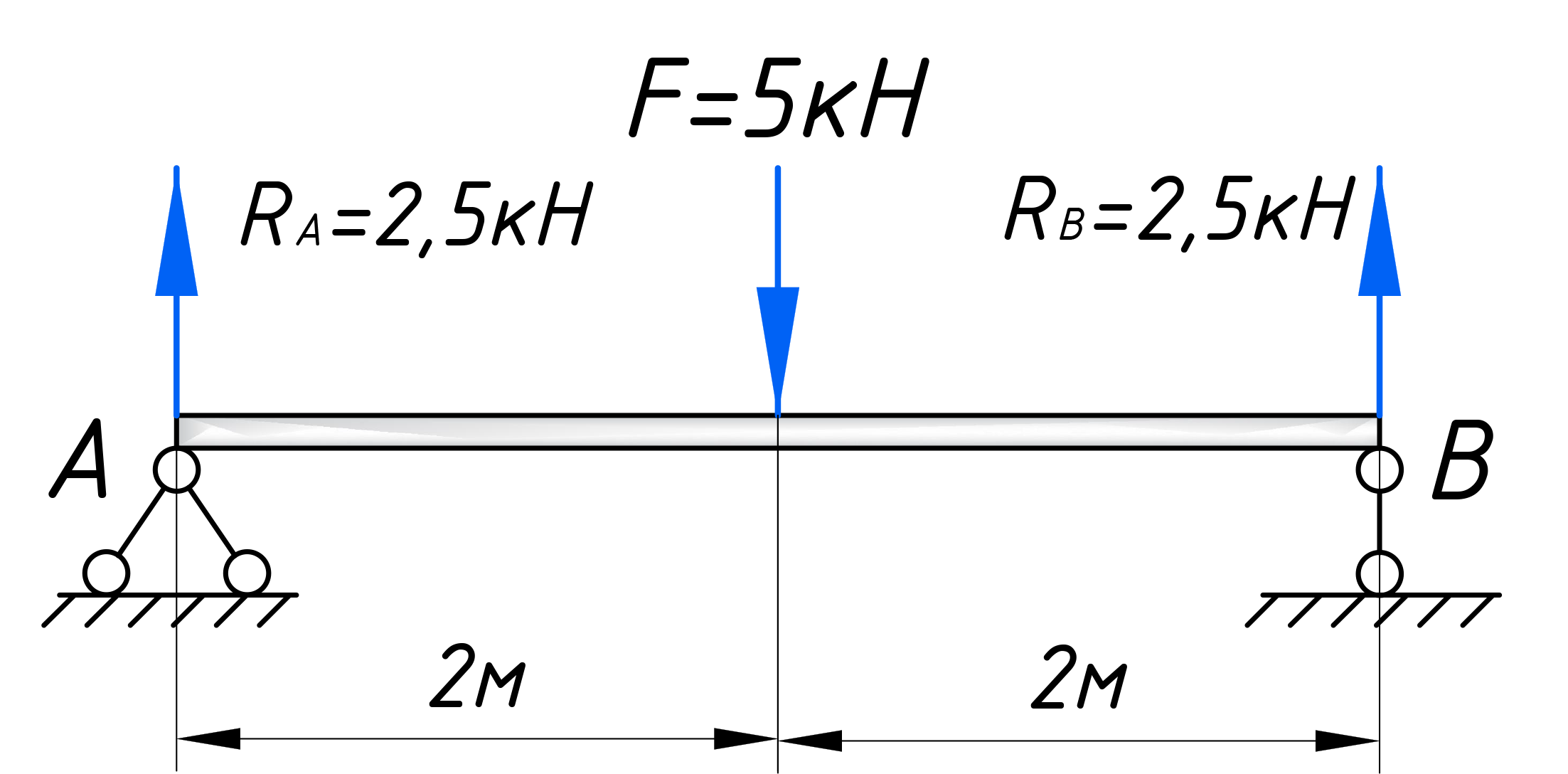
После этого нужно определить реакции опор. Без них дальше никуда. Если Вы не умеет этого делать, обязательно прочтите этот урок про расчет реакций опор для чайников. Здесь же сразу приведу результат вычислений:
Расчет и построение эпюр
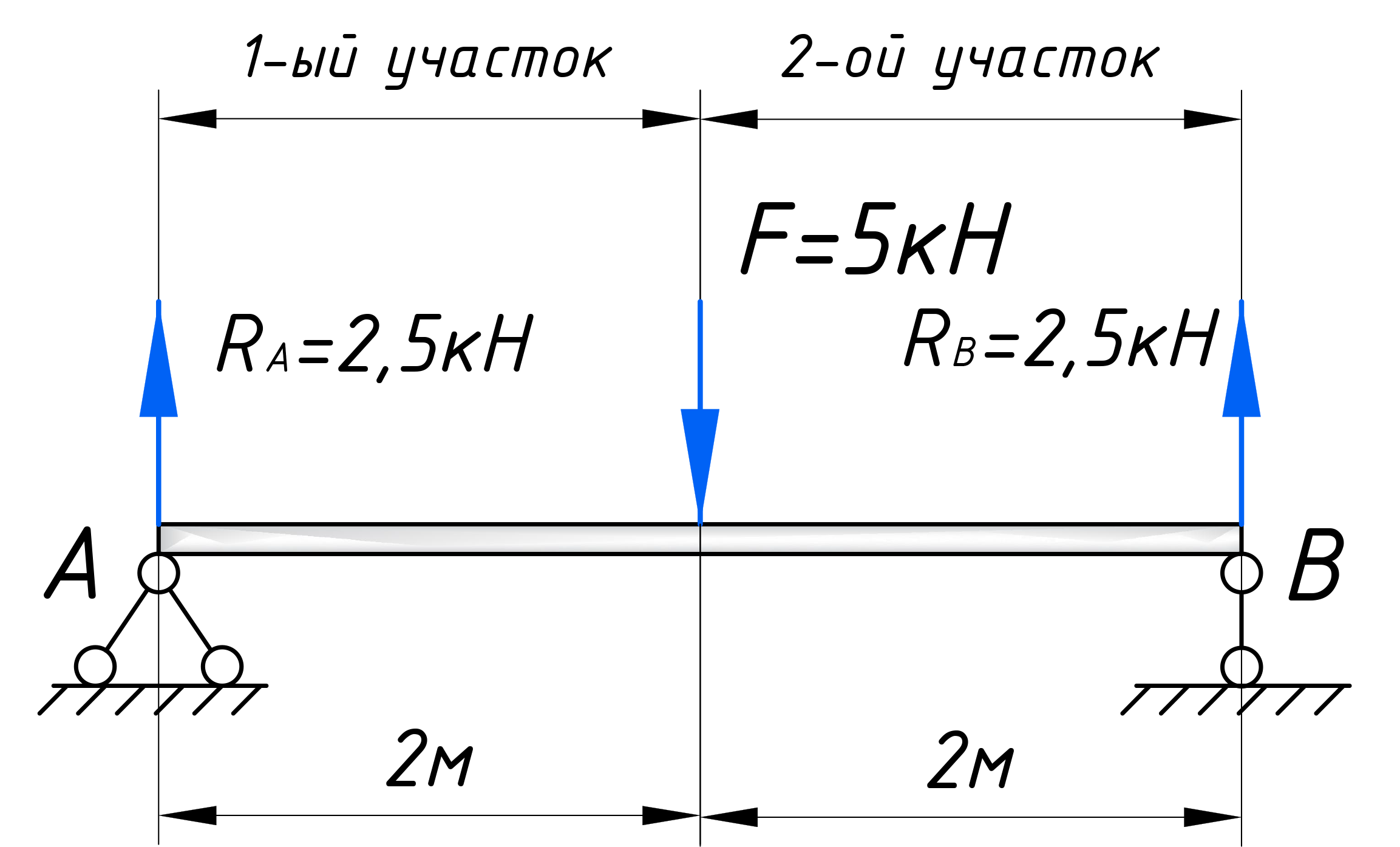
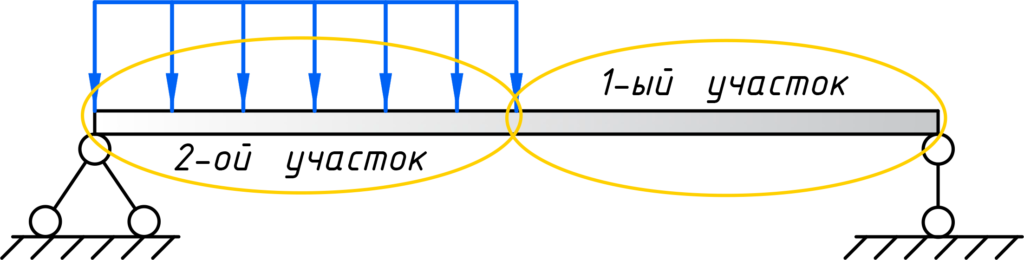
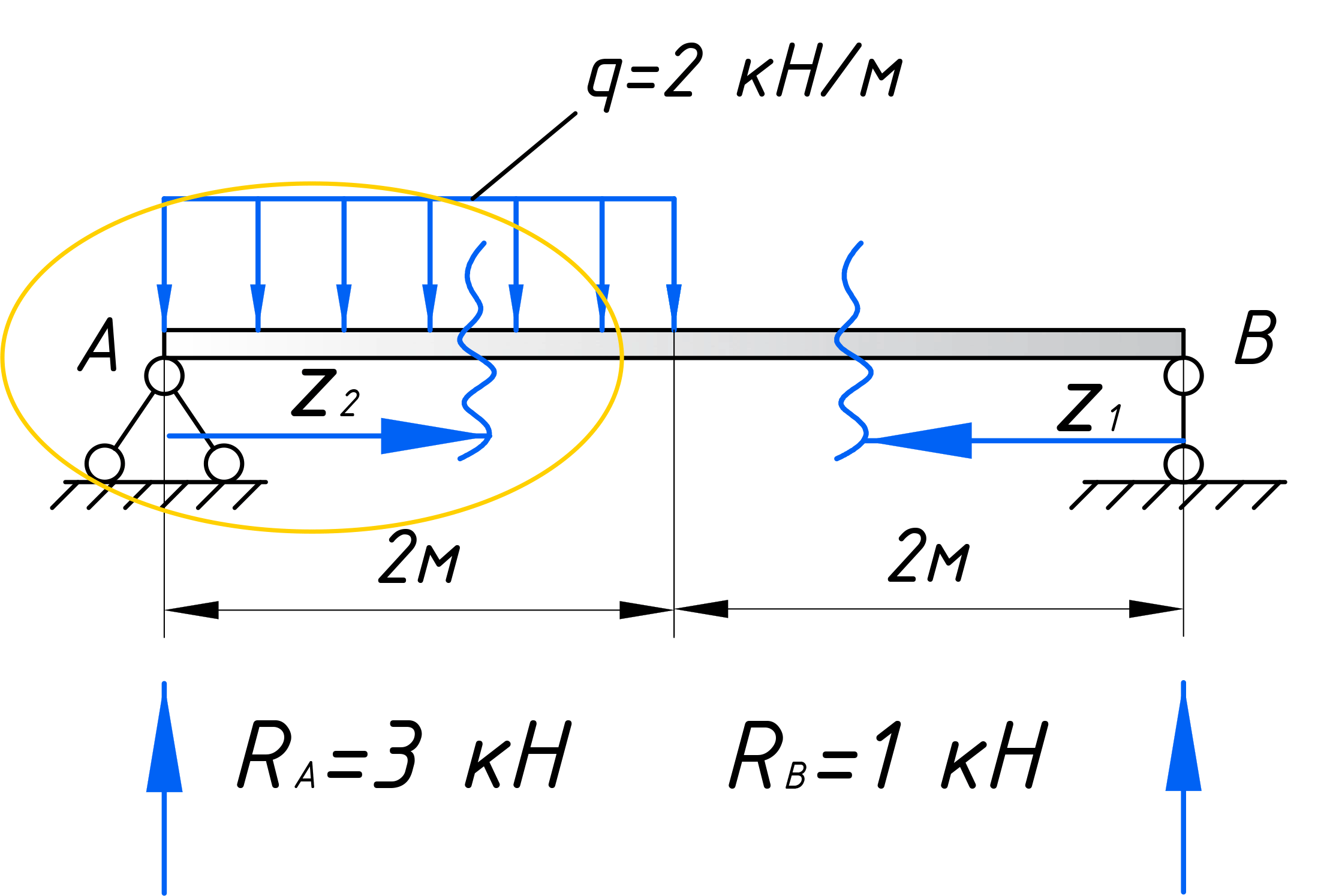
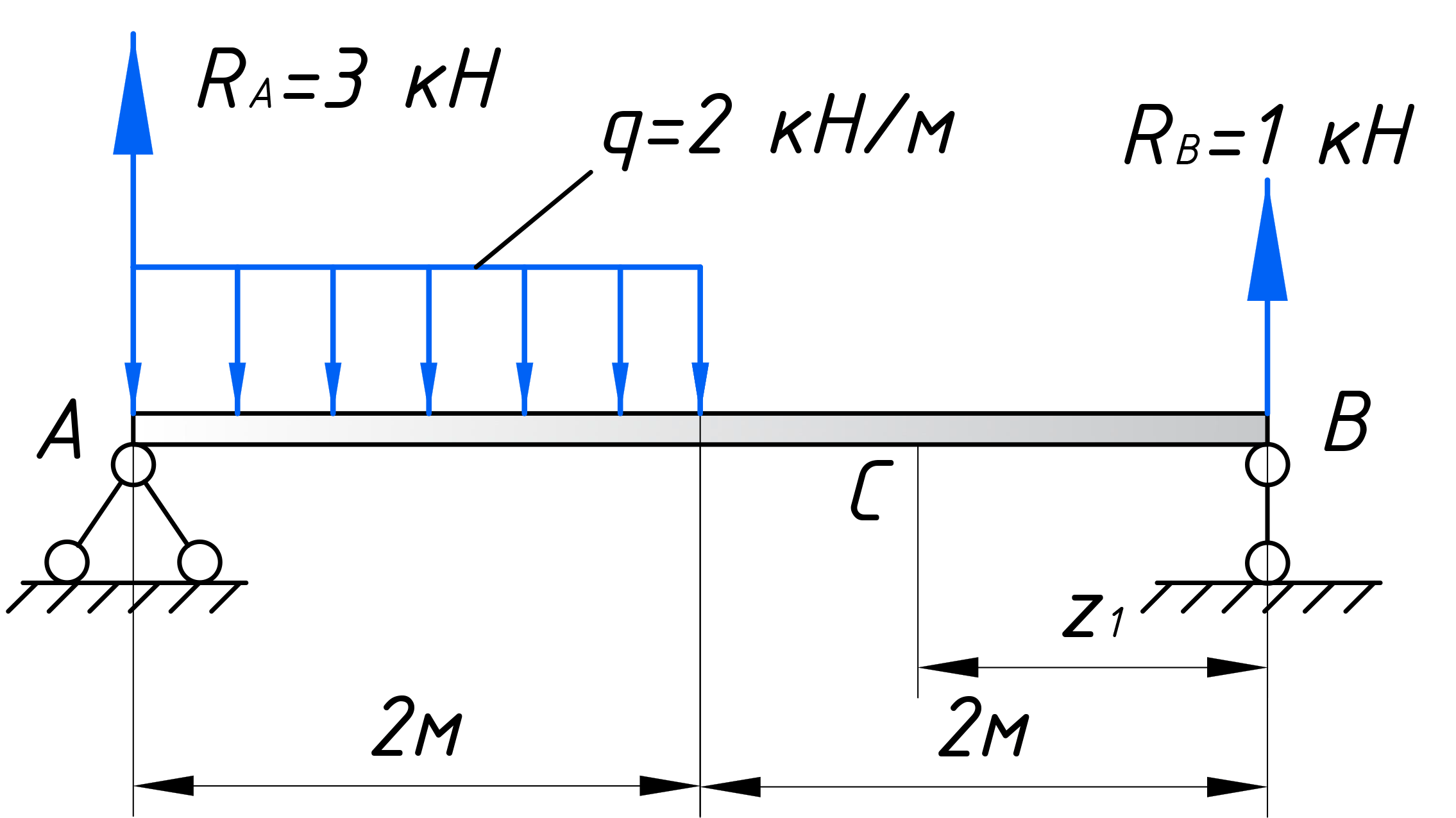
Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:
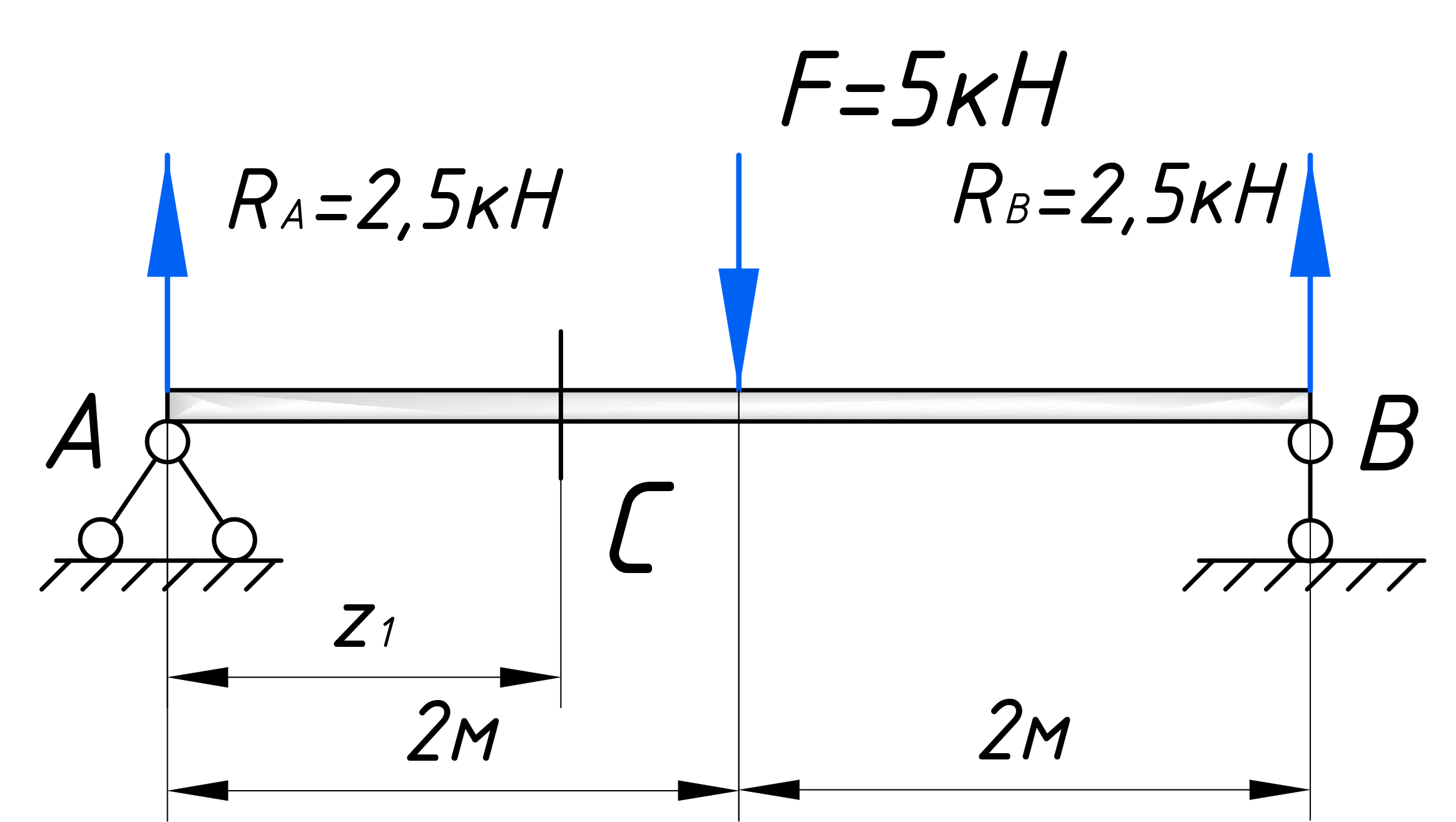
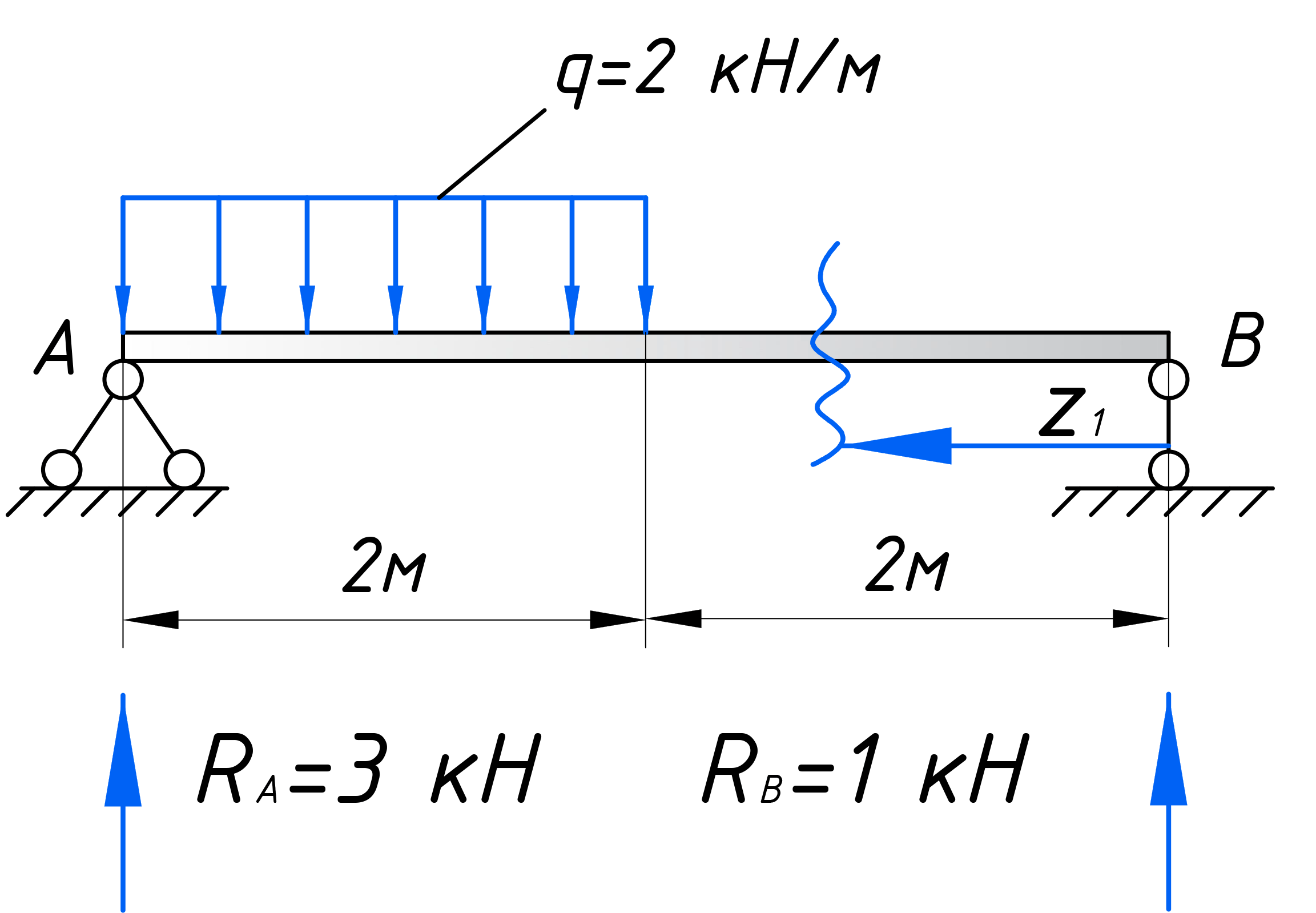
Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:
Записываем уравнение для поперечной силы
Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).
В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:
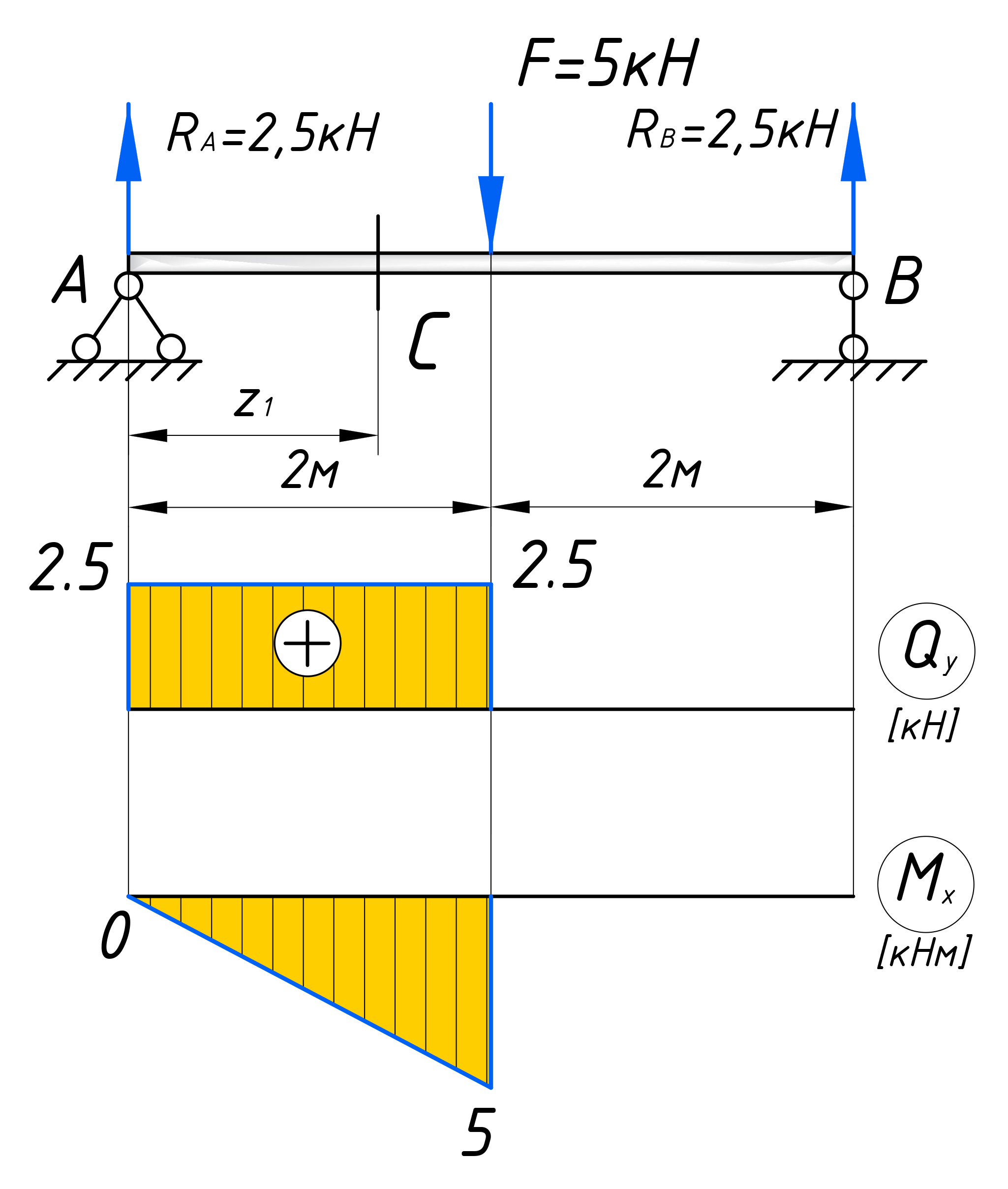
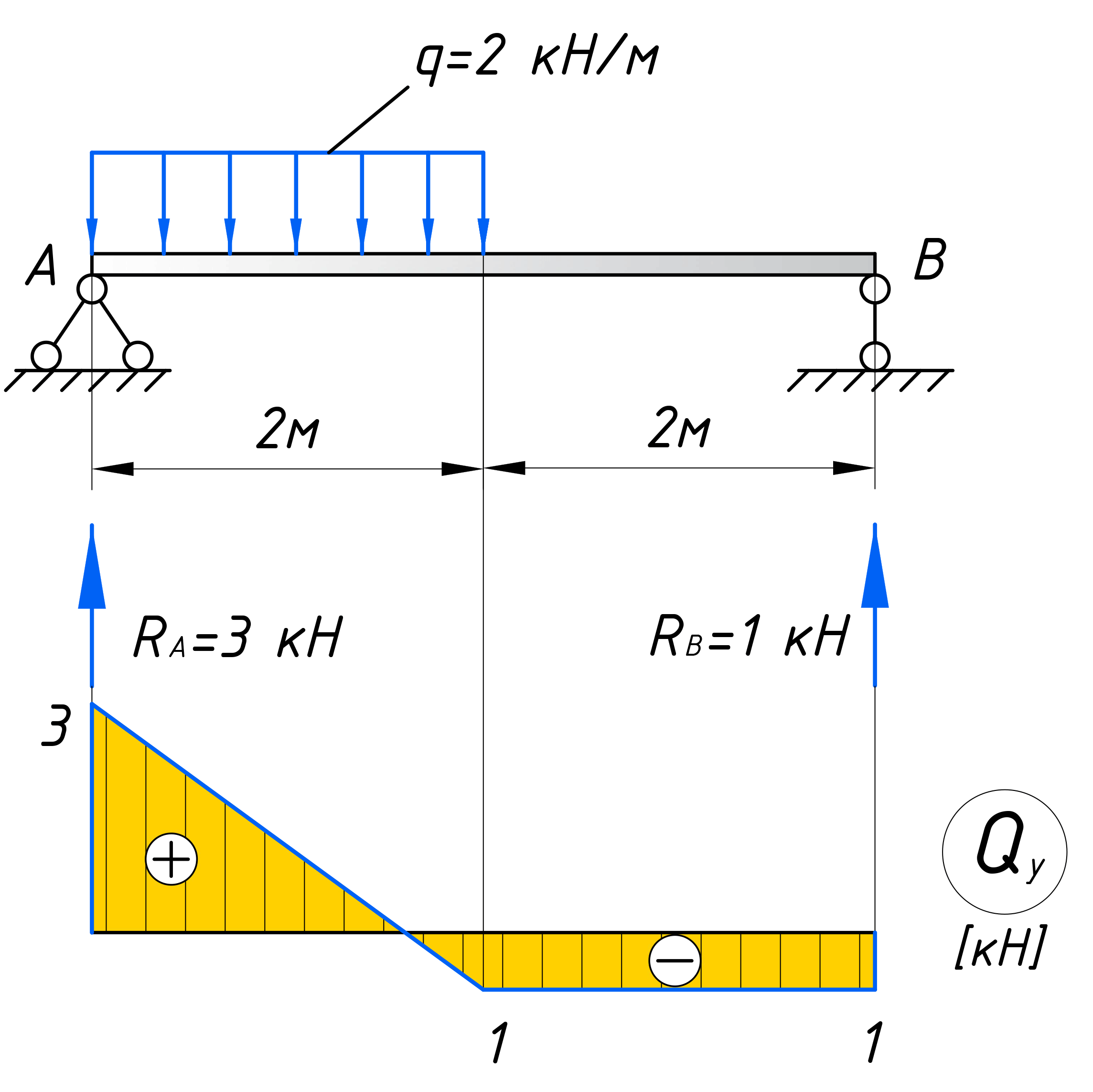
Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:
Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.
Записываем уравнение для изгибающего момента
Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.
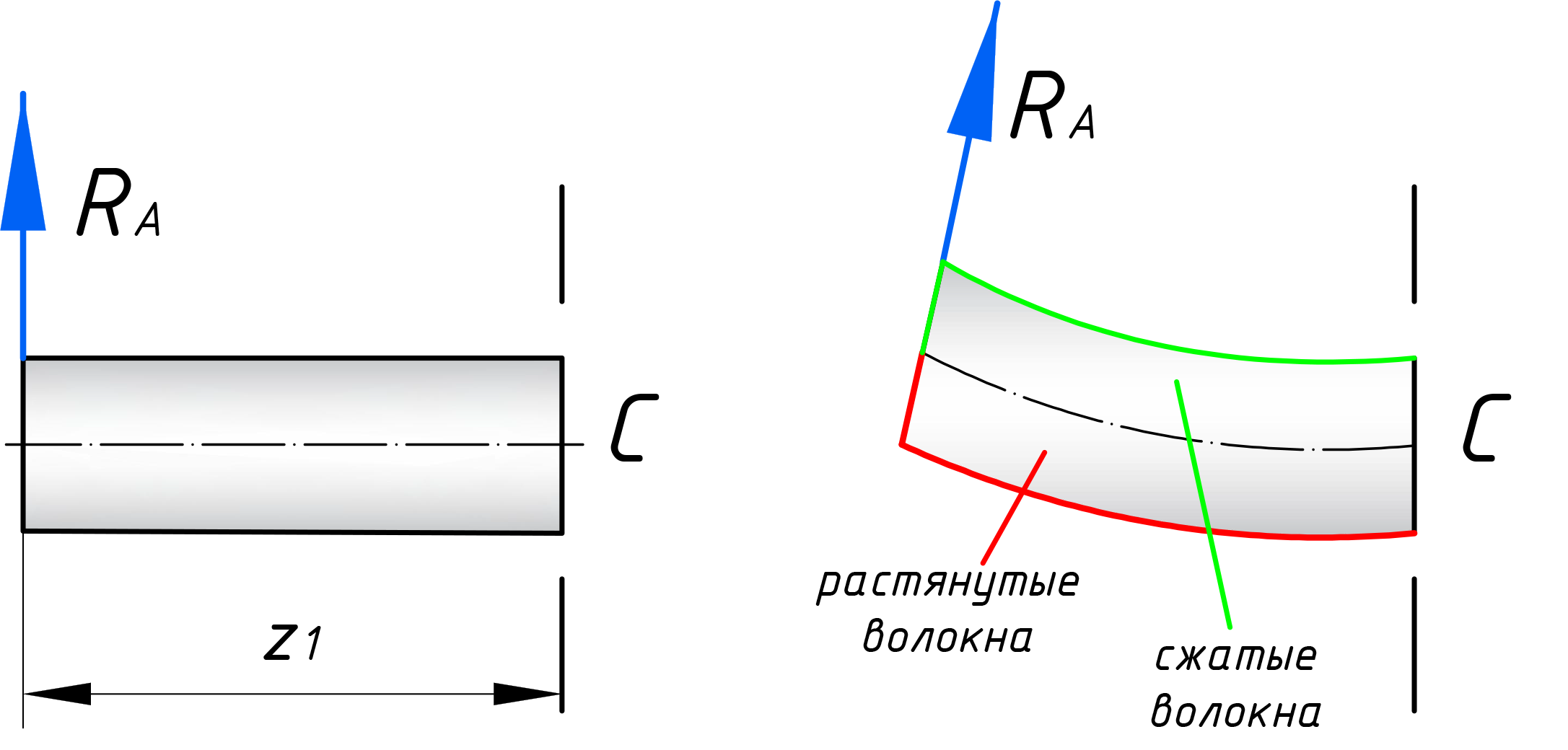
Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:
Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:
Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:
Эпюры для второго участка балки
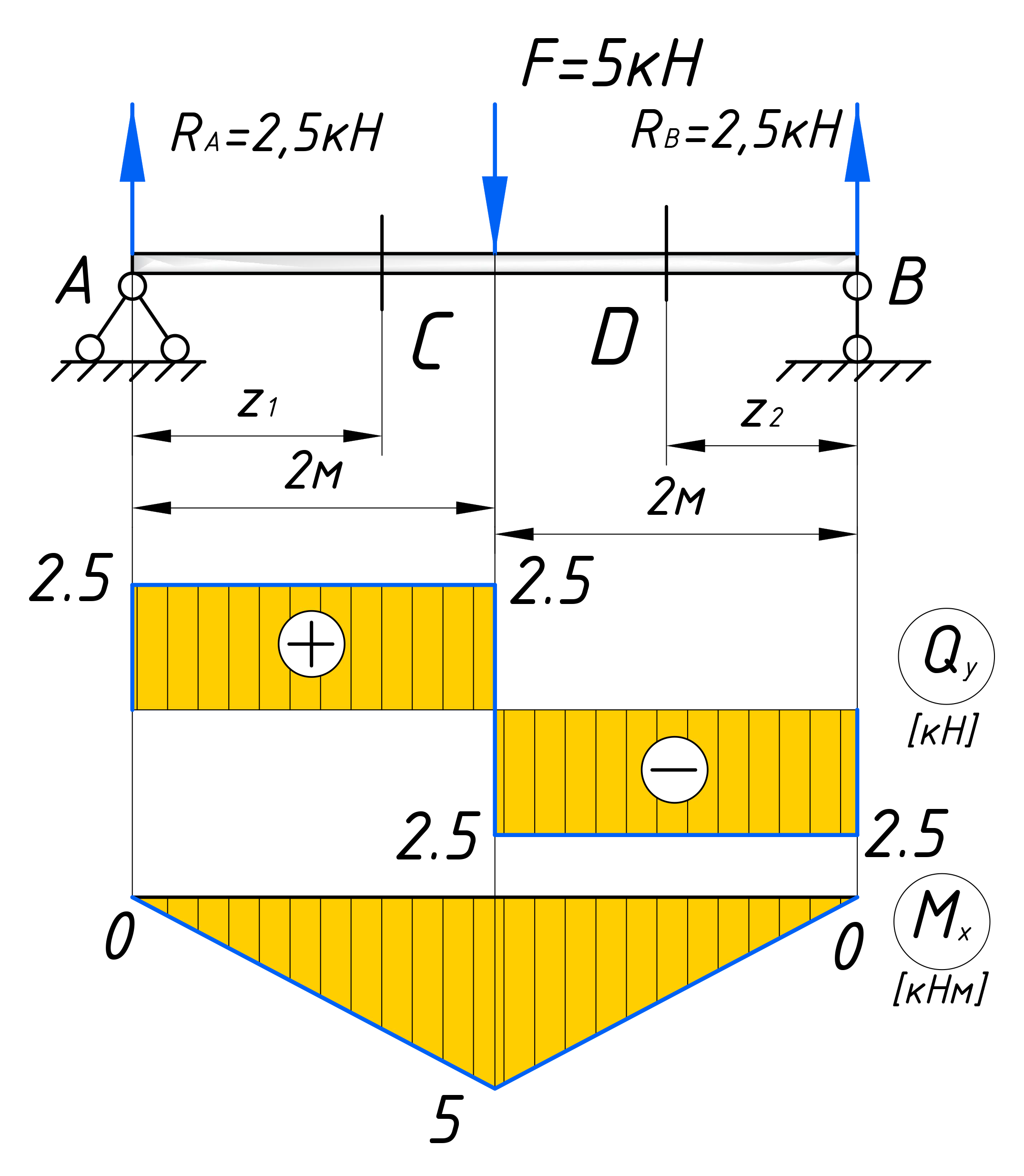
С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:
Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.
Спасибо за внимание! Если Вам понравилась статья, да и сайт в целом, добавляйте его в свои закладки, чтобы иметь быстрый доступ к нему, а также подписывайтесь на наши соц. сети, делитесь этой статьей с друзьями и т.д. Буду благодарен 🙂
Тема 2.5. Изгиб
Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.1). Брус, работающий при изгибе, называется балкой.
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.1).
Рис.1. Прямой изгиб
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.2). При наличии поперечной силы Qy изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Рис.2. Чистый изгиб
Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы:
— Определение внутренних усилий в балках и построение эпюр внутренних усилий.
— Проверка прочности балок.
— Определение перемещений и проверка жесткости балок.
§2.Построение эпюр поперечной силы и изгибающего момента
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.
Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.
Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.
Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.
Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 3 показаны эти закрепления. Для неподвижной (рис 3,б) и подвижной (рис. 3,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.3,в).
Рис.3. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;
в – в шарнирно-подвижной опоре.
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.
Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).
Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.
Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.
Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.
Поперечная сила Q в каком-либо поперечном сечении балки численно равная алгебраической сумме на ось у внешних сил действующих на балку по одну сторону от рассматриваемого сечения, а изгибающий момент M равен алгебраической сумме моментов сил, относительно центра тяжести сечения.
Взаимосвязь между нагрузкой и очертаниями эпюр поперечных сил Q и изгибающих моментов M:
Указанные закономерности позволяют упростить построения эпюр поперечных сил и изгибающих моментов (в сложнoзагруженных балках) и обойтись без составления уравнений для каждого участка.
Для определения максимальных значений изгибающих моментов дополнительно подсчитываются моменты в сечениях, где поперечные силы равны нулю. Построение без составления эпюр уравнений дает особенно значительный эффект для балок, нагруженных сложной нагрузкой, имеющих много участков нагружения.
Эпюра поперечных сил — как построить?
Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!
Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.
Подробный способ построения эпюры поперечных сил
В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:
Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:
Разбиваем балку на участки
После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.
Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.
Метод сечений
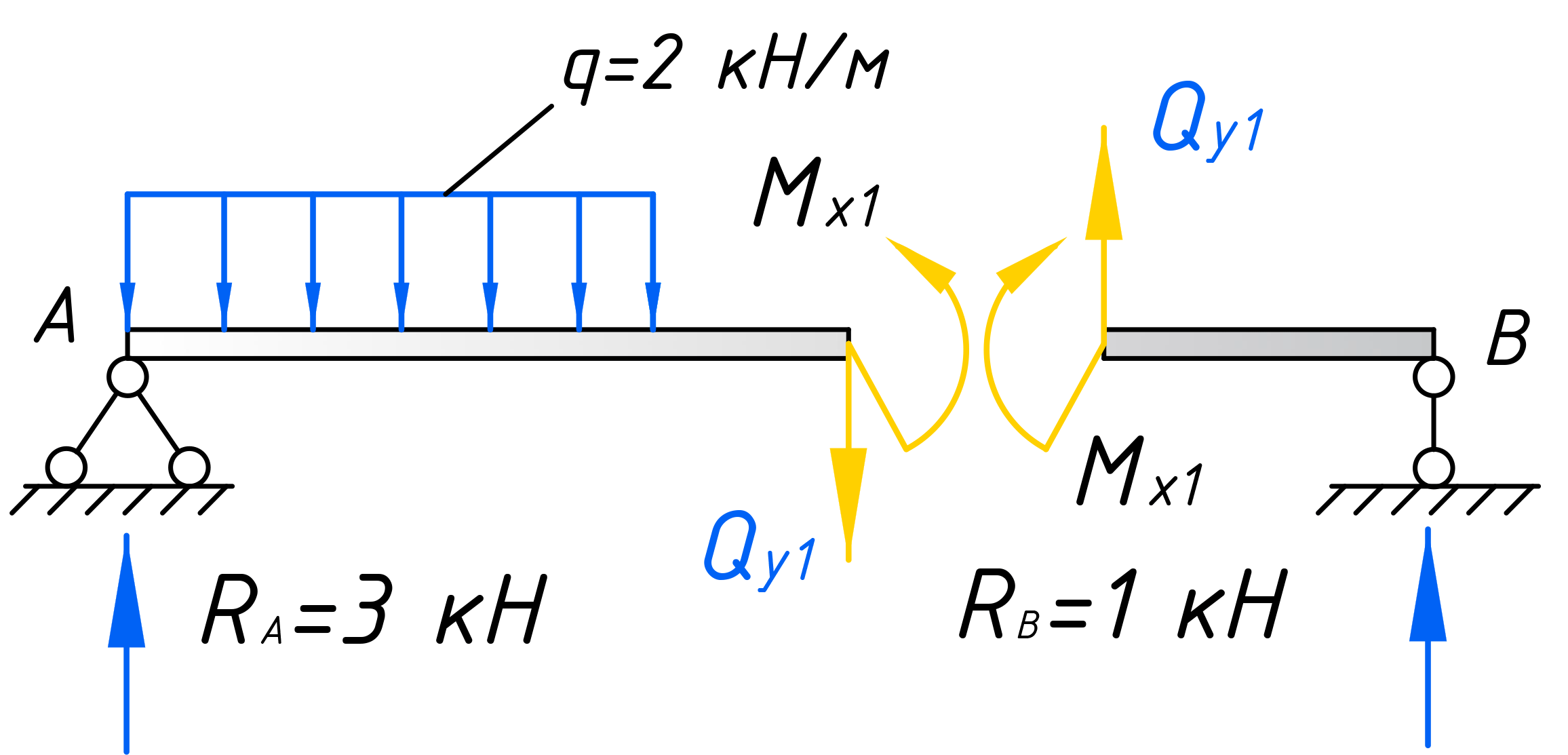
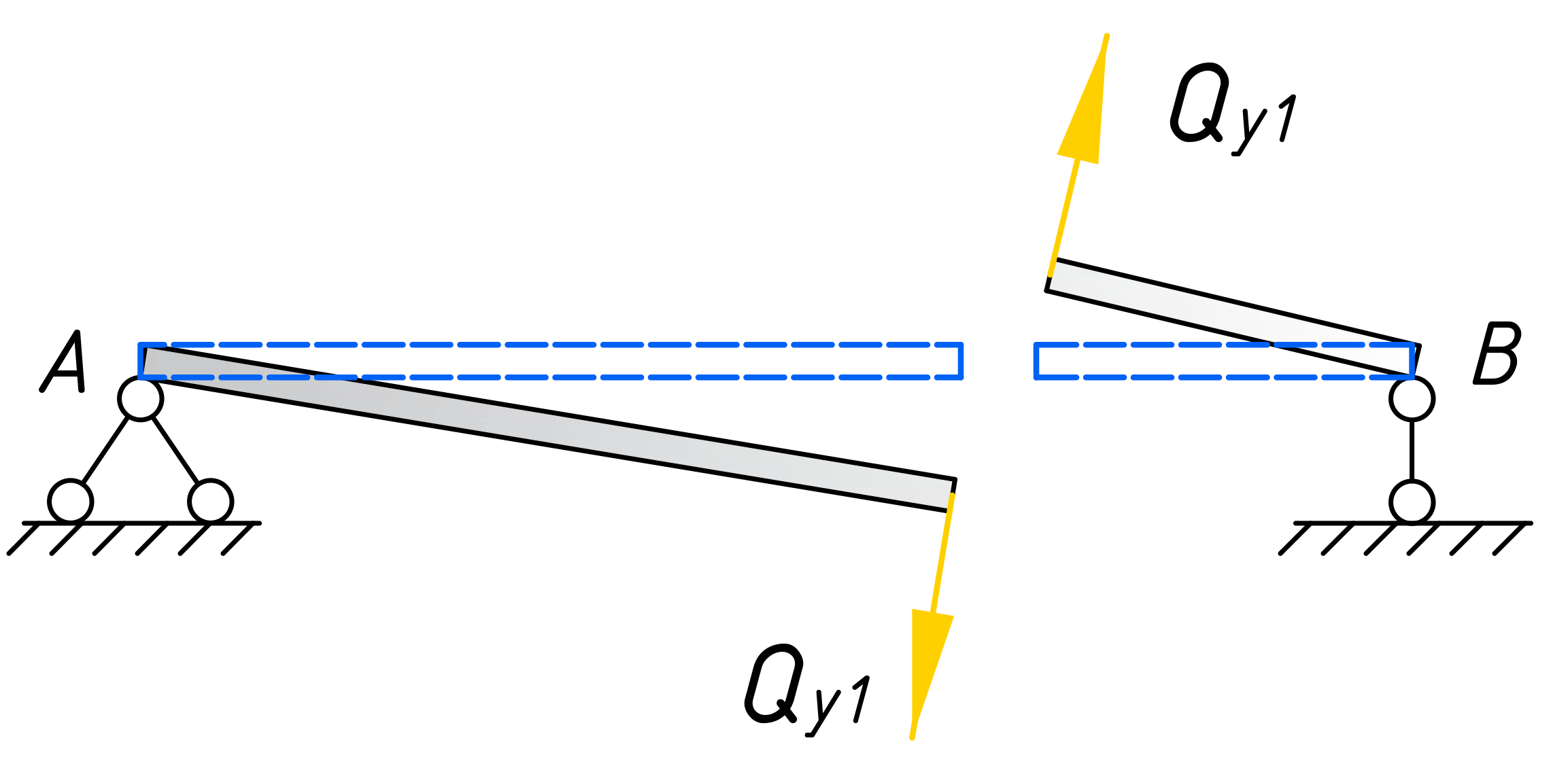
Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x1 от правого торца балки.
Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Qy1 и момента Mx1. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.
Правила знаков для поперечной силы
Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.
Также многие авторы рекомендуют просто запомнить такое правило:
Вводим систему координат для первого участка
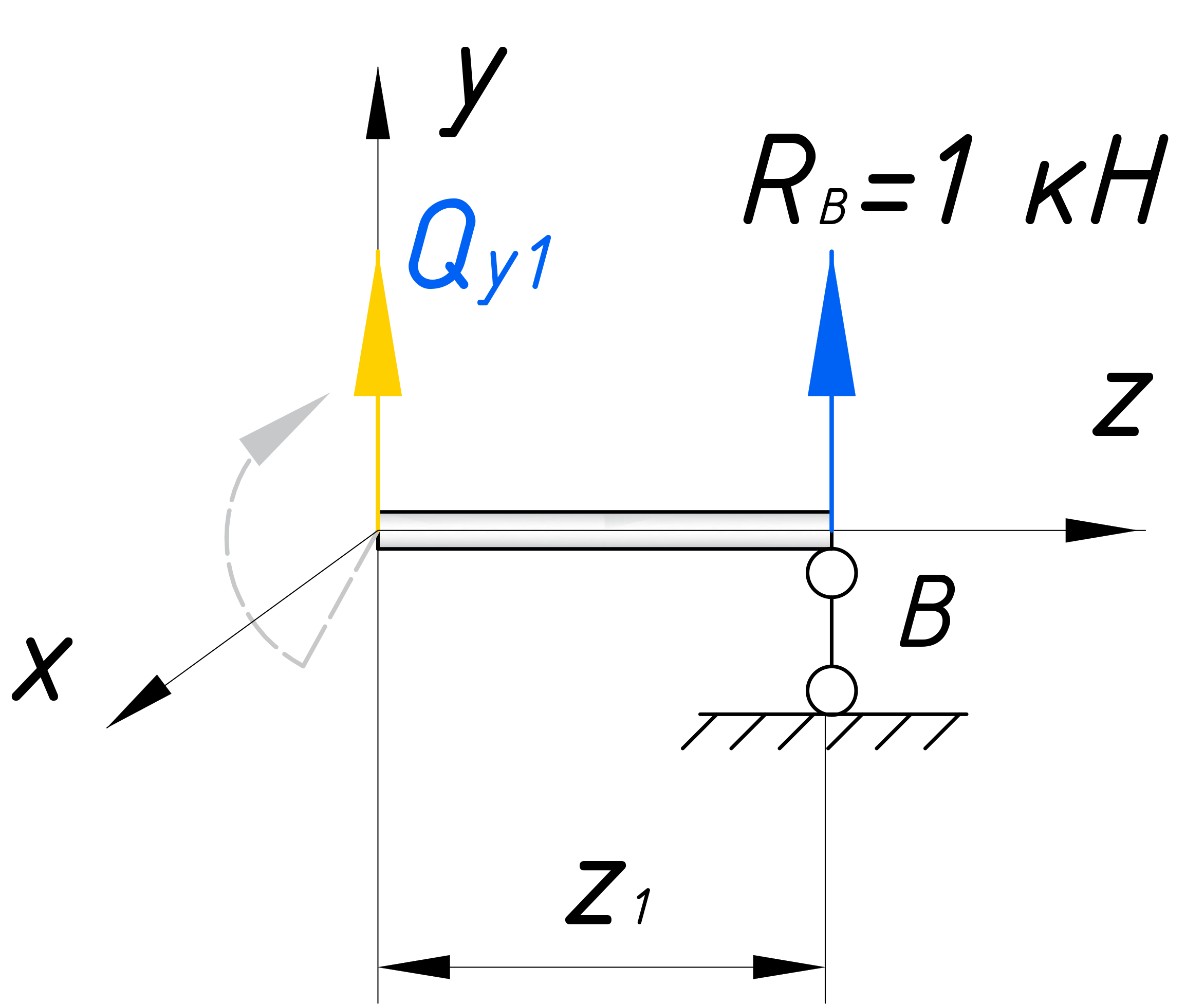
Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент Mx1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:
Записываем уравнение равновесия для первого участка и строим эпюру
Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:
Из полученного уравнения, следует:
Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:
Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.
Расчет второго участка
Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z2 от левого торца балки:
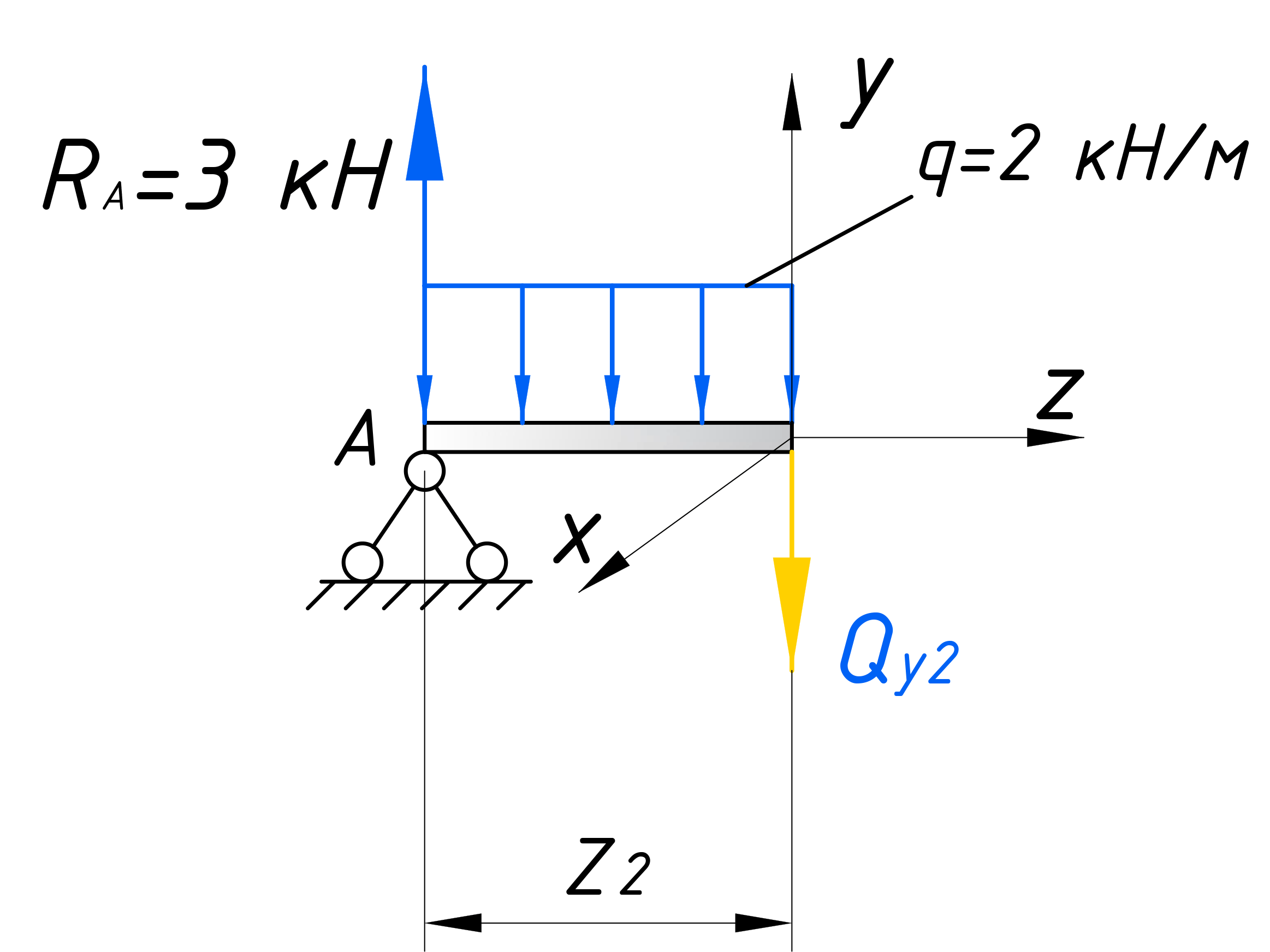
Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Qy2 и Mx2. Вводим локальную систему координат:
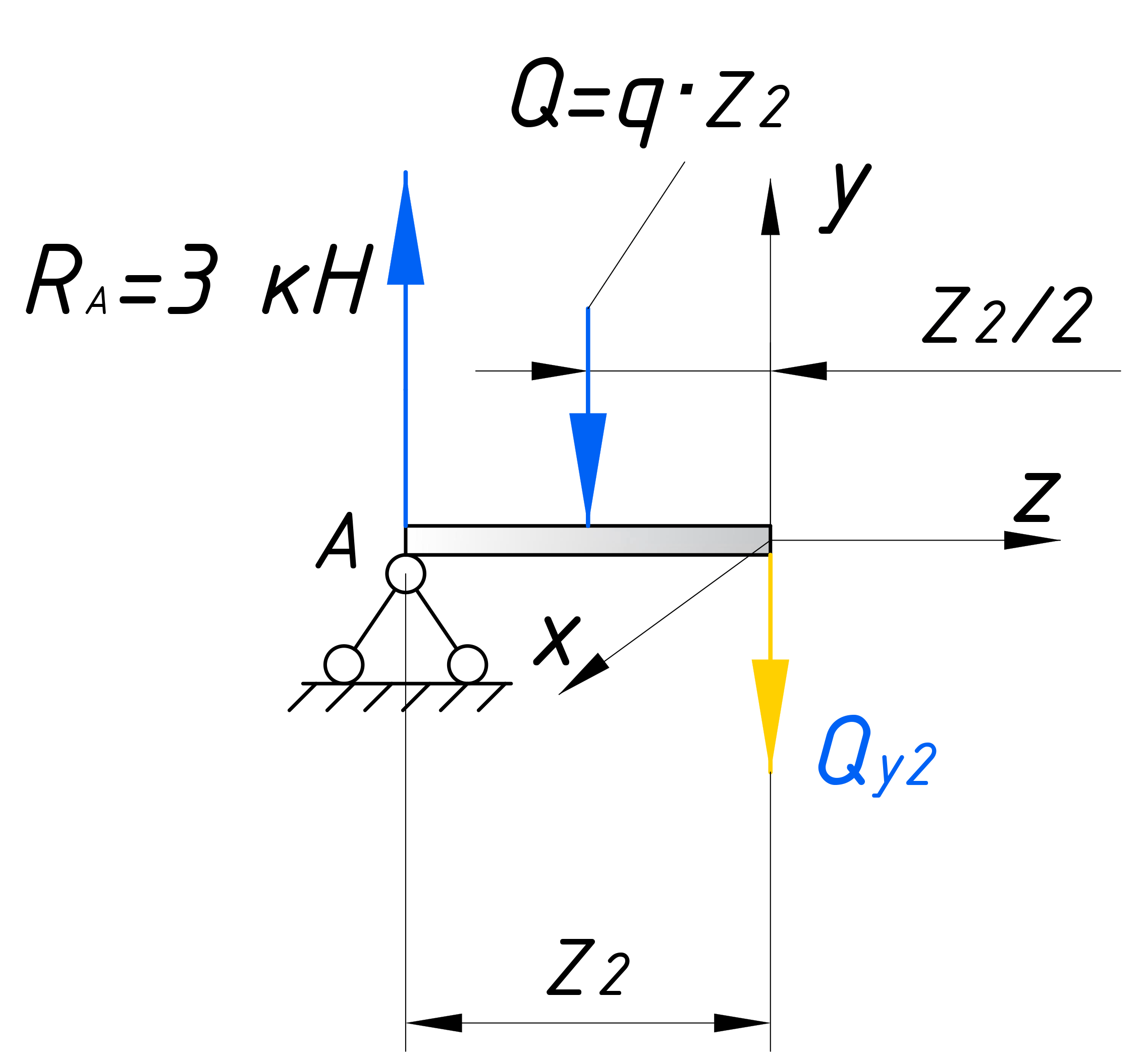
Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z2.
Записываем уравнение равновесия для второго участка:
Выражаем поперечную силу:
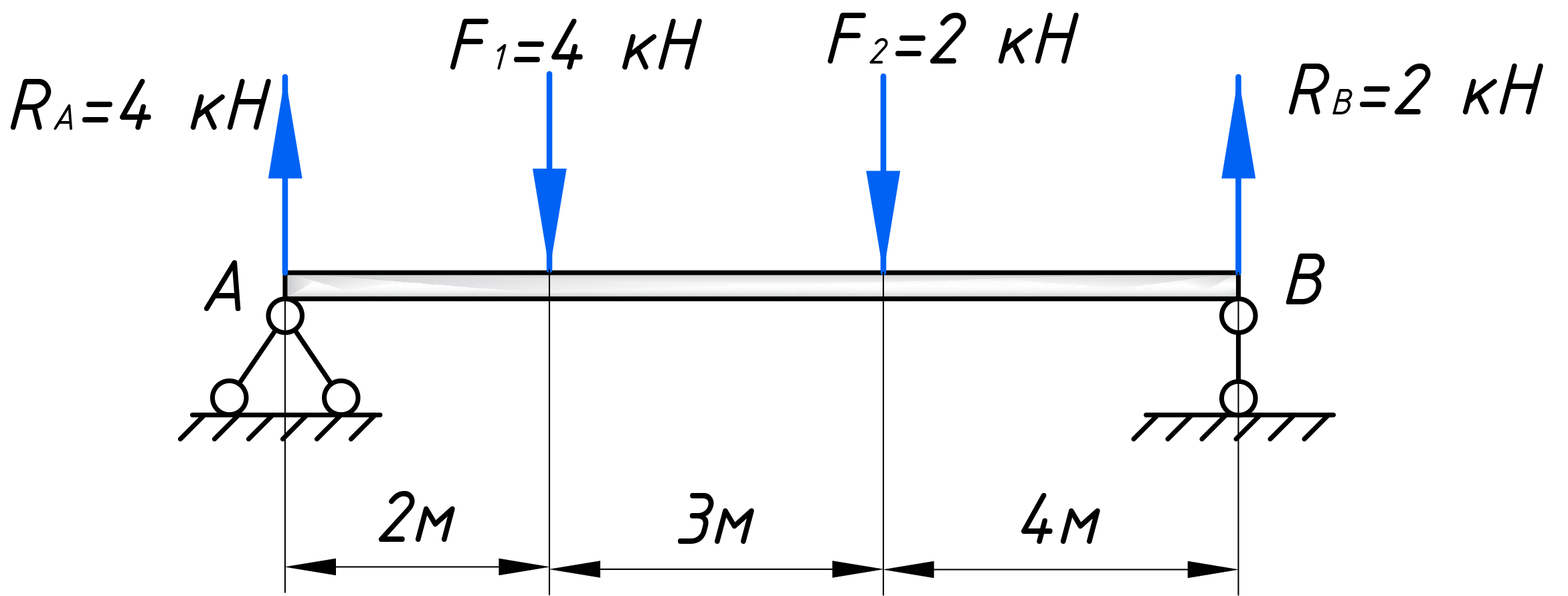
Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z2 подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z2=0) поперечная сила будет равна:
В середине пролета, при z2=2м получим:
По полученным значениям, строим эпюру поперечных сил на втором участке:
Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!
Упрощенный способ построения эпюры
Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учиться рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.
Первый участок
Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z1. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.
Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:
Как видно из уравнения, поперечная сила, на первом участке, не зависит от координаты z1, поэтому во всех сечениях она одинаковая.
Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.
Реакция RA, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:
Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернуться ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:
Подставляя численные значения нагрузки, получим следующий результат:
Теперь перейдем ко второму участку.
Второй участок
Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:
По выполненным расчетам двух участков, можно построить уже знакомую эпюру:
Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.
Быстрый способ построения эпюры
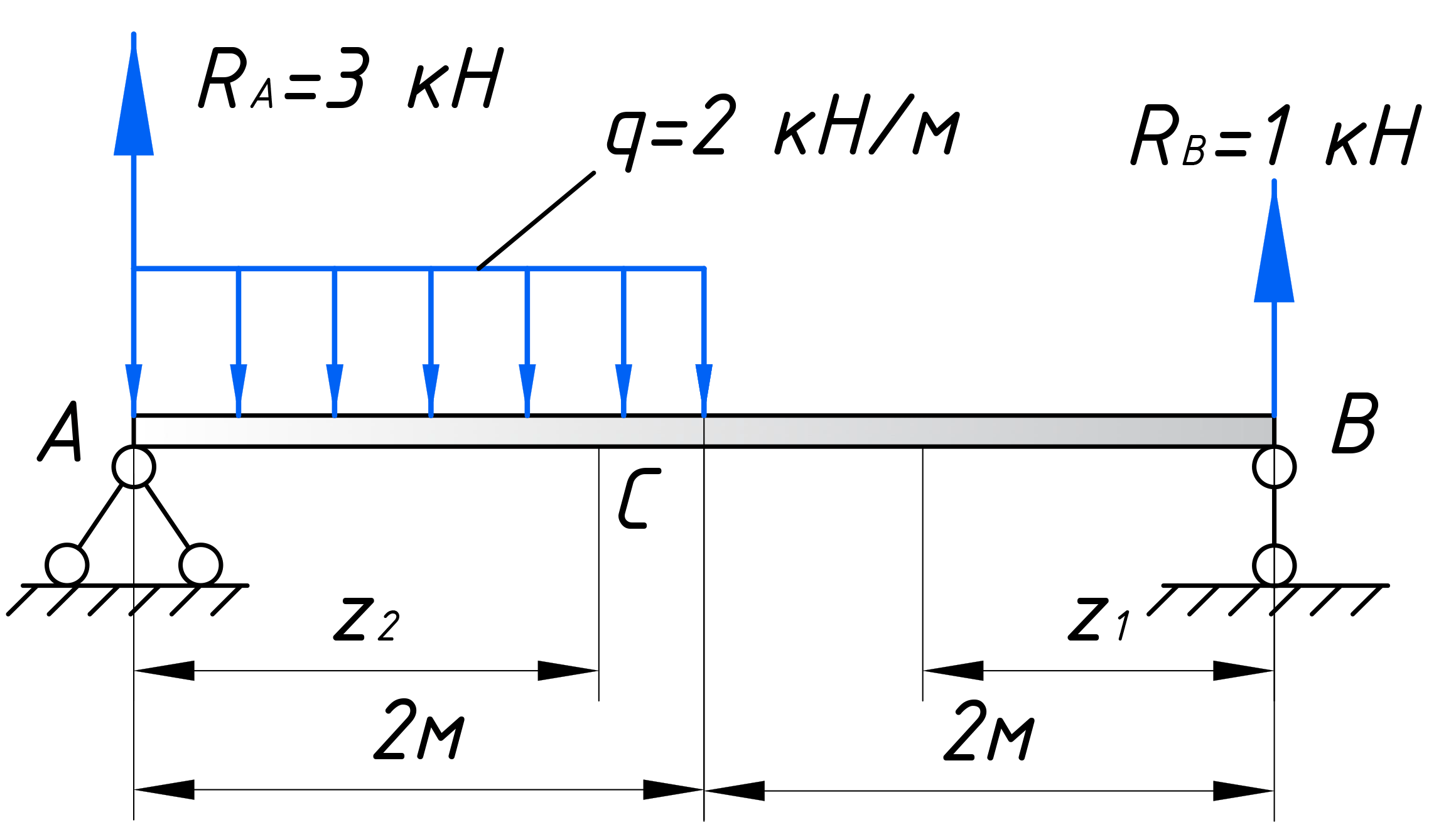
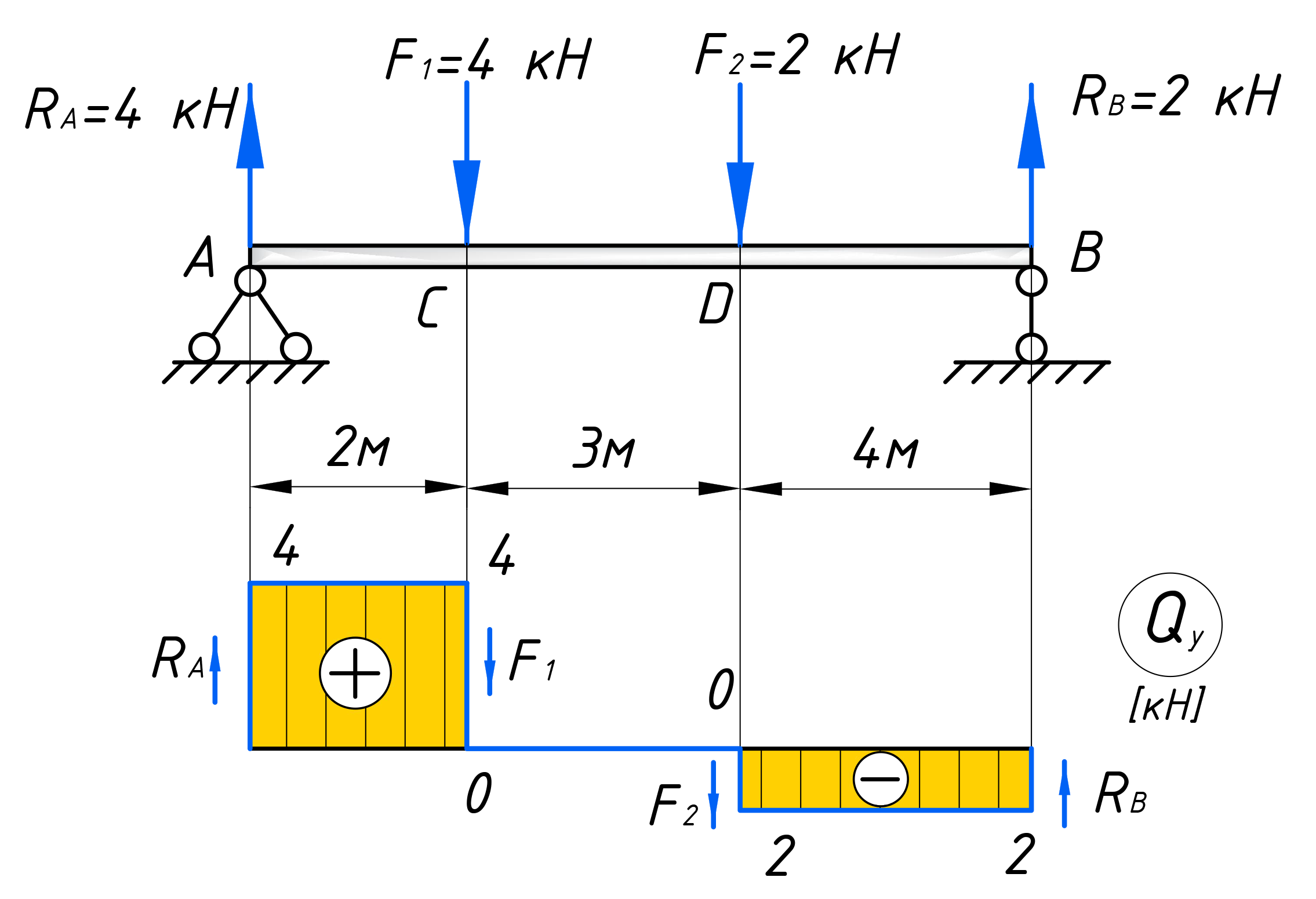
Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:
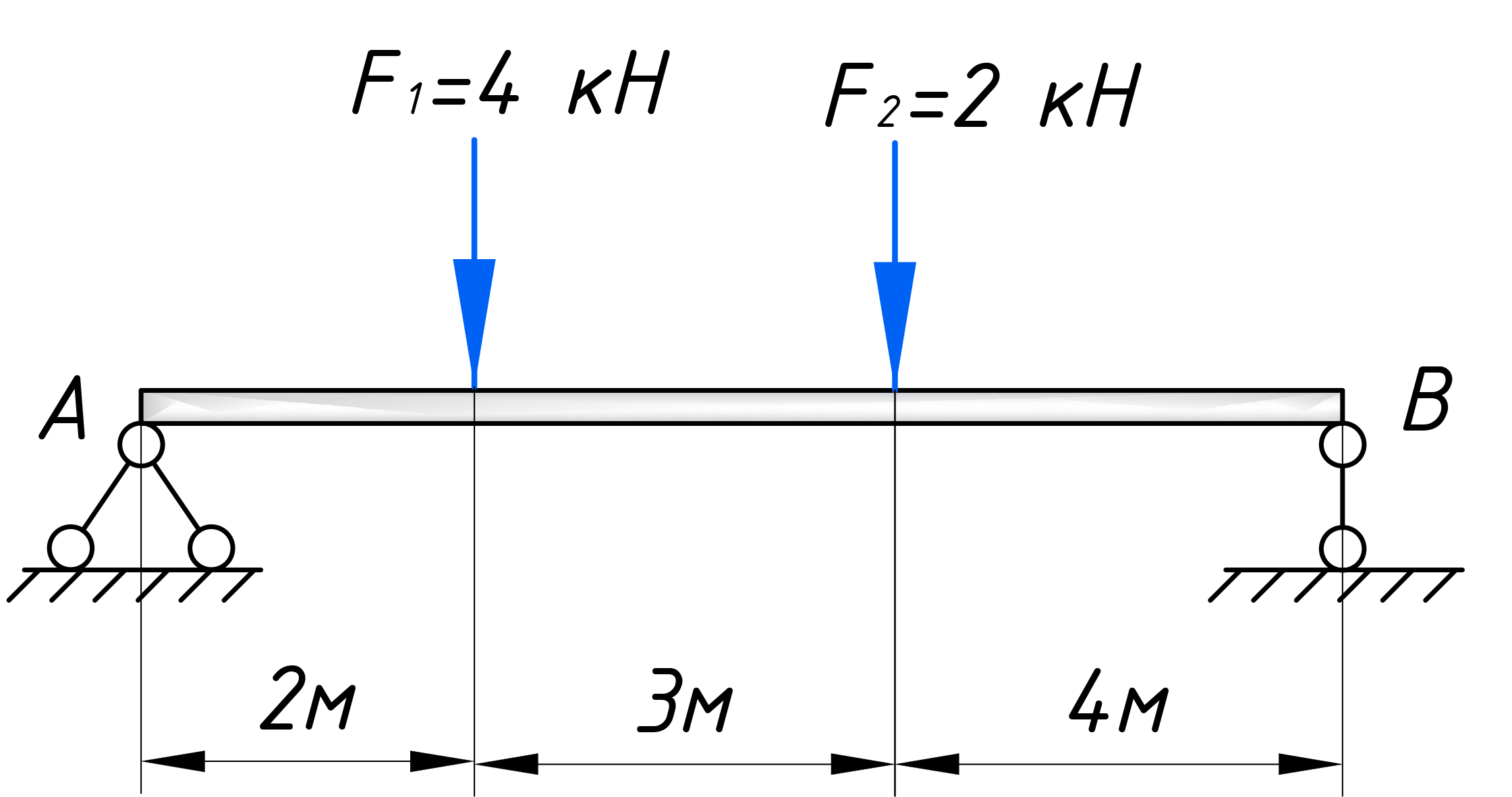
Определим для нее опорные реакции:
С учетом данных правил, получим вот такую эпюру поперечных сил:
Прокомментирую: в точке А, сила направлена вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направлена вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.
Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать насколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:
Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.
После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.