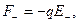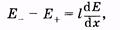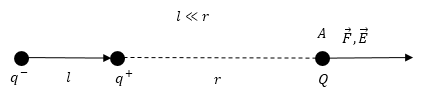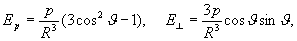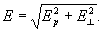Что такое электрический диполь

3.2. Электрический диполь

Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем.

Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6).

Рис. 3.6. Электрический диполь

Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)

Рис. 3.7. Линии напряженности электрического поля электрического диполя

Рис. 3.8. Эквипотенциальные поверхности электрического диполя

Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности

Основной характеристикой диполя является электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как

Рассмотрим поведение «жесткого» диполя — то есть расстояние которого не меняется — во внешнем поле Е (рис. 3.10).

Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле

Пусть направление дипольного момента составляет с вектором Е угол . На положительный заряд диполя действует сила, совпадающая по направлению с Е и равная F₁ = +qE, а на отрицательный — противоположно направленная и равная F₂ = –qE. Вращающий момент этой пары сил равен

Так как ql = р, то М = рЕ sin или в векторных обозначениях

(Напомним, что символ

означает векторное произведение векторов а и b.) Таким образом, при неизменном дипольном моменте молекулы () механический момент, действующий на нее, пропорционален напряженности Е внешнего электрического поля и зависит от угла между векторами р и E.

Под действием момента сил М диполь поворачивается, при этом совершается работа

которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле

если положить const = 0.

Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае , а, следовательно, и М = 0. С другой стороны, при потенциальная энергия диполя во внешнем поле принимает минимальное значение , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение. Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.

На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.

Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле

В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила F_paвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила F_paвн равна

Такой же результат может быть получен из общего соотношения

где энергия П определена в (3.8). Если Е увеличивается с ростом x, то

и проекция равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными.

Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.

На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.

Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор

Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.

Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора

В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как

где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов мы приходим к прежнему выражению

Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде

В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.

Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов

Введем теперь понятие «центр зарядов» — положительных R + и отрицательных R –

Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде

где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.

Дополнительная информация

Источник

Электрический диполь

Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя).

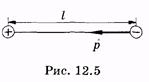
Основной характеристикой диполя (рис. 12.5) является его электрический момент (дипольный момент) — вектор, равный произведению заряда на плечо диполя l, направленный от отрицательного заряда к положительному:

(12.19)

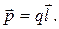
Единицей электрического момента диполя является кулон-метр. Поместим диполь в однородное электрическое поле напряженностью 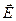(рис. 12.6).

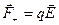
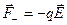
На каждый из зарядов диполя действуют силы и , эти силы равны по модулю, противоположно направлены и создают момент пары сил. Как видно из рисунка, он равен

М = qElsin a = pEsin a, (12.20) или в векторной форме 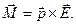. (12.21)

Таким образом, на диполь в однородном электрическом поле действует момент силы, зависящий от электрического момента и ориентации диполя, а также напряженности поля.

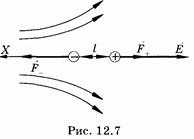
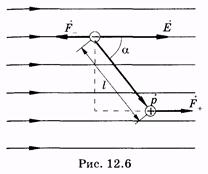
Рассмотрим теперь диполь в неоднородном электрическом поле. Предположим, что диполь расположен вдоль силовой линии (рис. 12.7). На него действуют силы

и

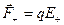
где Е₊ и Е_ — напряженности поля соответственно в месте нахождения положительного и отрицательного зарядов (на рис. 12.7 Е_— > Е₊). Значение равнодействующей этих сил

где dE/dx — производная от напряженности электрического поля по направлению оси ОХ, являющаяся мерой неоднородности электрического поля вдоль соответствующего направления. Из (12.23)следует, что

тогда формулу (12.22) можно представить в виде

(12.24)

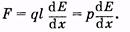
Итак, на диполь действует сила, зависящая от его электрического момента и степени неоднородности поля dE/dx. Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой линии, то на него дополнительно действует еще и момент силы. Таким образом, свободный диполь ориентируется вдоль силовых линий и втягивается в область больших значений напряженности поля.

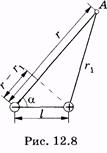
До сих пор рассматривался диполь, помещенный в электрическое по­ле, однако сам диполь также является источником поля. На основании (12.18) запишем выражение для электрического потенциала поля, со­зданного диполем, в некоторой точке А, удаленной от зарядов соответ­ственно на расстояния гиг, (рис. 12.8):

(12.25)

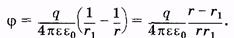
Обычно предполагают, что l

(12.28)

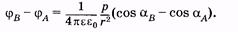
Учитывая эти равенства, выполним тригонометрические преобразования:

(12.29)

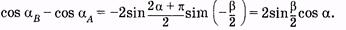
Подставляя (12.29) в (12.28), имеем

(12.30)

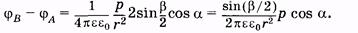
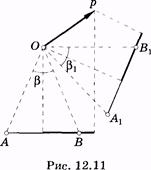
Как видно из (12.30), разность потенциалов двух точек поля диполя, равноотстоящих от него (при данных e и r), зависит от синуса половинного угла, под которым видны эти точки от диполя (рис. 12.10), и проекции электрического момента диполя р cos a на прямую, соединяющую эти точки (рис. 12.11). Эти замечания справедливы в рамках тех ограничений, которые были сделаны при выводе формулы (12.27).

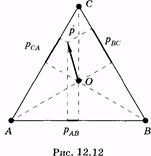
Пусть диполь, создающий электрическое поле, находится в центре равностороннего треугольника ABC (рис. 12.12). Тогда на основании (12.30) можно получить, что напряжения на сторонах этого треугольника относятся как проекции вектора 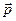на его стороны:

Источник

Электрический диполь

Вы будете перенаправлены на Автор24

Что такое электрический диполь

Электрическим диполем называется система из двух точечных зарядов, величина которых одинакова, но противоположна по знаку, при чем, эти точечные заряды разнесены на небольшое расстояние друг от друга. Вектор, соединяющий отрицательный заряд с положительным (направление от минуса к плюсу), называется плечом диполя.

Тогда векторная величина, равная:

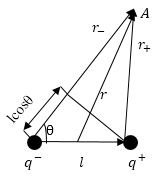
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:

При этом местоположение точки A можно характеризовать вектором$\overrightarrow<\ r>$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:

запишем формулу для напряженности поля диполя, которая будет иметь вид:

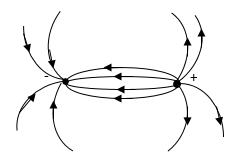
Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.

Модуль вектора сопряженности

В таком случае модуль вектора напряженности равен:

Вычисление момента сил

В однородном поле сила, которая действует на диполь со стороны поля ($\overrightarrow$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:

Момент этих сил равен:

Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$\ \overrightarrow=<\overrightarrow>_++<\overrightarrow>_-\ne 0$. В этом случае сила равна:

В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:

или, что то же самое, но короче:

Задание: Ответьте на вопрос: может ли точечный заряд двигаться с постоянной скоростью вокруг неподвижного точечного диполя?

Напряженность поля, которое создает диполь в точке А (где помещен заряд q) равна:

Тогда силу с которой поле диполя действует на заряд, который помещен в точку А найдем как:

\[F=Q\cdot E\ \left(2.3\right).\]

В результате получаем:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Источник

Диполь

(от Ди. и греч. pólos — полюс)

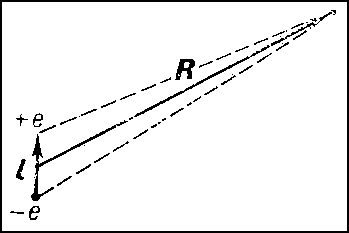
электрический, совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Основной характеристикой электрического Д. является его дипольный момент — вектор, направленный от отрицательного заряда к положительному (рис. 1) и численно равный произведению заряда е на расстояние l между зарядами: р = el. Дипольный момент определяет электрическое поле Д. на большом расстоянии R от Д. (R»l), а также воздействие на Д. внешнего электрического поля.

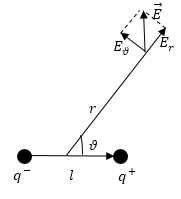
1/R 2 ). Компоненты напряжённости поля Е вдоль оси Д. (E_p) и в направлении, перпендикулярном к р (E_┴), пропорциональны дипольному моменту и в системе единиц СГС (Гаусса) равны:

где ϑ — угол между р и радиусом-вектором R точки пространства, в которой измеряется поле Д.; полная напряжённость

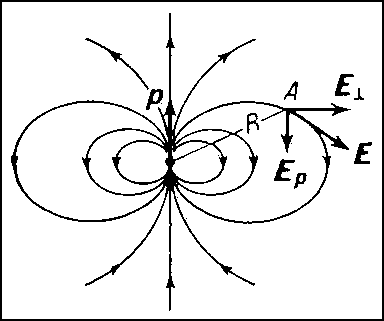
Т. о., на оси Д. при ϑ = 0 напряжённость поля вдвое больше, чем при ϑ = 90°; при обоих этих углах оно имеет только компоненту E_p, причём при ϑ = 0 её направление параллельно р, а при ϑ = 90° — антипараллельно (рис. 2).

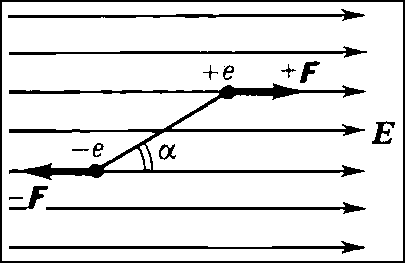
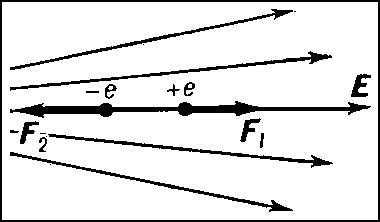
Действие внешнего электрического поля на Д. также пропорционально величине его дипольного момента. Однородное поле создаёт вращающий момент М = pE sinα (α — угол между вектором напряжённости внешнего электрического поля Е и дипольным моментом р; рис. 3), стремящийся повернуть Д. так, чтобы его дипольный момент был направлен по полю. В неоднородном электрическом поле на Д., кроме вращающего момента, действует также сила, стремящаяся втянуть Д. в область более сильного поля (рис. 4).

Электрическое поле любой нейтральной в целом системы на расстояниях, значительно больших её размеров, приближённо совпадает с полем эквивалентного Д. — электрического Д. с таким же дипольным моментом, как и у системы зарядов (т. е. поле на больших расстояниях от системы нечувствительно к деталям распределения зарядов). Поэтому во многих случаях электрический Д. является хорошим приближением для описания такой системы на больших по сравнению с её размерами расстояниях. Например, молекулы многих веществ можно приближённо рассматривать как электрический Д. (в простейшем случае это молекулы из двух ионов с зарядами противоположных знаков); атомы и молекулы во внешнем электрическом поле, несколько раздвигающем их положительные и отрицательные заряды, приобретают индуцированный (наведённый полем) дипольный момент и становятся микроскопическими Д. (см., например, Диэлектрики).

Электрический Д. с изменяющимся во времени дипольным моментом (вследствие изменения его длины l или зарядов e) является источником электромагнитного излучения (см. Герца вибратор).

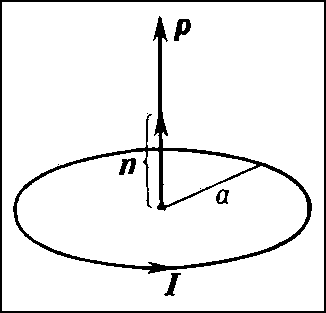
Д. магнитный. Исследование взаимодействий полюсов постоянных магнитов (Ш. Кулон, 1785) привело к представлению о существовании магнитных зарядов, аналогичных электрическим. Пара таких магнитных зарядов, равных по величине и противоположных по знаку, рассматривалась как магнитный Д. (обладающий магнитным дипольным моментом). Позднее было установлено, что магнитных зарядов не существует и что магнитные поля создаются движущимися электрическими зарядами, т. е. электрическими токами (см. Ампера теорема). Однако понятие о магнитном дипольном моменте оказалось целесообразным сохранить, поскольку на больших расстояниях от замкнутых проводников, по которым протекают токи, магнитные поля оказываются такими же, как если бы их порождали магнитные Д. (магнитное поле Д. магнитного на больших расстояниях от Д. рассчитывается по тем же формулам, что и электрическое поле Д. электрического, причём электрический момент диполя нужно заменить магнитным моментом тока). Магнитный момент системы токов определяется силой и распределением токов. В простейшем случае тока I, текущего по круговому контуру (витку) радиуса а, магнитный момент в системе СГС равен р = ISn/c, где S = πа 2 — площадь витка, а единичный вектор n, проведённый из центра витка, направлен так, что с его конца ток виден текущим против часовой стрелки (рис. 5), с — скорость света.

Аналогию между магнитным Д. и витком с током можно проследить и при рассмотрении действия магнитного поля на ток. В однородном магнитном поле на виток с током действует момент сил, стремящийся ориентировать виток так, чтобы его магнитный момент был направлен по полю; в неоднородном магнитном поле такие замкнутые токи («магнитные Д.») втягиваются в область с бо́льшей напряжённостью поля. На взаимодействии неоднородного магнитного поля с магнитным Д. основано, например, разделение частиц с различными магнитными моментами — ядер, атомов или молекул (магнитные моменты которых обусловлены движением входящих в их состав заряженных элементарных частиц, а также магнитными моментами, связанными со Спинами частиц). Пучок частиц, проходя через неоднородное магнитное поле, разделяется, т.к. поле сильнее изменяет траектории частиц с большим магнитным моментом.

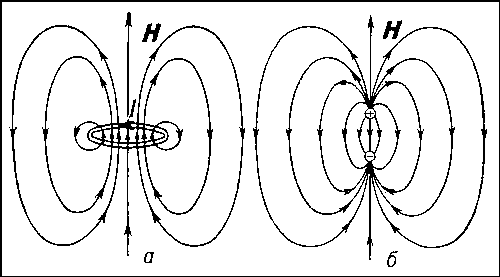
Однако аналогия между магнитным Д. и витком с током (теорема эквивалентности) не является полной. Так, например, в центре кругового витка напряжённость магнитного поля не только не равна напряжённости поля «эквивалентного» Д., но даже противоположна ей по направлению (рис. 6). Магнитные силовые линии (в отличие от электрических силовых линий, которые начинаются и кончаются на зарядах) являются замкнутыми.

Лит.: Фейнман P., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, в. 5. Электричество и магнетизм, [пер. с англ.], М., 1966, гл. 6; Калашников С. Г., Электричество, М., 1956, § 17 (Общий курс физики, т. 2); Киренский Л. В., Магнетизм, 2 изд., М., 1967; Тамм И. Е., Основы теории электричества, 7 изд., М., 1957.

Г. Я. Мякишев, В. И. Григорьев.

Рис. 2. Электрическое поле диполя, изображенное с помощью силовых линий. В точке наблюдения А, находящейся на расстоянии R от центра диполя (R>>l), поле Е (направленное по касательной к силовой линии) разложено на 2 компоненты: E_p — параллельную оси диполя и E — перпендикулярную к ней.

Рис. 3. На диполь в однородном внешнем электрическом поле Е действует пара сил (-F, +F), которая создаёт вращающий момент, стремящийся повернуть диполь в направлении поля.

Рис. 5. Магнитный момент кругового тока.

Рис. 6. Магнитное поле вблизи кругового тока I (а) и магнитного диполя (б); на больших расстояниях поля́ одинаковы.

Источник