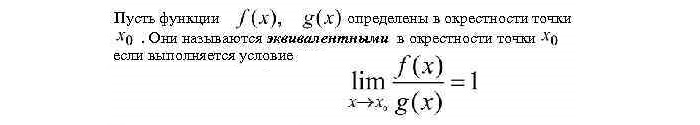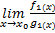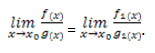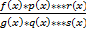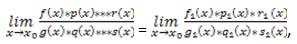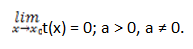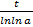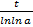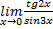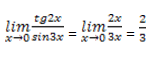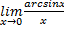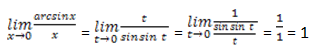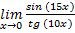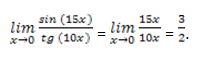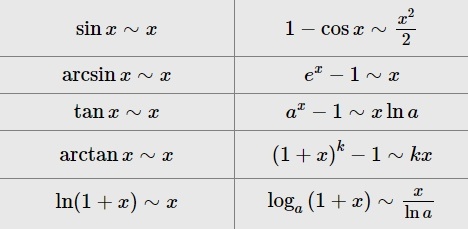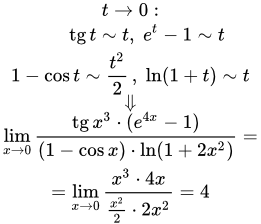Что такое эквивалентные функции определение

18.12.202310.07.2022 admin 0 Comments

В данной статье речь пойдет об основных понятиях эквивалентных функций, с помощью которых можно найти значение пределов. Понятие эквивалентности поменяется не только в высшей математике, но и в логике, психологии, при переводах с иностранных языков. Оно означает «равнозначность», «равносильность», «равенство».

Определение эквивалентных функций

Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.

Теорема о замене функций эквивалентными в пределе частного

Если при x₁, стремящимся к x₂, f(x)

g₁(x) существует предел:

то существует и предел:

Доказательство

Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:

в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:

Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.

Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.

Таблица эквивалентных функций

Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x₀:

Эквивалентность при t → 0

Равенство при t → 0

a t – 1 = t ln a + 0(t)

Всегда ли можно сделать замену функций эквивалентными?

Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.

В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.

Примеры решения пределов с помощью эквивалентных функций

Для сравнения рассмотрим несколько примеров.

Пример 1

Начнём решение, учитывая, что tg2x

Пример 2

Пусть arcsin x = t, тогда x = sin t и t → 0 при x → 0. Исходя из этого:

Пример 3

Решение: если sin (15x)

Для решения пределов можно использовать онлайн калькуляторы, размещенные на ресурсах в свободном доступе.

Источник

Эквивалентные функции

Что такое эквивалентные функции

Эквивалентность — равнозначность в каком-либо отношении.

Эквивалентные функции позволяют облегчить процесс вычисления пределов с помощью замены множителей в примерах с дробями и произведениями.

Функции α(x) и β(x) называются эквивалентными при x→α, если \( \lim_\frac<\alpha(x)><\beta(x)>=1.\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Данное определение применимо к бесконечно большим и малым функциям.

Эквивалентность обозначается знаком ∼, т.е. чтобы показать, что функции α(x) и β(x) эквивалентны, нужно оформить запись следующим образом: α(x)∼β(x)

Для удобства следует использовать специальную таблицу.

Эквивалентные функции и их применение к нахождению пределов

Свойства функций

Основные свойства бесконечно малых функций:

Основные свойства эквивалентных бесконечно больших функций:

Применяемые определения

Данных определений будет достаточно для решения пределов с применением понятия эквивалентности.

Применяемые теоремы

Теорема 1 (о замене эквивалентными в произведении и отношении):

Теорема 2:

Теорема 3:

Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Теорема 4:

Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Теорема 5 (о замене эквивалентных функций в пределах частного):

Сравнение функций

Сравнение бесконечно малых функций

Сравнение бесконечно больших функций

Примеры решения пределов с помощью эквивалентных функций

Воспользуемся таблицей эквивалентных функций.

Произведем замену переменной

\((x-\mathrm\pi)=y, где y\rightarrow0, если x\rightarrow\mathrm\pi\)

Применим формулу приведения:

Воспользуемся таблицей эквивалентных функций.

Источник

Эквивалентные функции определение, формулы, основные свойства, доказательство теоремы о замене функций, примеры нахождения пределов, таблица

В данной статье речь пойдет об основных понятиях эквивалентных функций, с помощью которых можно найти значение пределов.

Понятие эквивалентности поменяется не только в высшей математике, но и в логике, психологии, при переводах с иностранных языков. Оно означает «равнозначность», «равносильность», «равенство».

Определение эквивалентных функций

Эквивалентные функции — это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.

Теорема о замене функций эквивалентными в пределе частного

Если при x1, стремящимся к x2, f(x)

g1(x) существует предел:

то существует и предел:

Доказательство

в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:

Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.

Таблица эквивалентных функций

Источник

Применение эквивалентных функций при решении пределов

Метод решения

Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).

Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.

Применяемые определения и теоремы

Таблица эквивалентных функций

Эквивалентность при

Равенство при

Предостережение

Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.

Пример 1

Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 2

Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 3

Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;

Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 4

В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.

Теперь заменим множители эквивалентными функциями:
.

Примечание. Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили \ln (1+x) на x, то получили бы ошибку.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Источник

09.5. Эквивалентные функции

В тех случаях, когда функциональная зависимость имеет довольно сложный вид, возникают большие трудности при изучении ее свойств. Простой просчет значений функции на ЭВМ порой может оказаться неосуществимым, так как даже современные ЭВМ допускают значительные погрешности в расчетах с очень большими или же малыми числами. Мы рассмотрим весьма интересный подход к изучению функциональных зависимостей, основанный на их замене более простыми функциями в окрестности некоторых предельных точек.

Будем говорить, что функции и ЭКВИВАЛЕНТНЫ в окрестности предельной точки (конечной или бесконечной), если найдется такая функция в окрестности этой предельной точки, что