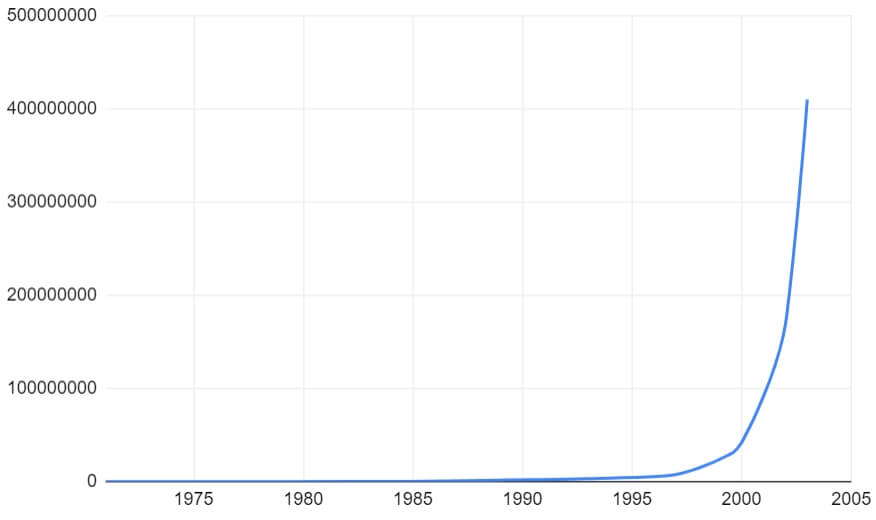Что такое экспоненциальная скорость
Экспоненциальный рост
Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону. Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейному, степенному или геометрическому зависимостям.
Содержание
Свойства
Для любой экспоненциально растущей величины, чем большее значение она принимает, тем быстрее растет. Также это означает, что величина зависимой переменной и скорость ее роста прямо пропорциональны. Но при этом, в отличие от гиперболической экспоненциальная кривая никогда не уходит в бесконечность за конечный промежуток времени.
Экспоненциальный рост в итоге оказывается более быстрым, чем любая геометрическая прогрессия, чем любой степенной, и тем более, чем любой линейный рост.
Математическая запись
Экспоненциальный рост описывается дифференциальным уравнением:
Решение этого дифференциального уравнения — экспонента:
Примеры
Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов. Другим примером экспоненциального роста являются сложные проценты.
См. также
Ссылки
Полезное
Смотреть что такое «Экспоненциальный рост» в других словарях:
экспоненциальный рост — eksponentinis didėjimas statusas T sritis fizika atitikmenys: angl. exponential rising vok. Exponentialanstieg, m rus. экспоненциальный рост, m pranc. accroissement exponentiel, m … Fizikos terminų žodynas
ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ — рост с относительно постоянной скоростью … Словарь ботанических терминов
Рост — процесс увеличения какого либо качества со временем. Качества могут быть как физическими (например, рост в высоту), так и абстрактными (например, взросление человека, расширение системы): Клеточный рост, или пролиферация Рост населения Рост… … Википедия
Закон экспоненциального роста — Экспоненциальный рост в математике экспоненциальное возрастание величины (возрастание в геометрической прогрессии), которая растет со скоростью, пропорциональной её значению. Говорят что такой рост подчиняется экспоненциальному закону. Это… … Википедия
АЛГОРИТМ — [от algorithm!; algorismus, первоначально лат. транслитерация имени ср. азиат. учёного 9 в. Хорезми (Мухаммед бен Муса аль Хорезми)], программа, определяющая способ поведения (вычисления); система правил (предписаний) для эффективного… … Философская энциклопедия
ДИОФАНТОВЫХ УРАВНЕНИИ ПРОБЛЕМА РАЗРЕШИМОСТИ — проблема отыскания алгоритма для распознавания по любому диофантову уравнению, имеет ли оно решение. Существенным в постановке проблемы является требование найти универсальный метод, к рый должен быть пригоден для любого уравнения (все известные… … Математическая энциклопедия
Перцептрон — Логическая схема перцептрона с тремя выходами Перцептрон, или персептрон[nb 1] (англ. perceptron от … Википедия
Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е» – это число Эйлера, которое представляет собой постоянную (
2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.
Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).
Экспонента в жизни. Экспоненциальный рост
Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.
Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.
Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.
Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.
Чем экспоненциальный рост отличается от линейного?
Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.
В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.
При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.
Экспоненциальный рост
Журналисты, блогеры и диванные эксперты… Все используют фразы «экспоненциальный рост», а кто по проще «рост по экспоненте». Кое-кто, наверное, даже помнит, что такое экспонента, но вряд ли сможет объяснить простыми словами. Что же, пришла пора разобраться то, чем мы так часто пользуемся. Возможно, все совсем не так…
Экспонента
Здесь все просто (но это только пока). Многие считают, что экспонента это просто число е=2,718281828459045235360287. Конечно, это не так. Это самое число e, называется числом Эйлера, оно трансцендентно и иррационально, что звучит красиво и загадочно, но экспонента, не число, а функция.
Те, кто немного дружил с математикой в школе сразу заметят интересную особенность этой функции. Ее основанием является не отрицательное число, а значит, она будет всегда возрастать.

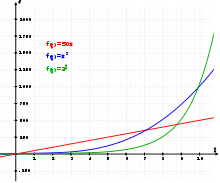
При х=0 у=1, при х=1, у=2,718, при х=2 y=7,39…. Ну а при х=10, у=22 026,5
Значение функции растет и растет явно очень быстро. Стремительно и неудержимо.
Экспоненциальный рост
Что такое экспоненциальный рост? Простыми словами, это такой рост, при котором, чем больше вырастят какое-либо значение, тем больше ускоряется его рост. То есть, со временем растет не только значение, но и сама скорость его роста.
А это, иными словами, означает, что значение переменной функции и скорость ее роста находятся в прямо пропорциональной зависимости. То есть, если значение увеличиться два раза, скорость роста увеличится тоже в 2 раза.
В конечном итоге, экспоненциальный рост — самый быстрый.
На самом деле, все вышесказанное касается любой показательной функции, а не только экспоненты.
Основанием может быть любое не отрицательное число, хоть два, хоть три, хоть… сколько угодно.
Несколько примеров из жизни
Самым актуальным и наглядным можно назвать ситуацию с распространением вируса (либо любой другой инфекции). Предположим, что каждый человек в течение дня заражает двух других. Тогда, в первый день у нас будет один инфицированный, во второй — трое. Один старый знакомый и два новых. Каждый из новичков, в свою очередь заразит двух других. В третий день — 7 заразившихся, в четвертый — 1, а пятый — 31… Стоп, это только при условии, что каждый человек заразит только двоих и, чудесным образом, перестанет это делать на притяжении следующих дней. Но ведь так не будет! Все эти люди и дальше будут заражать по 2 человека в день.
А раз так, то на третий день будет уже 9 разносчиков вируса, на пятый — 81, а через неделю по нашему воображаемому городу будет бродить уже 729 зараженных.
Это и будет экспоненциальный рост количества зараженных. Без учета их лечения, карантина или любых других мер, болезнь будет развиваться именно так. Через 10 дней зараженных людей будет уже 59 тысяч человек. Через 15 дней — более 14 миллионов. Просто математика, но какой яркий пример экспоненциального роста?
Легко вывести формулу: 1, 3, 9, 27, 81… это «три» в степени 2, 3 и 4. То есть, показательна функция с основанием 3.
И, хотя в этой формуле в степень возводится не число Эйлера (2,71828….), такой рост тоже называется экспоненциальным.
Еще один пример из биологии: размножение бактерий.
Бактерии размножаются делением. Каждая делится надвое и так далее… Но, конечно, не бесконечно. Предел есть, но об этом чуть позже.
Экспоненциальный рост в экономике
Есть примеры роста по экспоненте и в экономике. Самый интересный — финансовая пирамида. Самый безопасный — Закон Мура.
Первый закон Мура гласит, что количество транзисторов удваивается каждые 2 года. Таким образом и вычислительные мощности компьютера удваиваются каждые два года.
Второй Закон Мура (который сформулировал уже не Гордон Мур) гласит, что стоимость производства микросхем также возрастает экспоненциально из-за усложнения технологий.
Что же касается финансовых пирамид, то основная идея в том, что их рост обусловлен исключительно ростом количества «сектантов» верящих в огромные прибыли или тех, кто верит, что сумеет вовремя «соскочить». Так или иначе, пирамиды всегда рушатся. И вот вопрос, почему?
Но, конечно, рост не может продолжаться бесконечно. В случае с бактериями (и любыми другими организмами, да хоть мышами), наступит время, когда им не хватит пространства и пищи. В случае с микросхемами наступит физический предел скорости передачи данных (мы вряд ли сумеем превысить скорость света). Ну а всевозможные волшебные экономические модели в форме пирамид рано или поздно сталкиваются с той же проблемой, питательная среда в виде легковерных последователей
Логистическая кривая
В реальном мире, не таком идеальном как математика, любой процесс может столкнутся с пределом. В примере роста популяции бактерий или даже крупных животных, это количество ресурсов, которое всегда ограничено. Поэтому, при условии, что ресурсы не бесконечны, процесс развивается по s образной кривой. Сначала стремительно растет, а потом — замедляется.
В пример с вирусом, наступает день, когда большая часть населения уже переболела и выработала антитела (либо была искусственно привита) и вирус больше не может распространяться по экспоненциальному закону. Главный вопрос, можно ли точно предсказать этот день?
Мальтузианская ловушка
С экспонентой связан еще один занимательный экономический эффект — «мальтузианская ловушка». Представьте, что рост населения страны происходит по экспоненциальному закону. Например, каждая пара производит на свет не менее 4 детей, те в свою очередь поступают также. Рано или поздно, количество людей превысит количество пищи, необходимое для нормальной жизни.
Просто потому, что производительность труда физически ограничена (например, количеством плодородных земель), к тому же развитие технологий чаще всего происходит линейно, а экспонента всегда растет быстрее. Получается, что технологическое развитие общества не успевает за ростом населения.
Чем это заканчивается? Кризисом, голодом, войнами за ресурсы. Население уменьшается и все начинается с начала.
Почему это сложно представить?
Нам, людям, сложно себе представить развитие процесса «по экспоненте» потому, что не свойственно так мыслить. Мы привыкли к линейным и циклическим процессам. Они чаще встречаются в нашей жизни: циклические изменения дня и ночи и линейные изменения времени. Это просто и привычно. А вот экспоненциальные процессы встречаются реже.
Тем не менее они есть и игнорировать их опасно. Просто потому, что за этой скоростью нашему разуму сложно угнаться. Даже простые объяснения экспоненциального роста кажутся чем-то абстрактным, а ведь это не выдумка, а наша реальность.
Экспоненциальный рост
Если прирост численности популяции пропорционален количеству особей, численность популяции будет расти экспоненциально.
Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.
Экспоненциальный рост имеет место в тех популяциях, в которых прирост численности (число рождений минус число смертей) пропорционален числу особей популяции. Для популяции человека, например, коэффициент рождаемости примерно пропорционален количеству репродуктивных пар, а коэффициент смертности примерно пропорционален количеству людей в популяции (обозначим его N ). Тогда, в разумном приближении,
(Здесь r — так называемый коэффициент пропорциональности, который позволяет нам записать выражение пропорциональности в виде уравнения.)
Пусть d N — число особей, добавившихся к популяции за время dt, тогда если в популяции в общей сложности N особей, то условия для экспоненциального роста будут удовлетворены, если
После того как в XVII веке Исаак Ньютон изобрел дифференциальное исчисление, мы знаем, как решать это уравнение для N — численности популяции в любое заданное время. (Для справки: такое уравнение называется дифференциальным.) Вот его решение:
где N 0 — число особей в популяции на начало отсчета, а t — время, прошедшее с этого момента. Символ е обозначает такое специальное число, оно называется основание натурального логарифма (и приблизительно равно 2,7), и вся правая часть уравнения называется экспоненциальная функция.
Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.
Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу. В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль, как я говорю моим студентам, такова: иногда не следует быть чересчур умным!
d N = rN(1 — ( N / K )) dt
Обманчивый мир технологий. Или экспоненциальный рост для «чайников»
Сегодня мы поговорим об экспоненциальном росте…
Стойте, не уходите! Я понимаю, звучит так, будто это не очень интересно и не совсем то, чего ожидаешь от сайта о мобильных технологиях. Но я вас уверяю, вы заблуждаетесь! Речь пойдет именно о том, о чем вам, как любителю современных технологий, точно хотелось бы знать.
Дело в том, что мы не совсем корректно понимаем многие процессы по той причине, что не можем осознать экспоненциальный рост (проще говоря, геометрическую прогрессию). Нет, логикой-то мы всё хорошо понимаем, но вот с осознанием как-то не складывается (вспомните легенду о зернах на шахматной доске).
Из-за этого получается такой парадокс — мы удивляемся, как быстро человечество перешло от калькуляторов к дополненной реальности (AR) и в то же время не видим дальше собственного носа, когда речь заходит о будущем.
После прочтения этой статьи, вы совершенно по-другому посмотрите на свой смартфон и на то, чем он может стать в скором времени!
Иллюзия прогресса, или что такое экспоненциальный рост
Если говорить простым языком, то экспоненциальный рост — это когда скорость роста какой-то величины зависит от ее размера. То есть, чем больше становится какое-то значение, тем быстрее оно растет. Снежный ком — неплохой пример экспоненциального роста.
Вроде бы все понятно, о чем тут еще говорить? Ну что ж, давайте проверим, так ли это.
Иллюзия обмана
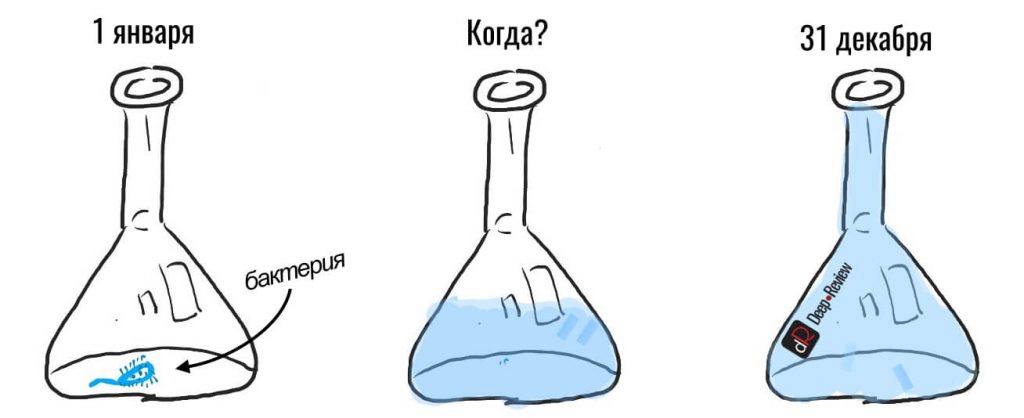
Вот у вас есть колбочка, в которую вы поместили одну бактерию. Число бактерий в колонии всегда растет экспоненциально. То есть, каждая бактерия делится на две, затем уже эти две делятся еще на две и получается четыре бактерии и так далее. Чем больше бактерий, тем быстрее будет расти их количество.
Предположим, что одна бактерия будет делиться на две ровно за один день. А вся колба заполнится бактериями за год, то есть, 31 декабря в колбе не останется больше места.
Внимание, вопрос! Если 1 января в колбе была 1 бактерия, а 31 декабря она заполнилась доверху, в какой день колба была заполнена ровно наполовину?
Наше «линейное» мышление всячески противится верному ответу: колба была заполнена на половину 30 декабря, ровно за 1 день до того, как места в ней больше не осталось.
И правда, если каждая бактерия 30 декабря разделится на две (то есть, произойдет то, что и происходило каждый день), то количество бактерий удвоится и, соответственно, полупустая колба заполнится.
Что же это получается? За целый год (без одного дня) мы с трудом собрали пол колбы бактерий, а на заполнение второй половины ушел всего день? Кажется, произошел взрывной рост!?
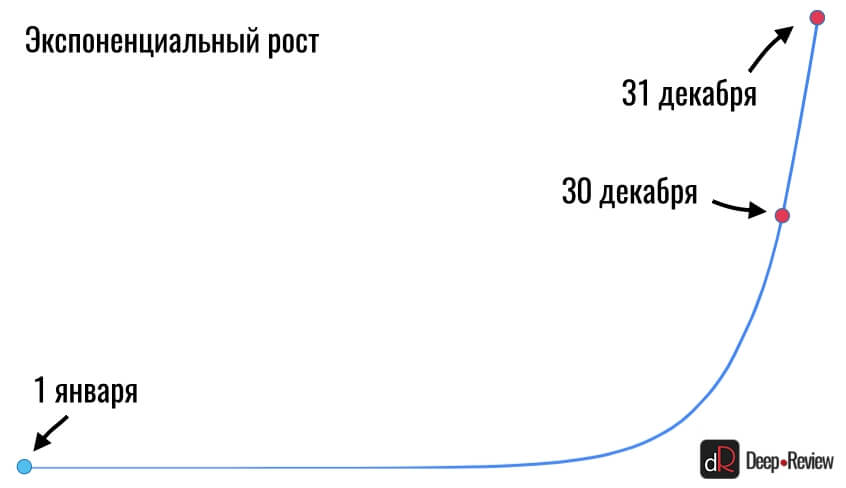
Вот как бы это все примерно выглядело на графике:
Ну вот мы и попались в ловушку! Ведь никакого взрывного роста под конец года не было. Темпы роста сохранялись на одном уровне в течение всего года — каждые день количество бактерий удваивалось.
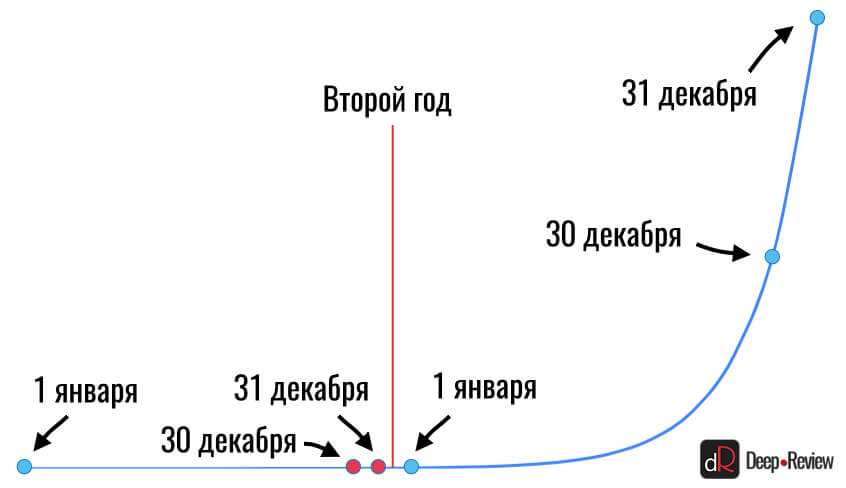
И теперь самое интересное! Если бы рост бактерий продолжился еще в течение следующего года, как вы думаете, где бы оказались наши точки 30 и 31 декабря? А вот где (показано красным цветом):
Как вам такое? Что же это теперь получается, на самом деле никакого взрывного роста в конце первого года не было? Ведь на графике эти точки находятся на прямой линии, а реальный рост начался ближе к концу второго года…
Я думаю, не нужно объяснять, что будет, если мы дальше продолжим наблюдать рост. Верно, кривая останется прежней, а наши «взрывные темпы роста» будут смещаться влево и превращаться в прямую линию. И каждый раз мы будем видеть одно и то же — ничего не росло в течение всего времени, а под конец — взрывной рост, пик, апогей!
«Как же нам повезло жить на пике технологий!»
Наверное, каждого посещали такие мысли. Ну правда, посмотрите, как человечество топталось на месте последние 40-50 лет и что произошло затем:
Согласен, график немножко спекулятивный, так как он показывает рост количества транзисторов в микропроцессорах, а это не совсем то же, что и рост производительности. Тем не менее, связь есть и мы ее прекрасно наблюдаем. Даже по своим смартфонам, сердцем которых и являются эти микропроцессоры.
А еще вы заметили, что красный график в точности повторяет экспоненциальную кривую, которую мы рассматривали на примере бактерий. То есть, можно смело утверждать, что последние 50 лет транзисторы уменьшались в размерах по экспоненциальной кривой. А из этого уже можно делать определенные выводы.
Когда современный молодой человек посмотрит на этот график, он ужаснется тому, как медленно развивались технологии с 1995 по 2005 гг., и подумает — как же здорово, что я живу сейчас, а не в «застойных нулевых»! А поразмыслив еще немножко, добавит — о каком прорыве может идти речь, мы ведь уже достигли апогея? Впереди только медленная эволюция.
Но, как мы уже убедились чуть выше, в этом и заключается обманчивость экспоненциального роста. В реальности этот график должен говорить такому молодому человеку совсем другое. Его должно пугать то, что может случиться через очередные пару лет, так как вся мощность, достигнутая наукой за последние 100 лет, просто умножится на 2! И тот апогей, которым он восторгался, окажется лишь прямой линией на графике.
Ну и, конечно же, молодой человек из далеких «нулевых» думал точно так же, как и наш современник, глядя на тогдашний экспоненциальный график роста количества транзисторов на микросхеме:
Не буду тратить ваше время, но поверьте мне на слово, таким этот график был в любой период времени и каждый раз простые обыватели думали, что вот он — пик развития, а впереди лишь медленная эволюция.
Поэтому, когда я в своей заметке «Восстание машин» говорил о том, что в ближайшие 10-15 лет наш мир может измениться до неузнаваемости, я просто руководствовался здравым смыслом, зная о существовании логической ловушки под названием экспоненциальный рост.
Процессоры — не бактерии!
Но с чего, вдруг, я взял, что транзисторы должны уменьшаться по экспоненциальному росту? Это что, какой-то неизвестный миру «4-й закон Ньютона»?
Хорошее замечание! И на самом деле не существует никакого закона, которому бы могло подчиняться изменение размеров транзисторов. Мы не можем со стопроцентной уверенностью заявлять, что экспоненциальное развитие технологий продолжится. Но у нас есть десятки лет истории, из которой можно сделать 3 простых вывода:
А если это звучит неубедительно и вы понимаете английский, тогда рекомендую посмотреть интереснейшее интервью с Джимом Келлером — гениальным инженером и вице-президентом компании Intel. Похоже, нас ждут очередные 20 лет экспоненциального развития технологий.
Это значит, что современный взрывной рост (мощные смартфоны, голосовые ассистенты, дополненная реальность и вычислительная фотография) через 10 лет окажется всего лишь прямой линией на графике.
Кстати, не только количество транзисторов растет экспоненциально. В мире есть и множество других примеров. Население земли — один из них. Вдумайтесь только, тысячи лет истории привели к появлению первого миллиарда человек на планете. На второй миллиард ушло всего 100 лет. К отметке в 3 миллиарда мы подошли за 30 лет. А в последнее время население земли увеличивается на 1 миллиард каждые 10 лет.
Алексей, главный редактор Deep-Review
P.S. Не забудьте подписаться в Telegram на первый научно-популярный сайт о мобильных технологиях — Deep-Review, чтобы не пропустить очень интересные материалы, которые мы сейчас готовим!
Как бы вы оценили эту статью?
Нажмите на звездочку для оценки
Внизу страницы есть комментарии.
Напишите свое мнение там, чтобы его увидели все читатели!
Если Вы хотите только поставить оценку, укажите, что именно не так?