Что такое число тау
Математики хотят упразднить число Пи
Некоторые математики считают, что всем, начиная со школьников и заканчивая академиками, следует отказаться от использования при математических расчетах числа Пи. И вовсе не потому, что оно не точное, а из-за того, что им неудобно пользоваться. Гораздо выгоднее, с их точки зрения, использовать другую математическую константу — число Тау…
Что и говорить, математика — наука достаточно консервативная и степенная. Опровержение старых теорий,
которые достаточно часто случаются у
обходят эту отрасль человеческого знания стороной. Может быть, именно поэтому иногда математики начинают скучать и предлагать весьма оригинальные «реформы» своей дисциплины. Например, недавно группа ученых предложила упразднить известное всем со средней школы число… Пи.
Что предлагают изменить учёные, исключив число Пи из расчетов?
При этом «реформаторы» заявляют, что отменить эту математическую константу, выражающую отношение длины окружности к длине ее диаметра, следует вовсе не потому, что она «не справляется со своими обязанностями» (то есть не точна), а потому, что этим числом просто неудобно пользоваться. Но как же тогда вычислять длину окружности, спросите вы? Очень просто, ответят реформаторы. Вместо неудобного числа Пи следует использовать число Тау, которое выражает отношение длины окружности к ее радиусу. То есть, как вы понимаете, его значение в два раза больше числа Пи — если последнее приблизительно определяется как 3,14, то число Тау равно (тоже приблизительно) 6,28.
Что не нравится учёным в числе Пи?
За что же ученые мужи так взъелись на в общем-то не только безобидное, но и весьма полезное число Пи? Об этом может поведать один из самых непримиримых противников использования данной константы, бывший физик-теоретик, а ныне педагог Майкл Хартл из США:
«Несмотря на то, что прибегать к использованию числа Пи — путь ошибочный, непосредственно в самом определении этой постоянной никакой ошибки нет. Данная буква означает именно то, что вы хотите — так называемое отношение длины окружности к диаметру. Однако посудите сами — ведь окружность не диаметром задается, а радиусом. В соответствии со стандартным определением, окружностью называется фигура, которая состоит из всех точек плоскости, отнесенных от некоего центра на конкретную длину — то есть на радиус».
Итак, по мнению Хартла, вина числа Пи заключается всего лишь в том, что оно просто «неестественное». При этом ученый утверждает, что использование данной константы может сказаться на формировании сознания юных математиков.
«Когда вы начинаете задавать геометрическую постоянную круга посредством отношения длины окружности к ее диаметру, то это можно считать ни чем иным, как делением ее на удвоенный радиус, и данная двойка станет преследовать ваш ум в процессе всех вычислений», — предостерегает Хартл.
По мнению ученого, использование числа Тау избавит психику математика от этой самой «преследующей двойки» и сделает многие расчеты параметров окружности и круга
Кроме того, применение в расчетах именно этого числа таит в себе еще одну выгоду. Если измерять окружность не в градусах, а в радианах (радианом называется центральный угол, длина дуги которого равна радиусу окружности), то для того, чтобы выразить в данном случае полную окружность через Пи, нужно умножить радиус на два Пи, а при использовании числа Тау — потребуется умножить всего лишь на одно Тау.
Сначала (с 2001 года, когда профессор Университета Юты (США) Боб Пале опубликовал первую статью, в которой доказывал ошибочность применения числа Пи) данное предложение рассматривалось большинством математиков как некая блажь коллег из Западного полушария. Но со временем у него нашлось много сторонников и среди ученых Старого Света.
«Это одна из самых странных вещей, которые мне пришлось увидеть, но она имеет смысл. Удивительно, как люди раньше этого не поняли. Почти все, что мы делаем с числом Пи, мы можем делать и с числом Тау, но когда мы противопоставляем Пи и Тау, то Тау выигрывает — оно гораздо более натурально», — говорит британец Кевин Хьюстон, математик из Университета Лидса.
Итак, количество приверженцев числа Тау среди математиков неуклонно растет, хотя некоторые из них сомневаются в том, что его конкурента число Пи удастся так вот сразу упразднить. Ведь традиция использования данного числа имеет долгую историю.
Есть сведения, что этой константой пользовались еще
математики. Самое раннее из известных приближенных значений этого числа датируется 1900 годом до нашей эры. Причем вавилоняне определяли его как 25/8, а египтяне — как 256/8. Интересно, что оба значения отличаются от истинного не более, чем на один процент. А ведический текст «Шатапатха-брахмана» указывает значение Пи как 339/108 (приблизительно равно 3,139), что тоже довольно близко к истине.
Способ вычисления числа Пи: история появления
Первый же математический способ вычисления числа Пи предложил великий греческий математик и физик Архимед. Он был достаточно прост — ученый вписывал в окружность и описывал около нее правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. В итоге, рассматривая правильный 96-угольник, Архимед пришел к выводу, что число Пи должно вычисляться как среднее между значениями выражений 3+10/71 и 3+1/7. В итоге получилось, что искомое число равно 3,1419. Конечно, это не совсем точное значение, но все-таки весьма и весьма близкое.
Чуть позже, в 265 году нашей эры китайский математик Лю Хуэй из царства Вэй предложил свой алгоритм расчета числа Пи. Согласно ему, эта константа равна 3,14159. А в 480 году его коллега Цзу Чунчжи продемонстрировал, что Пи приблизительно равно 355/113, и показал, что Пи больше 3,1415926, но меньше 3,1415927. Любопытно, что данное значение этой константы считалось самым точным последующие 900 лет. Однако впоследствии ее значение неоднократно уточнялось.
Интересно еще и то, что в течение долгого времени эта важнейшая математическая константа была фактически безымянной. Впервые это число греческой буквой Пи обозначил британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. Согласно общепринятой версии, данное обозначение происходит от начальной буквы греческих слов περιφέρεια (окружность, периферия) и περίμετρος (периметр).
Так что, как видите, у числа Пи достаточно долгая и насыщенная история. Поэтому вряд ли его поклонники сдадутся без боя. Однако противники данной константы заявляют, что не собираются вытеснять Пи насильственными методами.
«Я не призываю к реальному насилию — ведь, согласитесь, это было бы уже дикостью, не так ли?» — заявляет самый непримиримый Пи-ненавистник Майкл Хартл.
Он даже выражает озабоченность по поводу того, что «…в процессе обращения в нашу веру многие люди становятся злы на Пи, чуть ли не как на своего личного врага. У них возникает ощущение, будто всю жизнь их обманывали, так что удивительно, какие гневные слова люди находят против этого числа — часто совсем уж неприличные».
Поэтому Хартл и его коллеги призывают к мирному вытеснению числа Пи из математической реальности и заменой его на число Тау. Они говорят, что следует постоянно пропагандировать абсурдность применения первого и удобство использования последнего. По их словам, людей нужно не заставлять отказываться от использования Пи, а убеждать в том, что Тау куда лучше. И тогда, по предположению Хартла, в конце концов число Пи тихо удалится из современной математики и займет свое место в архиве на полке «Математические константы прошлых веков».
Будет ли это так, или нет — сказать сложно. Как было сказано выше, математика — наука консервативная, и не было еще случая, чтобы кто-то из ее адептов отказался от использования традиционных констант. Но, может быть, число Пи станет первой из тех констант, которые сдали «в утиль» за ненадобностью…
Добавьте «Правду.Ру» в свои источники в Яндекс.Новости или News.Google, либо Яндекс.Дзен
Быстрые новости в Telegram-канале Правды.Ру. Не забудьте подписаться, чтоб быть в курсе событий.
Визуализация Пи, Тау и простых чисел

источник изображения
Возможно, вы видели предыдущий пост, где были предоставлены визуализации первых 1000 цифр и
. Он возник в результате небольшого спора о том, лучше ли
, чем
. По этому поводу идут бесконечные дебаты, и я подумал, что могу пошутить по этому поводу. В этом посте я хочу показать, как создать визуализации, и надеюсь, что вы захотите попробовать удивительный пакет Luxor.jl после прочтения. Вчера я начал читать туториал, и это потрясающе! В прошлый раз визуализация делалась на Javascript, и я подумал, что этот аккуратный маленький проект сойдет, чтобы начать изучать Луксор. Как уже упоминалось в let me be your mentor: я думаю, что очень важно иметь такие маленькие проекты, чтобы освоить новый инструмент.
Основная идея
Я хотел воссоздать визуализацию, которую видел в Numberphile от Мартина Крживинского.
Там был круг (который, вполне ассоциируется и с и с
) разделенный на 10 сегментов, по одному для каждой цифры. Цифры нашего иррационального числа представляются кривыми внутри этого круга, так что 3.1415 (я начинаю с 14) — это кривая от сегмента 1 до сегмента 4, а затем обратно к 1, потом до 5 и так далее. Каждый раз мы перемещаемся немного по часовой стрелке в сегменте так, что 1→4 создает различные кривые (в зависимости от текущего положения, в котором мы находимся).
Потом надобавляем всякие фичи. Мы должны начать чувствовать себя комфортно с Луксором. Важно: не надо искать математическую интерпретацию — это просто небольшой проект визуализации 😉
Я знаю, вам интересно, как должен выглядеть конечный результат:
Начинаем
вызываем vis() и создаем файл start.png который будет выглядеть как-то так:
Давайте быстренько пройдемся по командам:
просто хороший макрос. 🙂
Давайте сначала нарисуем внешний круг и добавим цифры:
Первая часть должна быть достаточно простой.
В настоящее время есть две проблемы:
Мы определяем следующую функцию, чтобы получить и соответствующую точку более простым способом:
Выглядит намного лучше! Давайте возьмем несколько хороших цветов из Colorschemes.jl.
помните, что индексация массивов в Julia начинается с единицы.
Каковы следующие шаги?
Я думаю, что визуально привлекательно иметь круг посередине, где мы можем добавить символ (или
) позже.
Поэтому мы не можем провести прямые линии от одного сегмента к другому. Для этого я использую квадратичные кривые Безье.
Давайте сначала получим цифры числа Пи:
Я должен уточнить, что я имею в виду под серединой: средняя точка между 0 и 4 должна быть 2, но между 8 и 0 она должна быть 9. Она определяется кратчайшим путем от одного сегмента к другому, а потом берется середина.
Кроме того, у меня на самом деле нет 10 дискретных сегментов, это просто для понимания. Я могу использовать среднюю точку 1,23 или что-то в этом роде. Это используется, потому что мы меняем нашу начальную и конечную позиции на основе текущей позиции, которую мы находимся в нашем массиве цифр.
Я надеюсь, что все станет яснее, ели взглянуть на код:
Давайте добавим еще несколько цифр и немного уменьшим ширину линии: setline(0.1)
Ладно я думаю что внутренний радиус немного велик:
Затем мы можем добавить в середине, прежде чем немного очистить код, чтобы создать нашу первую анимацию.
Luxor.jl не поддерживает латексные стринги LaTeXStrings.jl — это облом, но мы можем использовать UnicodeFun.jl.
и промеж циклов ставим:
Анимация
Я хотел бы получить gif из конвейера визуализации таким образом, чтобы в каждом кадре добавлялась новая линия.
У нас может быть сцена для устойчивого фона и одна для линий.
Прежде чем мы напишем функцию, давайте определим очень короткую анимацию, чтобы увидеть, как это делается.
Теперь я разделю все это дело на функции и определю переменные, такие как цифры, которые мы хотим визуализировать, чтобы нам было легче визуализировать или другие вещи.
Мы как бы потеряли возможность создавать простые образы. Поэтому я создал структуру
Тогда я могу использовать что-то вроде:
Не волнуйтесь, в конце есть репка, где вы можете увидеть весь код целиком. Просто немного сложно описать здесь изменения.
Может, мне стоило снять видео? 😀
Добавление точки Фейнмана
Мы визуализировали соединение цифр с цифрами с помощью кривых, но если бы у нас встретилось что-то вроде 555 в цифрах, мы бы видели только линию, идущую в направлении центра и обратно (или, может быть, мы видим две в зависимости от наших максимальных цифр, разрешения и т. д.)
Я только что проверил длину последовательности, и когда она больше 1, я рисую круг, где это происходит, и цвет — это цифра после этой последовательности. Большой круг в сегменте 9 — это так называемая точка Фейнмана, где цифра 9 появляется 6 раз в позиции 762.
Добавление гистограмм
Последняя вещь в моем списке — получить гистограмму на каждом сегменте, чтобы показать, случаются ли некоторые комбинации пар чаще, чем другие.
Для этого я использую функцию poly с четырьмя точками. В идеале, она должна быть ограничена двумя дугами, а не двумя линиями, но я оставляю это читателю 🙂
Да, можно было бы в принципе сгенерировать случайное число с 1000 цифрами и получить аналогичный результат.
Простое число
В двух словах: использование нашей функции для визуализации большинства элементов не так разумно, но так или иначе может получится что-то интересное.
При этом в качестве числовой последовательности используются последние цифры простых чисел. Я визуализировал простые числа меньше 100 000. Честно говоря, соединительные линии немного бесполезны, так как большую часть времени (если мы игнорируем первые несколько простых чисел: все время) возможны только четыре цифры. Это создает своего рода беспорядок в середине.
Тем не менее, гистограммы становятся все интереснее, я думаю:
Это ясно показывает, что не все пары одинаково вероятны. Особенно, если у нас есть простое число с последней цифрой x, то всегда менее вероятно, что последняя цифра
также заканчивается на x по сравнению с одним из трех других вариантов.
Давайте сосредоточимся на гистограммах и визуализируем простые числа под 10 000 000:
Я хотел бы создать что-то вроде штучек, из 3b1b.
По крайней мере, небольшие простые версии с некоторыми удобными функциями визуализации 🙂
Спасибо за чтение и особая благодарность моим 10 покровителям!
Я буду держать вас в курсе событий на Twitter OpenSourcES и на более личном:
Twitter Wikunia_de
Тау (2π)
Тау (τ) — математическая константа, выражающая соотношение длины окружности к радиусу.
Число тау равно 2π (примерно 6.283185…). Обозначается девятнадцатой буквой греческого алфавита «тау».
Свойства
Примечания
Полезное
Смотреть что такое «Тау (2π)» в других словарях:
ТАУ — теория автоматического управления ТАУ торфоаммиачные удобрения Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ТАУ телевизионное абонентное устройство ТАУ Толья … Словарь сокращений и аббревиатур
ТАУ — ТАУ (теория автоматического управления) это дисциплина, изучающая процессы автоматического управления объектами разной физической природы. ТАУ Тольяттинская академия управления. ТАУ Телевизионное агентство Урала … … Википедия
тау — алма. Тауда өсетін жабайы алма. Жаңа гүл жарған тобылғы мен т а у а л м а н ы ң исі мас қылғандай (Лен. жас, 10.06.1972, 2). Тау дерті. сөйл. Биіктік ауруы. Көш көсемі Зәйіп Тәйші дауа қонбас « т а у » д е р т і н е шалдығыпты (Егем. Қазақст., 15 … Қазақ тілінің түсіндірме сөздігі
тау — горный, буква Словарь русских синонимов. тау сущ., кол во синонимов: 2 • буква (103) • горный … Словарь синонимов
ТАУ — ТАУ, Таулы Гора, гористый; большой, высокий, подобный горе. Антрополексема. Татарские, тюркские, мусульманские мужские имена. Словарь терминов … Словарь личных имен
тау — I. 1. Җир өстенең һәр яктан текә биегәеп, күтәрелеп торган шактый зур урыны 2. күч. Һәрбер текәлек, битләү. с. Үрле, текә таурак урыннан менү 3. Бик зур булып өелгән өемнәр тур. кишерләрдән таулар өелде. ТАУ БАЛАВЫЗЫ – Җир өстенә чыгып куерган… … Татар теленең аңлатмалы сүзлеге
Тау’ри — Саманта Картер типичный представитель Тау ри Тау’ри (англ. Tau ri) Вид Тау’ри Родной мир Земля ( … Википедия
Тау — У этого термина существуют и другие значения, см. Тау (значения). Греческий алфавит Αα Альфа … Википедия
Тау — (Евр.) То, что теперь стало еврейской квадратной буквой тау, но задолго до изобретения еврейского алфавита являлось египетским крестом с рукояткой, крукс ансата римских народов, и идентично с египетским анкх. Этот знак принадлежал и теперь… … Религиозные термины
ТАУ — (Евр.) То, что теперь стало еврейской квадратной буквой тау, но задолго до изобретения еврейского алфавита являлось египетским крестом с рукояткой, крукс ансата римских народов, и идентично с египетским анкх. Этот знак принадлежал и теперь… … Теософский словарь
Манифест тау
Майкл Хартл
День тау, 2010
обновлено на день тау 2020
1 Константа окружности
Манифест тау посвящён одному из самых важных, возможно самому важному числу в математике: константе окружности, связывающей длину окружности с её линейным измерением. Тысячами лет окружность считалась самой идеальной геометрической фигурой, и в константе окружности содержится вся геометрия окружности, в едином числе. Конечно, традиционный выбор для константы окружности это \( \pi \) (пи) — но, как математик Боб Палэй замечает в своей восхитительной статье “ \( \pi \) Is Wrong!”, 1 \( \pi \) неправильное число. Наступило время всё исправить.
1.1 Нескромное предложение
У этого числа \( \pi \) есть много замечательных свойств — среди других, оно иррационально и, конечно, трансцендентно — и оно присутствует в огромном количестве математических формул.
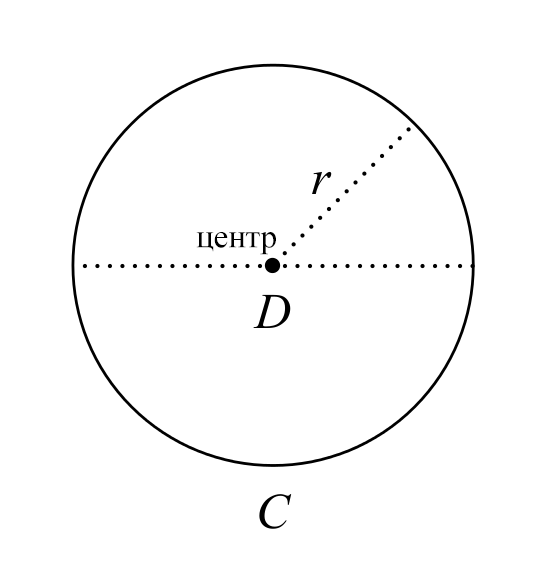
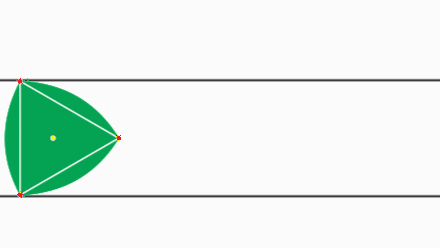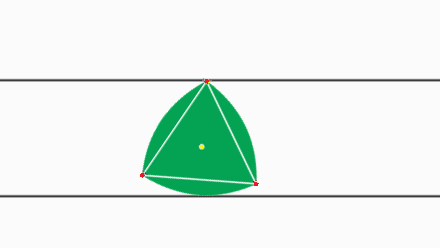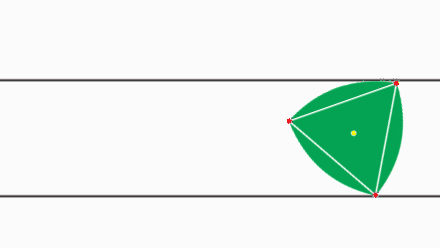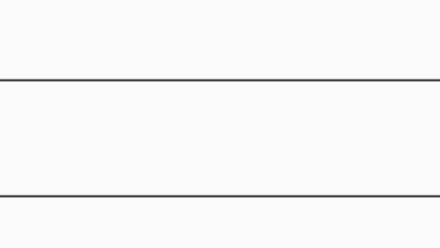
Должно быть очевидным, что \( \pi \) не «неправильно» в том смысле, что его значение неточное; значение числа \( \pi \) точное, и у него есть все свойства, которые ему приписывают математики. Когда мы говорим, что “ \( \pi \) неправильное число”, мы имеем ввиду то, что \( \pi \) запутанный и неестественный выбор для константы окружности. В частности, окружность определена как множество точек, удалённых на одно и то же расстояние, радиус, от заданной точки, центра окружности (Картинка 1 ). В то время как существует бесконечное количество геометрических фигур с постоянной шириной, (Картинка 2 ), 3 существует только одна фигура с постоянным радиусом. Это намекает на то, что более естественное определение для константы окружности должно использовать \( r \) вместо \( D \) :
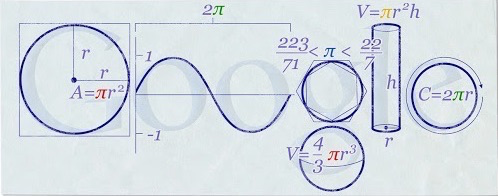
В статье “ \( \pi \) Is Wrong!”, Боб Палэй приводит веские доводы в пользу второго из этих двух определений для константы окружности, и по моему мнению заслуживает статус первого человека, который указал на это большой аудитории. Он называет истинную константу окружности «один поворот», и он также создаёт новый символ для этого числа (Картинка 3 ). Как мы позже увидим, определение этого числа верно, но к сожалению символ довольно странен, и (как обсуждается в Разделе 4 ), скорее всего он не будет широко использоваться.
Манифест тау посвящён утверждению, что правильный ответ на “ \( \pi \) неправильное число” это “да, на самом деле.” И истинная константа окружности заслуживает соответствующее имя. Как можно было уже догадаться, манифест тау предлагает, чтобы этим именем была греческая буква \( \tau \) (тау):
В течение этой статьи мы убедимся, что число \( \tau \) это правильный выбор, и мы покажем с помощью конкретных примеров использования (Раздел 2 and Раздел 3 ) и приведением прямых доводов (Раздел 4 ), что буква \( \tau \) также является естественным выбором.
1.2 Сильный враг
В то же время, некоторые люди запоминают дюжины, сотни, даже тысячи цифр этого мистического числа. Какой несчастный человек запоминает даже 40 цифр \( \pi \) (Картинка 5 )? 4
Воистину, сторонники \( \tau \) стоят перед мощным оппонентом. И всё же, на нашей стороне стоит мощный сторонник — истина.
2 Число тау
и в значениях дзета-функции Римана для положительных чётных чисел: 5
Эти формулы не были выбраны специально — откройте свой любимый учебник по физике или математике и убедитесь сами. Есть ещё очень много примеров этого, и вывод ясен: в величине \( 2\pi \) есть что-то особенное.
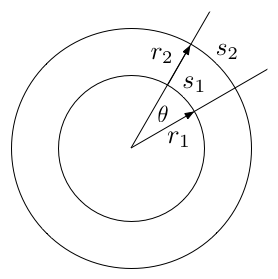
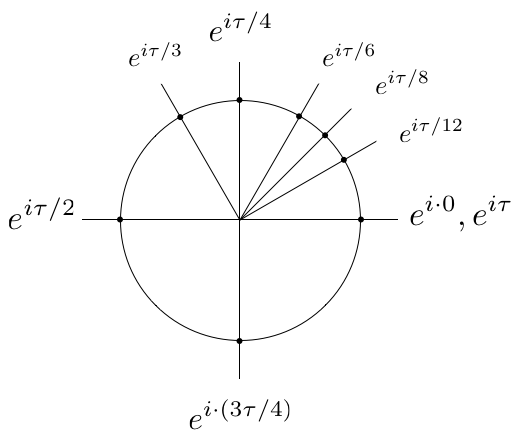
2.1 Окружности и углы
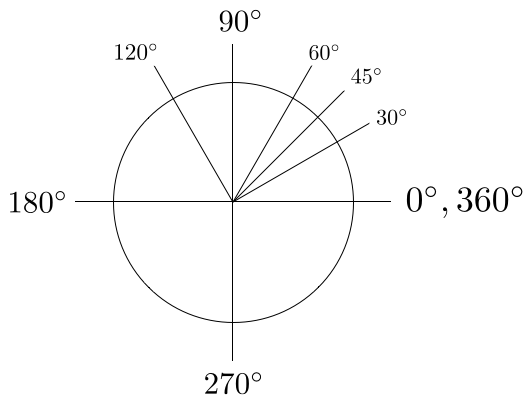
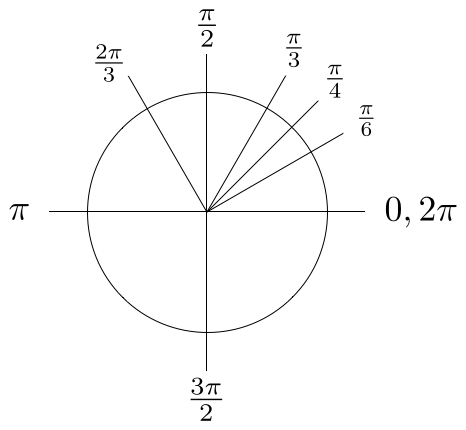
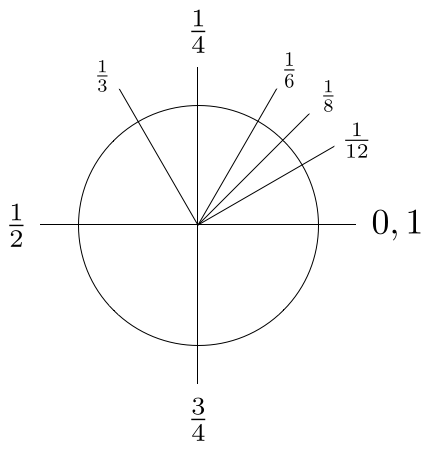
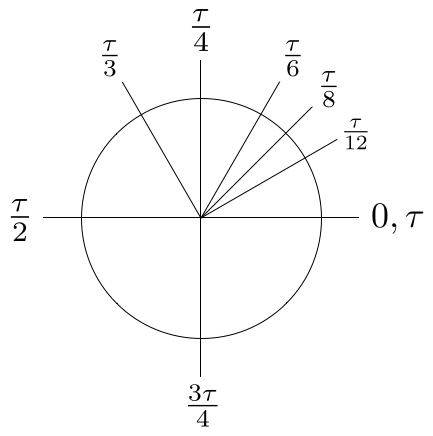
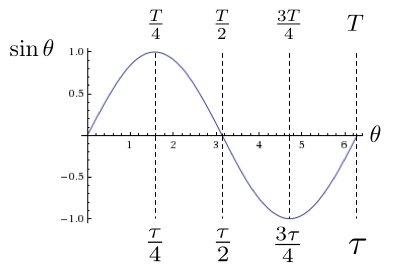
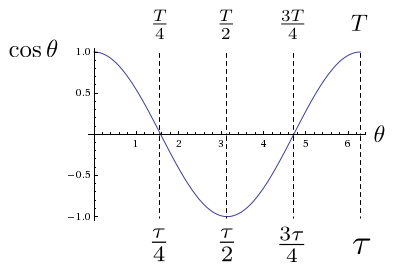
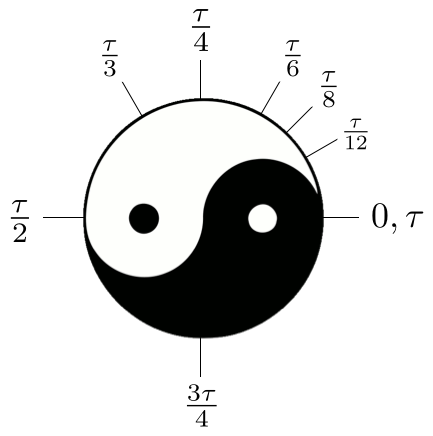
Возможно, самая простая система углов это градусы, где окружность делится на 360 равных частей. Ученикам, изучающим тригонометрию, в этой системе говорят запоминать особые углы, показанные на Картинке 7.
Это даёт следующее определение величины угла в радианах:
Отступление
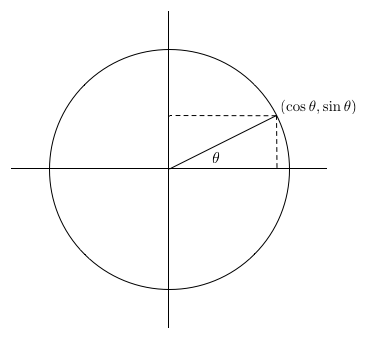
2.2 Функции окружности
Именно. Я был удивлён обнаружить, что я уже забыл что \( \tau/2 \) иногда называется “ \( \pi \) ”. Возможно, то же самое случилось с вами сейчас. Добро пожаловать в мой мир.
2.3 Тождество Эйлера
Меня нельзя было бы простить, если в этом манифесте не было написано про тождество Эйлера, иногда называемое “самым красивым уравнением в математике”. Это тождество связано с комплексным возведением в степень, которое в свою очередь глубоко связано как и с функциями окружности, так и с самой геометрией окружности.
В зависимости от того, какой путь выбран, следующее уравнение может быть или доказано, или взято как определение; в любом случае, оно довольно замечательное:
Определение значения Ур. ( 5 ) при \( \theta = \tau \) приводит к тождеству Эйлера: 7
В словах, Ур. ( 5 ) делает следующее фундаментальное наблюдение:
Комплексный экспоненциал константы окружности равен единице.
Геометрически, умножение на \( e^
Поворот на один оборот это 1.
Как и в случае с радианами, мы видим естественную ассоциацию между \( \tau \) и одним оборотом вокруг окружности. Безусловно, приравнивание \( \tau \) с “одним оборотом” делает тождество Эйлера почти тавтологией. 8
Не самое красивое уравнение
Но этот знак минуса настолько уродлив, что Ур. ( 7 ) почти всегда сразу перестанавливают, давая тем самым следующее «красивое» уравнение:
В этом контексте удивительно то, сколько людей жалуются, что Ур. ( 6 ) связывает между собой только четыре из этих пяти чисел. Ладно:
Тождества Эйлера
Нет, погодите. Формула для площади всегда пишется используя радиус, вот так:
3.1 Квадратичные формы
Падение в однородном гравитационном поле
Галилео Галилей обнаружил, что скорость тела, падающего в однородном гравитационном поле пропорциональна времени падения:
Константа пропорциональности — ускорение свободного падения \( g \) :
Так как скорость это производная положения, мы можем расчитать расстояние, которое прошло тело в падении с помощью интегрирования:
Потенциальная энергия в пружине
Роберт Гук обнаружил, что внешняя сила, необходимая для того, чтобы растянуть пружину, пропорциональна расстоянию, на которое пружина была растянута:
Константа пропорциональности — коэффициент упругости \( k \) : 9
Потенциальная энергия в пружине тогда равна работе, совершённой внешней силой:
Энергия движения
Исаак Ньютон обнаружил, что сила, приложенная к телу пропорциональна его ускорению:
Константа пропорциональности — масса \( m \) :
Энергия движения, или кинетическая энергия, равна механической работе, совершённой при ускорении массы до скорости \( v \) :
3.2 Предчувствие дурного
Увидев несколько примеров квадратичных форм в физике, у вас сейчас возможно появилось предчувствие дурного при нашем возвращении к геометрии окружности. Это ощущение оправдано.
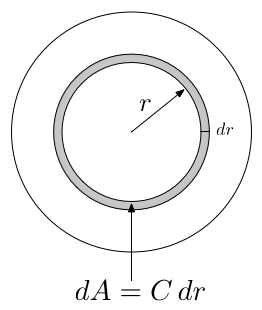
Теперь, длина окружности пропорциональна её радиусу:
Константа пропорциональности это \( \tau \) :
Площадь окружности, тогда, это интеграл по всем кольцам:
Этот множитель одной второй невозможно оставить позади (Таблица 3 ).
| Величина | Символ | Формула |
| Расстояние, на которое упало тело | \( y \) | \( \textstyle<\frac<1><2>>gt^2 \) |
| Энергия пружины | \( U \) | \( \textstyle<\frac<1><2>>kx^2 \) |
| Кинетическая энергия | \( K \) | \( \textstyle<\frac<1><2>>mv^2 \) |
| Площадь окружности | \( A \) | \( \textstyle<\frac<1><2>>\tau\,r^2 \) |
Quod erat demonstrandum
4 Конфликт и сопротивление
4.1 Один оборот
Есть две главные причины использовать \( \tau \) для константы окружности. Первая заключается в том, что \( \tau \) внешне напоминает \( \pi \) : после столетий использования, ассоциация \( \pi \) с константой окружности неизбежна, и использование \( \tau \) получает пользу от этой ассоциации, вместо борьбы с ней. (Конечно, горизонтальная линия в каждой букве намекает на ассоциацию «ног» со знаменателями, так что у \( \pi \) две ноги в его знаменателе, в то время как у \( \tau \) только одна. С этой точки зрения, отношение \( \tau = 2\pi \) абсолютно естественно.) 10
После изначального запуска манифеста тау, я узнал, что Питер Хэрримоэс независимо предложил использовать \( \tau \) автору статьи “ \( \pi \) Is Wrong!” Бобу Палэю в 2010, Джон Фишер предложил \( \tau \) посте на Usenet в 2004, и Джозеф Линдерберг предвидел как довод, так и символ более чем 20 лет до этого! 11 Доктор Хэрримоэс, в частности, акцентировал внимание на доводе, сделанный в Разделе 1.1 : использование \( \tau \) даёт константе окружнорсти имя. Так как \( \tau \) это обыкновенная буква греческого алфавита, люди, встречающие её в первый раз, сразу смогут её произнести.
Двусмысленная система обозначений
Вместо создания нового символа, в манифесте тау предлагается использование уже существующей греческой буквы. Как следствие, так как \( \tau \) уже используется в некоторых существующих контекстах, мы должны поговорить о потенциальном конфликте с существующей практикой. К счастью, наш символ довольно редко используется часто. Более того, в то время как \( \tau \) используется для некоторых конкретных переменных — например, напряжения сдвига в машиностроении, момента силы в механике, и собственного времени в особой и общей теориях относительности — не существует всеобщего противоречащего использования. 13 В этих случаях, мы можем игнорировать двусмысленность или обойти проблему стороной, выборочно поменяв уже используемые символы. Например, можно использовать \( N \) для момента силы 14 или \( \tau_p \) для собственного времени.
Один пример легко переносимой двусмысленности происходит в квантовой механике, где мы встречаем следующую формулу для радиуса Бора, которая (грубо говоря) является «размером» атома водорода в его самом низком энергетическом уровне (основном уровне):
где \( m \) это масса электрона и \( e \) его заряд. В то же самое время, сам основной уровень описывается величиной, известной как волновая функция, которая падает экспоненциально с радиусом на масштабах длины, заданных радиусом Бора:
где \( N \) это нормирующая постоянная.
Уже заметили проблему? Скорее всего нет, в этом и суть. «Проблема» заключается в том, что \( e \) в радиусе Бора и \( e \) в волновой функции не одна и та же \( e \) — первая это заряд электрона, в то время как вторая это основание натурального логарифма. Более того, если мы подставим под \( a_0 \) его значение в Ур. ( 10 ), мы получим
С первого взгляда, похоже на то, что это более естественно, чем версия с \( \tau \) :
Как всегда, внешность обманчива: значение \( N \) задаётся произведением
4.2 Манифест пи
Хотя и большинство аргументов против \( \tau \) приходят через случайную переписку по электронной почте и различными комментариями в интернете, есть и организованная оппозиция. В частности, с начала публикации манифеста тау в июне 2010, “Pi Manifesto” («манифест пи») появился, чтобы привести доводы в пользу традиционной константы окружности. Этот раздел, и два разделе после него содержат опровержение этих аргументов. Неизбежно то, что контраргументы будут немногословны и технически более сложные, чем остальная часть этого манифеста, но даже если не сильно вдаваться в подробности того, что будет написано далее, даст вам достаточно информации, чтобы понять, что аргументы, приведённые в манифесте пи слабы.
В то время, как мы можем определённо считать появление манифеста пи хорошим знаком продолжающегося интереса в этой теме, манифест делает несколько ложных утверждений. Например, в нём говорится, что множитель \( 2\pi \) в гауссовском (нормальном) распределении это совпадение, и то, что оно может быть более естественно записано как
Связанное с этим утверждение это то, что Гамма-функция в точке \( 1/2 \) записывается в более естественной форме с помощью \( \pi \) :
5 Тщательное изучение пи и тау
Заметка: Этот раздел сложнее, чем остальная часть манифеста, и может быть пропущен без потери непрерывности данного манифеста. Если вы найдёте этот раздел запутанным, я рекомендую сразу перейти в заключению в Разделе 6.
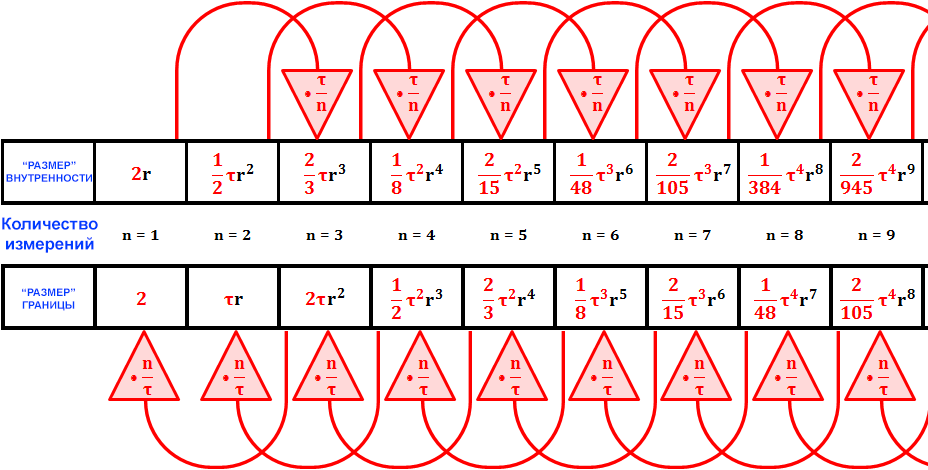
5.1 Площадь поверхности и объём гиперсферы
Её внутренность, которая удовлетворяет
где гамма-функция задана Ур. ( 11 ). Ур. ( 14 ) это частный случай формулы с радиусом, который обычно записывается, используя \( \pi \) :
С этой точки зрения, \( \Gamma \) может быть интерпретирована как обобщение функции факториала для вещественных аргументов. 19
Интегрирование по \( r \) даёт
Чтобы разгадать эту загадку, мы начнём с более тщательного изучения формулы для нечётных \( n \) в Ур. ( 18 ):
После того, как мы исследуем выражение
мы заметим, что его можно перезаписать как
Теперь, давайте взглянем на чётный случай в Ур. ( 18 ). Мы заметили сверху странность, использование обыкновенного факториала для чётного случая и двойного факториала для нечётного случая. Конечно, потому что двойной факториал уже определён частями, если мы объединим формулы используя \( n!! \) в обоих случаях, мы сможем вытащить его как общий множитель:
Так есть ли какая-либо связь между факториалом и двойным факториалом? Да — когда \( n \) чётное, обе функции связаны следующим уравнением:
(В этом легко убедиться с помощью математической индукции.) Подставляя это в формулу объёма для чётных \( n \) даёт нам
что очень сильно похоже на
Объединив эти результаты воедино, мы видим, что Ур. ( 18 ) может быть перезаписано как
и Ур. (17) может быть перезаписано как
Делая подстановку \( \tau=2\pi \) в Ур. ( 21 ) даёт нам
что позволяет нам записать формулу следующим образом:
Интегрирование Ур. ( 22 ) по \( r \) даёт нам
Лямбда
где множитель \( 2^2 \) появляется из-за \( 2^2 \) конгруэнтных дуг окружности (по одной из каждой четверти) в двумерном пространстве.
Это означает, что мы можем переписать произведение
что убирает явную зависимость от чётности. Применяя Ур. ( 26 ) к Ур. ( 22 ) и Ур. ( 23 ) даёт нам
Рекуррентные формулы
Похожим образом, для площади поверхности мы имеем
таким образом показывая, что приравнивание \( \tau \) к «константе рекуррентных отношений» не совпадение — константа рекуррентных отношений и константа окружности на самом деле одно и то же:
5.2 Три семьи констант
С двумя семьями констант, определённых в Ур. ( 32 ) and Ур. ( 33 ), мы можем записать формулы площади поверхности и объёма (Ур. ( 27 ) и Ур. ( 28 )) компактно следующим образом:
Таким образом, мы видим, что \( \pi \) естественным образом ассоциирован с площадями поверхностей, поделёнными на степень диаметра, необходимую чтобы получить безразмерную константу. Это приводит к созданию третьей семьи констант \( \pi_n \) :
Мы можем выразить это через семью \( \tau_n \) подставив \( D = 2r \) в Ур. ( 34 ) и применив Ур. ( 32 ):
Это на самом деле равно \( \pi_2 \) :
Но это равенство совпадение: оно происходит только потому что \( 2^
6 Заключение
6.1 Часто Задаваемые Вопросы
Вся «проблема» заключается в этой механической подстановке, полностью ясной и конечно же полностью обратимой. Переключение с \( \pi \) на \( \tau \) может случится медленно. В отличии от переопределения, всё не происходит в один момент.
6.2 Прими тау
Мы увидели в манифесте тау, что естественный выбор для константы окружности это отношение длины окружности не к её диаметру, а к её радиусу. Этому числу нужно название, и я надеюсь что вы присоединитесь ко мне, и будете называть её \( \tau \) :
6.3 День тау
Share the τ Manifesto
Thanks! Now check your email and click on the confirmation link.
Благодарности
Сначала я хотел бы поблагодарить Боба Палэя за написание статьи “ \( \pi \) Is Wrong!”. Я не помню, насколько глубоки были мои подозрения касательно \( \pi \) перед тем как я прочёл эту статью, но “ \( \pi \) Is Wrong!” определённо открыла мне глаза, и каждый раздел манифеста тау это моя благодарность Бобу. Я бы также хотел поблагодарить его за полезные комментарии на тему этого манифеста.
Я думал о манифесте тау достаточно долго, и многие идеи, представленные здесь были разработаны с помощью общения с моим другом Сумитом Дафтуаром. Его идеи как учителя и математика повлияли на моё мышление различными образами.
В конце концов, я бы хотел поблагодарить Уаятта Грина за его необычайный полезный фидбэк на версию манифеста перед запуском; помимо других вещей, если вам нужен кто-то, кто скажет, что «почти весь [ныне убранный] раздел 5 полное дерьмо», Уаятт готов помочь.
Об авторе
Копирайт
Манифест тау. Копирайт © 2010–2018, автор Майкл Хартл. Электронные версии манифеста тау доступны для приобретения через сайт продаж манифеста тау. Пожалуйста, не стесняйтесь печатать и распространять копии манифеста тау для школьных или схожих использований.
Buy Print Edition
Get the print edition of The Tau Manifesto at Amazon!
Get your own Tau Tee
Celebrate Tau Day in style with a Tau T-shirt from Teespring!
Thanks! Now check your email and click on the confirmation link.