Что такое частота в эксель
Функция ЧАСТОТА
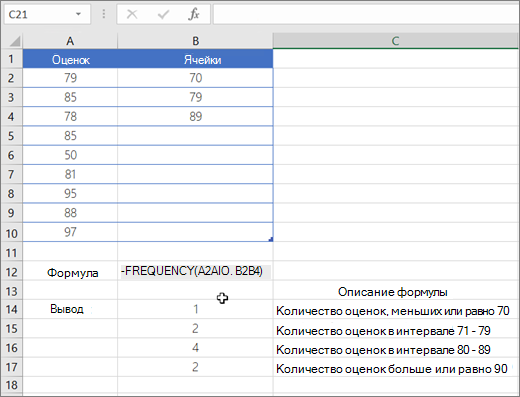
Функция ЧАСТОТА вычисляет частоту ветвей значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
Аргументы функции ЧАСТОТА описаны ниже.
data_array — обязательный аргумент. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
bins_array — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Пример
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
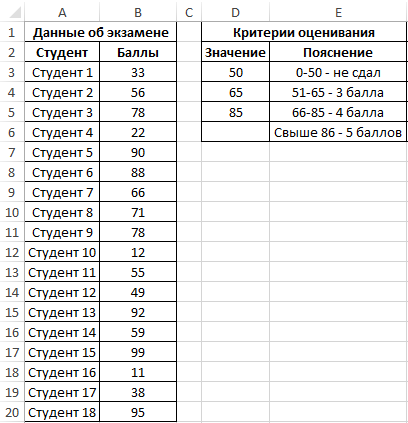
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
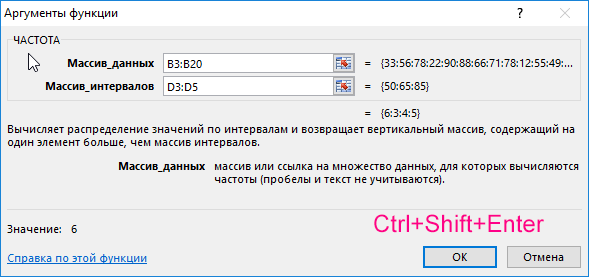
Для решения выделим области из 4 ячеек и введем следующую функцию:
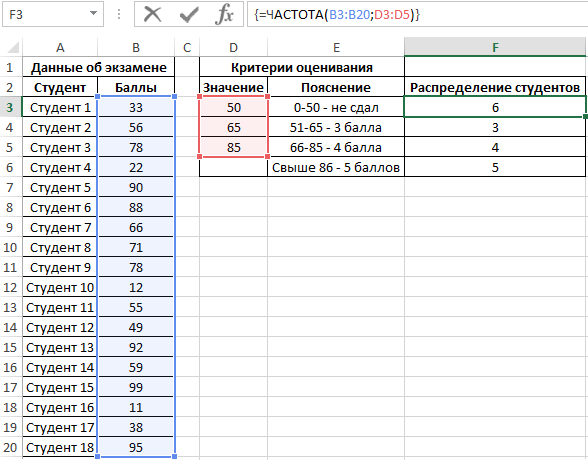
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки <> в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
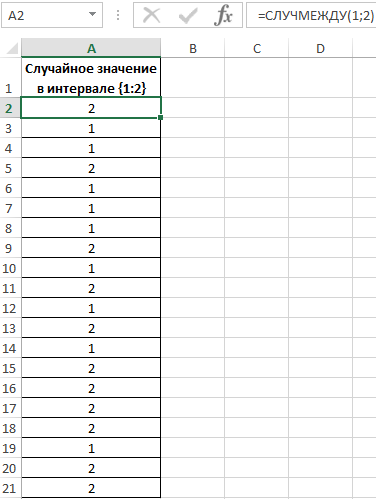
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
Для определения случайных значений в исходной таблице была использована специальная функция:
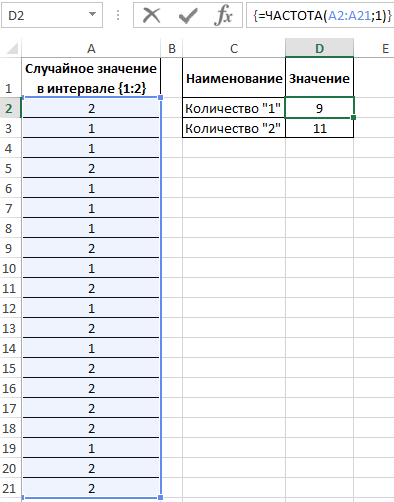
Для определения количества сгенерированных 1 и 2 используем функцию:
В результате получим:
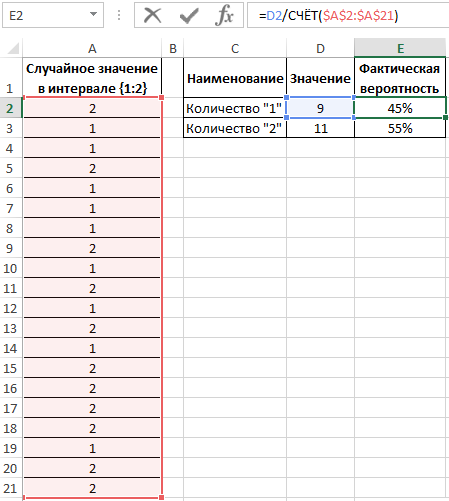
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
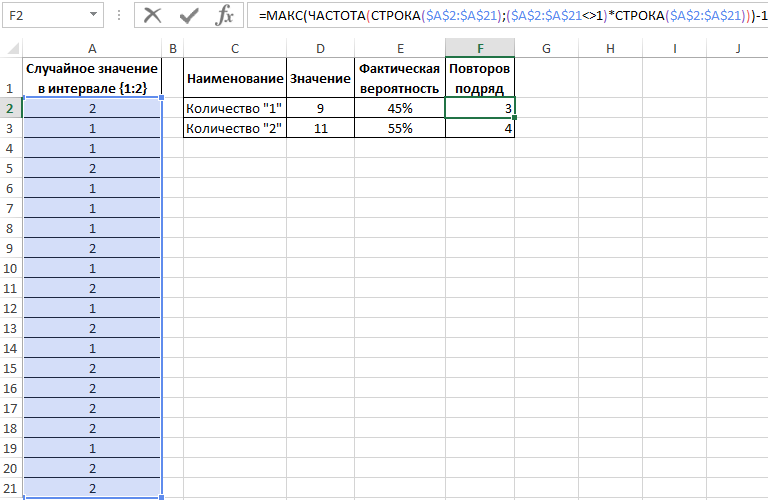
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
1)*СТРОКА($A$2:$A$21)))-1′ >
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
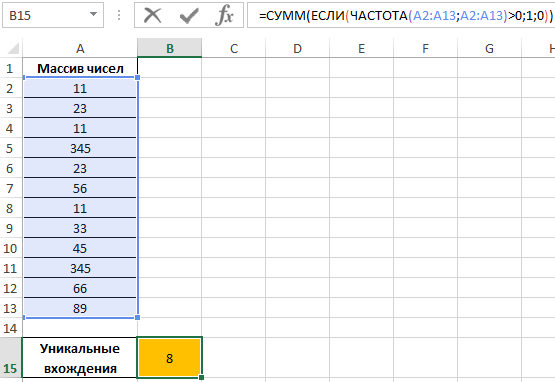
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
Полученное значение (количество единиц) суммируется.
В результате получим:
То есть, в указанном массиве содержится 8 уникальных значений.
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
ЧАСТОТА Функция Excel
Функция ЧАСТОТА в Excel
Функция ЧАСТОТА в Excel вычисляет, сколько раз значения данных встречаются в заданном диапазоне значений. Он возвращает вертикальный массив чисел, соответствующий частоте каждого значения в диапазоне. Это встроенная функция Excel, относящаяся к категории статистических функций.
Формула ЧАСТОТЫ в Excel
Ниже представлена формула ЧАСТОТЫ в Excel.
Аргументы, используемые для формулы ЧАСТОТА в Excel.
Объяснение функции ЧАСТОТА в Excel
Частота возвращает массив значений, и поэтому ее необходимо ввести как формулу массива, то есть нажать CTRL + Shift + Enter (или Command + Shift + Enter для Mac). Ячейки, в которые требуется вывод, эти ячейки должны быть выбраны в первую очередь, а затем вводится формула ЧАСТОТА в excel, после чего она вводится как формула массива.
Выберите ячейки à Введите формулу à Нажмите CTRL + Shift + Enter.
Возврат
ЧАСТОТА Функция в Excel возвращает частотное распределение data_array в bins_array интервалы. Результат всегда на единицу больше, чем количество элементов в bins_array. Дополнительный элемент в возвращаемом массиве соответствует количеству значений, превышающих самый высокий элемент bins_array. Предположим, что bins_array содержит три элемента <2, 4, 6>, функция вернет четыре элемента < 6>.
Если данные_массив не содержит значений, функция ЧАСТОТА Excel возвращает массив нулей. Если bins_array не содержит значений, функция ЧАСТОТА Excel возвращает общее количество элементов, указанных в data_array.
ЧАСТОТА в Excel — широко используемая функция в статистике. Иногда требуется понять частотное распределение заданных данных, а не только данных. Например, возраст людей в популяции сильно различается и поэтому отображается в виде частот. Точно так же оценки, полученные каждым учеником в классе, объединяются по частотам, чтобы понять общую успеваемость класса.
ЧАСТОТА в Excel — Иллюстрация
Предположим, у вас есть числа, для которых вы хотите рассчитать частоту. Цифры <1, 3, 2, 4, 6, 2, 3, 4, 5>приведены в B3: B11.
Номера должны быть разбиты на интервалы: <2, 4, 6>, указанные в D3: D5.
Чтобы вычислить частоту, сначала выберите четыре ячейки E3: E6, а затем следующий синтаксис:
= ЧАСТОТА (B3: B11; D3: B5)
и нажмите CTRL + Shift + Enter.
Поскольку количество возвращаемых элементов на единицу больше, чем количество элементов в bins_array, в этом случае вам нужно выделить четыре ячейки.
Данный выход <3, 4, 2, 0>соответствует интервалу < 6>.
Если вы выберете только три ячейки вместо четырех, счет «больше 6» будет опущен, как показано ниже.
Как использовать функцию ЧАСТОТА в Excel?
Функция ЧАСТОТА в Excel очень проста и удобна в использовании. Давайте разберемся с работой FREQUENCY in excel на некоторых примерах.
Пример # 1
Предположим, вы провели опрос и собрали данные о росте, как показано ниже.
Теперь вы хотите рассчитать частоту роста в следующих интервалах:
Интервалы <155, 160, 165, 170>приведены в E4: E7.
Чтобы вычислить частоту, сначала выберите пять последовательных ячеек (4 + 1).
Затем введите следующий синтаксис:
= ЧАСТОТА (B4: B14; E4: E7)
и нажмите CTRL + Shift + Enter.
Пример # 2
Предположим, у вас есть список удостоверений учащихся, не сдавших экзамен по одному или другим предметам в вашем классе, а также предметы, как показано ниже.
Теперь все те, кто потерпел неудачу (по одному или нескольким предметам), будут считаться «провалившимися». Теперь вам нужно знать количество студентов, которые проиграли.
Чтобы определить это, вы можете использовать следующий синтаксис:
= СУММ (- (ЧАСТОТА (B4: B9; B4: B9)> 0))
Давайте подробно рассмотрим синтаксис:
ЧАСТОТА (B4: B9, B4: B9) вычислит частоту данных B4: B9 с использованием интервала B4: B9. Он вернет
FREQUENCY (B4: B9, B4: B9)> 0 проверяет, больше ли полученная частота нуля. Он возвращает логическое ИСТИНА, если оно больше нуля, иначе ЛОЖЬ. Он вернет
SUM (- (FREQUENCY (..)> 0)) затем суммирует ИСТИНА и возвращает количество уникальных значений.
Пример # 3
Предположим, у вас есть данные о клиентах, посещенных в супермаркете за день, а также время их посещения в ячейках B4: C20, как показано ниже.
Теперь вы хотите узнать, в какие промежутки времени покупатели чаще всего посещали магазин. Это поможет вам эффективно спланировать рабочее время сотрудников. Магазин открывается в 11:00 и закрывается в 20:00.
Давайте сначала определимся с временным интервалом. Мы можем использовать следующие интервалы для простоты:
Теперь выберите ячейки в частотной таблице, чтобы получить. G4: в данном случае G13. Поскольку магазин закрывается в 20:00, мы не выбираем ячейку для> 20:00, так как во всех случаях она будет равна нулю.
Теперь введите следующий синтаксис:
= ЧАСТОТА (B4: C39, G4: G13)
и нажмите CTRL + Shift + Enter.
Он вернет частоту посещения магазина покупателем. В этом случае большинство посещений приходилось на период с 17:00 до 18:00.
Формула частоты Excel
Формула частоты Excel (Содержание)
Формула частоты в Excel
Формула частоты в Excel вычисляет или определяет распределение частоты набора данных, т. Е. Сколько раз это значение появляется в пределах диапазона значений.
Определение формулы частоты в Excel
Синтаксис для формулы частоты в Microsoft Excel:
Формула частоты в Excel имеет два аргумента, которые приведены ниже:
Формула частоты должна быть введена как формула массива для нескольких частот или, если мы хотим найти несколько бинов или вернуть несколько значений частоты, она должна быть введена как формула массива с опцией CTRL + SHIFT + ENTER в Excel.
Как использовать формулу частоты в Excel?
Частота Формула в Excel очень проста и удобна в использовании. Давайте разберемся в работе формулы частоты в Excel на нескольких примерах.
В приведенном ниже примере таблица содержит различное количество объектов возрастной группы. Мне нужно выяснить частоту возрастной группы до или равной 10 годам. Здесь формула частоты подсчитывает, как часто значения встречаются в диапазоне или массиве в Excel.
Таким образом, результат будет таким, как указано ниже.
В приведенном выше расчете единой частоты вы можете заметить, что в формуле частоты Excel найдено 2 значения или члена, где их возраст меньше или равен 10 годам. (Возраст> или = 10 лет)
В приведенном ниже примере таблица содержит члена с различными возрастными сущностями. Мне нужно выяснить или рассчитать распределение частот среди разных возрастных групп 17 человек в возрасте от 9 до 80 лет.
Как мы хотим узнать несколько значений частоты здесь. Мне нужно выяснить распределение частот четырех разных возрастных групп здесь, поэтому нам нужно ввести значения массива четырех ячеек, чтобы были выбраны значения или диапазон четырех ячеек, то есть D2: D5. Нажмите ОК, после ввода двух аргументов. ЧАСТОТЫ (А2: А18, D2: D5)
Примечание. Разные возрастные группы делятся на 4 возрастные группы, так что это будет четыре значения bins_array.
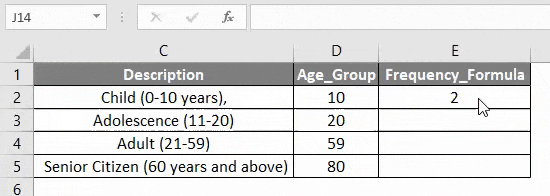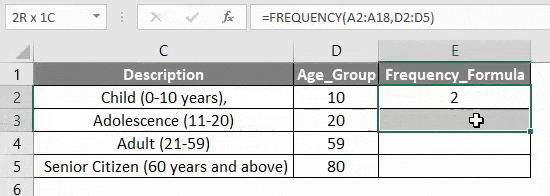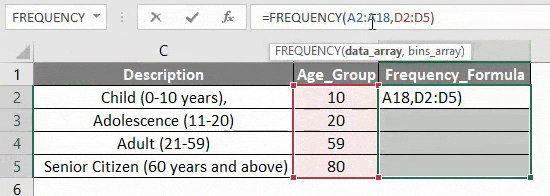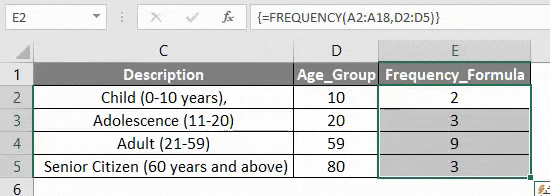
Результат будет таким, как указано ниже.
Теперь вы можете заметить, что значение имеет только первая ячейка столбца Frequency, остальные ячейки пустые.
Чтобы получить другие значения, выберите диапазон ячеек от E2 до E5. Как только он выбран, щелкните внутри набора данных панели формулы частоты. Теперь вы можете видеть, что все три диапазона значений выделены тремя разными цветами, теперь нажмите CTRL + SHIFT + ENTER, чтобы применить формулу массива.
Теперь вы можете увидеть столбец результатов частоты, он отображает все пропущенные значения.
На панели инструментов формул вы можете увидеть фигурные скобки для формулы массива
Что нужно помнить о формуле частоты в Excel
Рекомендуемые статьи
Функция частота в excel примеры
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА(массив_данных;массив_интервалов)
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
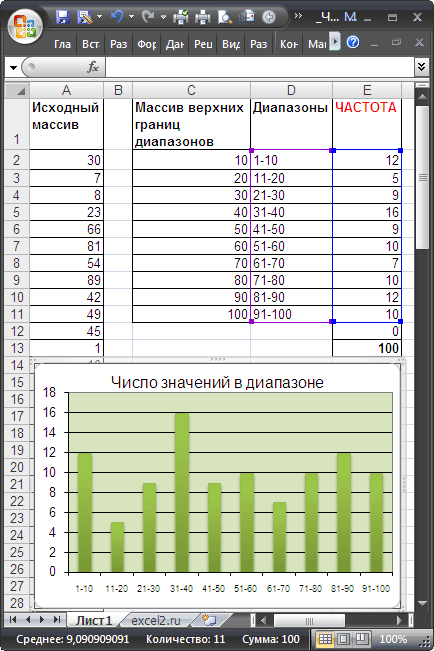
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
Примечание. Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
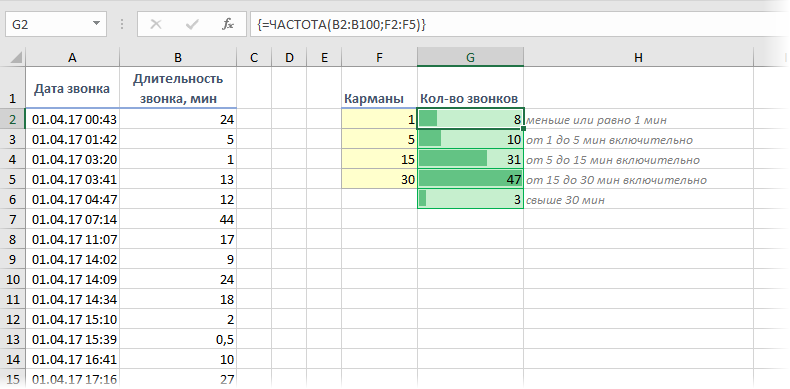
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
=ЧАСТОТА( Данные ; Карманы )
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
Для решения выделим области из 4 ячеек и введем следующую функцию:
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки <> в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
Для определения случайных значений в исходной таблице была использована специальная функция:
Для определения количества сгенерированных 1 и 2 используем функцию:
В результате получим:
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» – 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
1)*СТРОКА($A$2:$A$21)))-1′ >
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
Полученное значение (количество единиц) суммируется.
В результате получим:
То есть, в указанном массиве содержится 8 уникальных значений.
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.