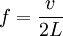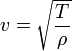Что такое частота резонанса
Про резонансную частоту, часть 1
Попробуем разобраться с ключевыми параметрами динамиков. Начнем с одного из самых основных параметров — с резонансной частоты(fs). Писал очень долго и муторно, сотни раз переделывал и переписывал, и получилось многабукафф:) Поэтому разбил на две части. Во второй части будет о том, как фс ведет себя при различных оформлениях и резонанс применительно к высокочастотникам.
От вас жду дополнений и исправлений! Попробуем вместе создать действительно хорошие тексты, доступно разъясняющие основы и физику звука. Надеюсь, не только мне хочется от и до во всем разобраться:) Текст не самый легкий, поэтому включаем думалку, и вперед:) Поехали!
Итак, резонансная частота. Разумеется, этот параметр не самодостаточный и для построения сколь угодно качественной системы знания одного его будет мало.
Динамик, как и любая колебательная система, имеет свою резонансную частоту. Это не незыблемая величина, она может довольно сильно меняться в зависимости от разных факторов. Например, температура упала => подвесы задубели – резонанс возрос. Закинули динамик в ЗЯ – резонанс возрос. Накидали на колпак сортирки с ПВА – резонанс упал.
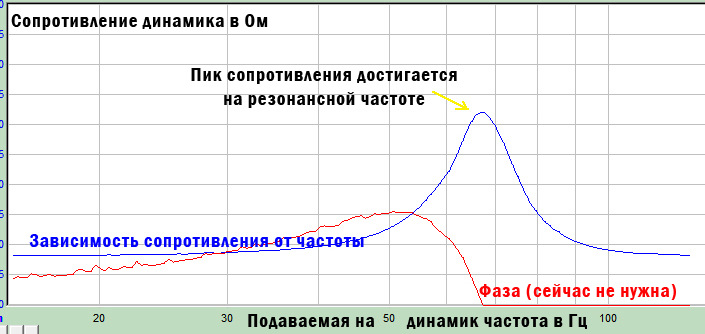
В документации к солидным динамикам всегда указывают эту величину, обозначается она Fs. Представляет собой некое значение частоты в герцах, при которой у динамика в свободном поле наблюдается резонанс. При замере динамик находится не в коробе (в идеале – на солидном удалении от любых отражающих поверхностей), он размят и замер делается при нормальной температуре. Легче всего этот резонанс определить по пику на графике зависимости сопротивления динамика от подаваемой на него частоты. Выглядит этот график примерно так:
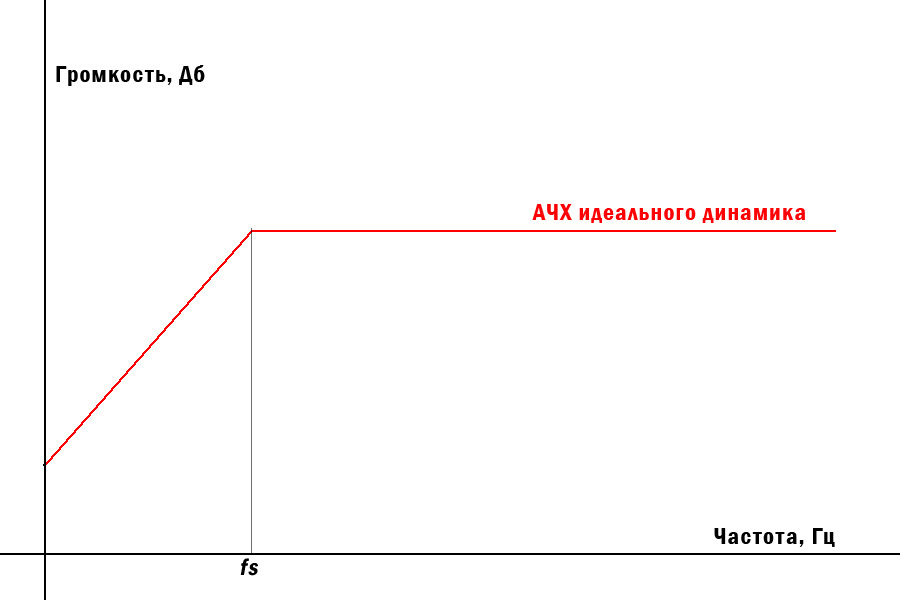
Завал начинается как раз на частоте резонанса. А после резонанса играет относительно ровненько до тех пор, пока ему позволяет его конструкция.
Проверил это утверждение на практике. Взял три динамика и снял АЧХ (микрофон в паре см от диффа) и их Т/С параметры. Выглядят динамики так:
Резонанс в физике для «чайников»
Мы часто слышим слово резонанс: «общественный резонанс», «событие, вызвавшее резонанс», «резонансная частота». Вполне привычные и обыденные фразы. Но можете ли вы точно сказать, что такое резонанс?
Если ответ отскочил у вас от зубов, мы вами по-настоящему гордимся! Ну а если тема «резонанс в физике» вызывает вопросы, то советуем прочесть нашу статью, где мы подробно, понятно и кратко расскажем о таком явлении как резонанс.
Прежде, чем говорить о резонансе, нужно разобраться с тем, что такое колебания и их частота.
Колебания и частота
Колебания – процесс изменения состояний системы, повторяющийся во времени и происходящий вокруг точки равновесия.
Резонанс может наступить только там, где есть колебания. И не важно, какие это колебания – колебания электрического напряжения, звуковые колебания, или просто механические колебания.
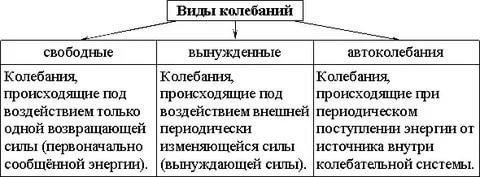
На рисунке ниже опишем, какими могут быть колебания.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Когда мы раскачиваем качели, периодически раскачивая систему с определенной силой (в данном случае качели – это колебательная система), она совершает вынужденные колебания. Увеличения амплитуды колебаний можно добиться, если воздействовать на эту систему определенным образом.
Толкая качели в определенный момент и с определенной периодичностью можно довольно сильно раскачать их, прилагая совсем немного усилий.Это и будет резонанс: частота наших воздействий совпадает с частотой колебаний качелей и амплитуда колебаний увеличивается.

Суть явления резонанса
Резонанс в физике – это частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы.
Суть явления резонанса в физике состоит в том, что амплитуда колебаний резко возрастает при совпадении частоты воздействия на систему с собственной частотой системы.

Примеры резонанса
Явление резонанса наблюдается в самых разных физических процессах. Например, звуковой резонанс. Возьмём гитару. Само по себе звучание струн гитары будет тихим и почти неслышным. Однако струны неспроста устанавливают над корпусом – резонатором. Попав внутрь корпуса, звук от колебаний струны усиливается, а тот, кто держит гитару, может почувствовать, как она начинает слегка «трястись», вибрировать от ударов по струнам. Иными словами, резонировать.
Действие микроволновки также основано на резонансе. В данном случае резонанс происходит в молекулах воды, которые поглощают излучение СВЧ (2,450 ГГц). Как следствие, молекулы входят в резонанс, колеблются сильнее, а температура пищи повышается.

Резонанс может быть как полезным, так и приносящим вред явлением. А прочтение статьи, как и помощь нашего студенческого сервиса в трудных учебных ситуациях, принесет вам только пользу. Если в ходе выполнения курсовой вам понадобится разобраться с физикой магнитного резонанса, можете смело обращаться в нашу компанию за быстрой и квалифицированной помощью.
Напоследок предлагаем посмотреть видео на тему «резонанс» и убедиться в том, что наука может быть увлекательной и интересной. Наш сервис поможет с любой работой: от реферата до курсовой по физике колебаний или эссе по литературе.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Про резонансную частоту, часть 1
Попробуем разобраться с ключевыми параметрами динамиков. Начнем с одного из самых основных параметров — с резонансной частоты(fs). Писал очень долго и муторно, сотни раз переделывал и переписывал, и получилось многабукафф:) Поэтому разбил на две части. Во второй части будет о том, как фс ведет себя при различных оформлениях и резонанс применительно к высокочастотникам.
От вас жду дополнений и исправлений! Попробуем вместе создать действительно хорошие тексты, доступно разъясняющие основы и физику звука. Надеюсь, не только мне хочется от и до во всем разобраться:) Текст не самый легкий, поэтому включаем думалку, и вперед:) Поехали!
Итак, резонансная частота. Разумеется, этот параметр не самодостаточный и для построения сколь угодно качественной системы знания одного его будет мало.
Динамик, как и любая колебательная система, имеет свою резонансную частоту. Это не незыблемая величина, она может довольно сильно меняться в зависимости от разных факторов. Например, температура упала => подвесы задубели – резонанс возрос. Закинули динамик в ЗЯ – резонанс возрос. Накидали на колпак сортирки с ПВА – резонанс упал.
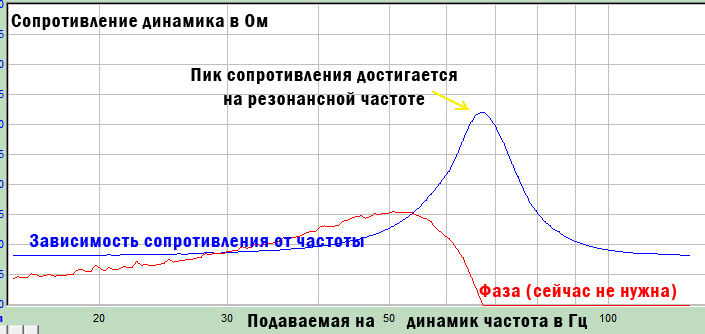
В документации к солидным динамикам всегда указывают эту величину, обозначается она Fs. Представляет собой некое значение частоты в герцах, при которой у динамика в свободном поле наблюдается резонанс. При замере динамик находится не в коробе (в идеале – на солидном удалении от любых отражающих поверхностей), он размят и замер делается при нормальной температуре. Легче всего этот резонанс определить по пику на графике зависимости сопротивления динамика от подаваемой на него частоты. Выглядит этот график примерно так:
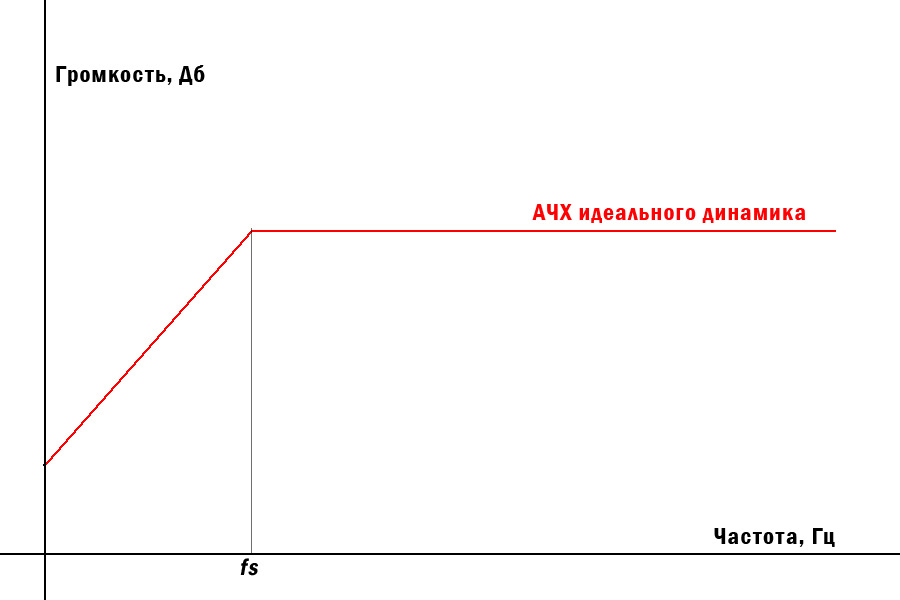
Завал начинается как раз на частоте резонанса. А после резонанса играет относительно ровненько до тех пор, пока ему позволяет его конструкция.
Проверил это утверждение на практике. Взял три динамика и снял АЧХ (микрофон в паре см от диффа) и их Т/С параметры. Выглядят динамики так:
Резонансная частота
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Содержание
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
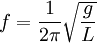
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
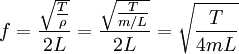
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Полезное
Смотреть что такое «Резонансная частота» в других словарях:
резонансная частота — Частота, на которой входной механический импеданс колебательной системы чисто активный и имеет минимальное значение. Единица измерения Гц [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения… … Справочник технического переводчика
резонансная частота — 257 резонансная частота Частота электрического тока и электрического напряжения при резонансе в электрической цепи Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа … Словарь-справочник терминов нормативно-технической документации
резонансная частота — rezonanso dažnis statusas T sritis automatika atitikmenys: angl. resonance frequency; resonant frequency vok. Resonanzfrequenz, f rus. резонансная частота, f pranc. fréquence de résonance, f … Automatikos terminų žodynas
резонансная частота — rezonanso dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Priverstinių virpesių dažnis, kuriam esant virpesių grandinėje įvyksta rezonansas. atitikmenys: angl. resonance frequency; resonant frequency vok. Resonanzfrequenz, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
резонансная частота — rezonanso dažnis statusas T sritis fizika atitikmenys: angl. resonance frequency; resonant frequency vok. Resonanzfrequenz, f rus. резонансная частота, f pranc. fréquence de résonance, f … Fizikos terminų žodynas
резонансная частота — Частота тока и напряжения при резонансе в цепи … Политехнический терминологический толковый словарь
резонансная частота — частота резонатора, при которой колеблющаяся величина достигает своего максимального значения … Русский индекс к Англо-русскому словарь по музыкальной терминологии
Резонансная частота — 1. Частота электрического тока и электрического напряжения при резонансе в электрической цепи Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь
резонансная частота — resonance frequency Частота вынужденных колебаний, при которой происходит резонанс. Шифр IFToMM: 3.9.35 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин
резонансная частота СВЧ защитного устройства — резонансная частота fрез Частота, при которой потери, вносимые СВЧ защитным устройством, имеют экстремальное значение. [ГОСТ 23769 79] Тематики приборы и устройства защитные СВЧ Обобщающие термины параметры СВЧ защитных устройств Синонимы… … Справочник технического переводчика
Резонансная частота: формула
Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Эффект резонанса
Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:
Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (
Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.
Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.
Определение колебательного контура
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Подключение к цепи индуктивной катушки
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На практике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.
Резонансная частота формула, которой имеет вид:
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Условие отсутствия резонанса
Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.
Амплитуда напряжения
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е — I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.
Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.