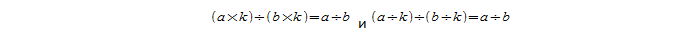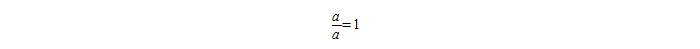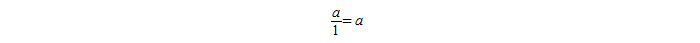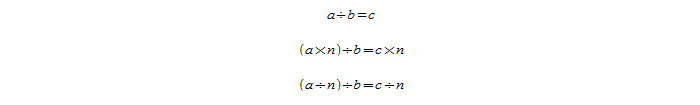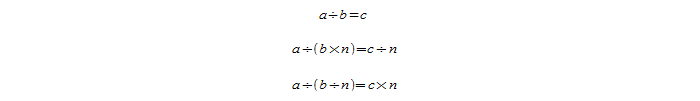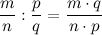Что такое частное чисел произведение чисел сумма чисел

Числовые и буквенные выражения

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

14 больше 4
14 > 4
6 + 8 > 2 * 2

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Пример 1. Найдите значение выражения: 5 + x.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Источник

Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.

Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.

Основное свойство частного

Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.

По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.

Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:

10 — 2 — 2 — 2 — 2 — 2 = 0.

Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:

Частное чисел – это итог процесса деления одного значения на второе. Пример:

Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:

При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:

Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:

Увеличение или уменьшение делимого

Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.

Изложенное правило имеет такой вид:

12 ⁄ 2 = 6 и пусть n = 3.

Проведём увеличение и уменьшение делимого:

То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.

Увеличение или уменьшение делителя

Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:

Для примера требуется взять частное двух значений 54 и 6:

a / b = c и пусть n = 3.

Проведём увеличение и уменьшение делителя:

Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.

Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.

Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.

Источник

Частное в математике — определение, свойства и формула

Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.

Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.

Основное свойство частного

Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.

По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.

Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:

10 — 2 — 2 — 2 — 2 — 2 = 0.

Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:

Частное чисел – это итог процесса деления одного значения на второе. Пример:

Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:

При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:

Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:

Увеличение или уменьшение делимого

Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.

Изложенное правило имеет такой вид:

12 ⁄ 2 = 6 и пусть n = 3.

Проведём увеличение и уменьшение делимого:

(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;

(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.

То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.

Увеличение или уменьшение делителя

Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:

Для примера требуется взять частное двух значений 54 и 6:

a / b = c и пусть n = 3.

Проведём увеличение и уменьшение делителя:

54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;

54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.

Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.

Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.

Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.

Источник

Что такое частное чисел произведение чисел сумма чисел

Что такое частное чисел (онлайн калькулятор на деление)

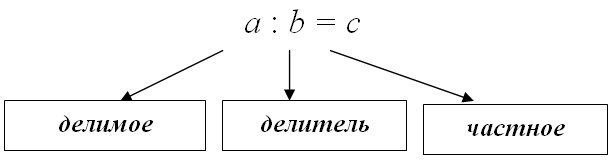
Определение частного чисел (деление)

Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.

Как делить столбиком (о правилах деления столбиком)

4. Если в конце таких вычислений получается число которое невозможно поделить на делитель и сносить уже нечего, то это было деление с остатком. То есть оставшееся число или цифра, это остаток. Надо понимать, что остаток всегда должен быть меньше делителя. В этом вся соль остатка, он не позволяет взять из себя делитель даже одного раза!

Деление рациональных дробей

Для деления дробей используется следующее правило.

То есть если сказать без глубоких объяснений процессов происходящего, берем дробь, где в числителе произведение числителя делимого и знаменателя делителя, а в знаменателе этой дроби произведение знаменателя делимого и числителя делителя!

Что же, я думаю вы уже утомились воспринимать информацию и теперь вам лучше всего развеяться, поиграв с онлайн калькулятором на деление. А и тут сразу же в голове всплыло еще одно правило, на ноль делить нельзя, так как даже в самом маленьком числе нулей великое множество, то есть бесконечность, а наш курс все же для школьников начальных и средних классов, где о бесконечности знают лишь то, что можно бесконечно играть в компьютер и не более:) А как на деление с нолем отреагирует калькулятор, можете проверить сами.

Побалуемся с делением!?

Цифра которую будем делить (делимое)

Источник

Основные арифметические действия: определения, примеры

В данной публикации мы рассмотрим определения, общие формулы и примеры 4 основных арифметических (математических) действий с числами: сложения, вычитания, умножения и деления.

Сложение

Сложение – это математическое действие, в результате которого находится сумма.

Обозначается сложение специальным знаком “+“ (плюс), а сумма – “Σ“.

Пример: найдем сумму чисел.
1) 3, 5 и 23.
2) 12, 25, 30, 44.

Ответы:
1) 3 + 5 + 23 = 31
2) 12 + 25 + 30 + 44 = 111.

Вычитание

Вычитание чисел – это обратное сложению математическое действие, в результате коротого находится разность ( c ). Например:

Обозначается вычитание специальным знаком “–“ (минус).

Пример: найдем разность чисел.
1) 62 минус 32 и 14.
2) 100 минус 49, 21 и 6.

Ответы:
1) 62 – 32 – 14 = 16.
2) 100 – 49 – 21 – 6 = 24.

Умножение

Умножение – это арифметическое действие, в результате которого вычисляется произведение.

Обозначается умножение специальными знаками “·“ или “x“.

Пример: найдем произведение чисел.
1) 3, 10 и 12.
2) 7, 1, 9 и 15.

Ответы:
1) 3 · 10 · 12 = 360.
2) 7 · 1 · 9 · 15 = 945.

Деление

Деление чисел – это обратное умножению действие, в результате коротого вычисляется частное ( d ). Например:

Обозначается деление специальными знаками “:“ или “/“.

Пример: найдем частное чисел.
1) 56 разделим на 8.
2) 100 разделим на 5, затем на 2.

Ответы:
1) 56 : 8 = 7.
2) 100 : 5 : 2 = 10 (, ).

Источник