Что такое частичный предел

Частичный предел последовательности

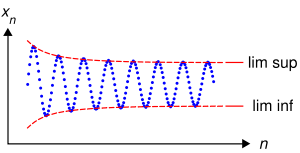
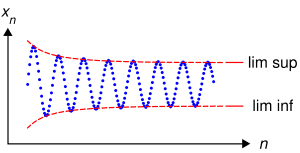
Частичный предел некоторой последовательности — это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательностей частичный предел совпадает с обычным пределом в силу единственности последнего, однако в самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.

Два важных частных случая частичного предела — верхний и нижний пределы.

Содержание

Определение

Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. В некоторой литературе в случаях, если из последовательности удаётся выделить бесконечно большую подпоследовательность, все элементы которой одновременно положительны или отрицательны, её частичным пределом называют соответственно или .

Нижний предел последовательности — это точная нижняя грань множества частичных пределов последовательности.

Верхний предел последовательности — это точная верхняя грань множества частичных пределов последовательности.

Иногда нижним пределом последовательности называют наименьшую из её предельных точек, а верхним — наибольшую. [1] Очевидно, что эти определения эквивалентны.

Обозначения

Нижний предел последовательности :

Верхний предел последовательности :

Примеры

Свойства

Примечания

Полезное

Смотреть что такое «Частичный предел последовательности» в других словарях:

Частичный предел — Верхний предел (lim sup) и нижний предел (lim inf) последовательности. Частичным пределом последовательности называется предел какой либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. Очевидно, что… … Википедия

ЧАСТИЧНЫЙ ПРЕДЕЛ — данной последовательности предел нек рой ее подпоследовательности. У всяком числовой последовательности (а также у всякой последовательности точек конечномерного евклидова пространства) существует, по крайней мере, один Ч. п. (конечный или… … Математическая энциклопедия

Предел числовой последовательности — Предел числовой последовательности предел последовательности элементов числового пространства. Числовое пространство это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел … Википедия

Предел — объект, представляющий собой воображаемую или реальную границу для другого объекта. В математическом анализе см. Предел (математика), а также: Предел последовательности Предел функции Предел категории Частичный предел Проективный предел Банаховы… … Википедия

ПРЕДЕЛ — одно из основных понятий математики, означающее, что какая то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек рому постоянному значению. Основным при определении П. является… … Математическая энциклопедия

Предел (математика) — У этого термина существуют и другие значения, см. Предел. Предел одно из основных понятий математического анализа. Различают предел последовательности и предел функции. Понятие предела на интуитивном уровне использовалось ещё во второй половине… … Википедия

Предел — одно из основных понятий математики. П. постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой … Большая советская энциклопедия

Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия

Асимптотическая плотность — В теории чисел асимптотическая плотность это одна из характеристик, помогающих оценить, насколько велико подмножество множества натуральных чисел … Википедия

Источник

ЧАСТИЧНЫЙ ПРЕДЕЛ

Смотреть что такое «ЧАСТИЧНЫЙ ПРЕДЕЛ» в других словарях:

Частичный предел — Верхний предел (lim sup) и нижний предел (lim inf) последовательности. Частичным пределом последовательности называется предел какой либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. Очевидно, что… … Википедия

Частичный предел последовательности — Верхний предел (lim sup) и нижний предел (lim inf) последовательности. Частичный предел некоторой последовательности это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательн … Википедия

Предел числовой последовательности — Предел числовой последовательности предел последовательности элементов числового пространства. Числовое пространство это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел … Википедия

Предел — объект, представляющий собой воображаемую или реальную границу для другого объекта. В математическом анализе см. Предел (математика), а также: Предел последовательности Предел функции Предел категории Частичный предел Проективный предел Банаховы… … Википедия

Предел (математика) — У этого термина существуют и другие значения, см. Предел. Предел одно из основных понятий математического анализа. Различают предел последовательности и предел функции. Понятие предела на интуитивном уровне использовалось ещё во второй половине… … Википедия

ПРЕДЕЛ — одно из основных понятий математики, означающее, что какая то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек рому постоянному значению. Основным при определении П. является… … Математическая энциклопедия

Предел — одно из основных понятий математики. П. постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой … Большая советская энциклопедия

Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия

Асимптотическая плотность — В теории чисел асимптотическая плотность это одна из характеристик, помогающих оценить, насколько велико подмножество множества натуральных чисел … Википедия

Источник

Частичный предел

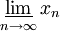
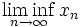
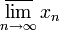
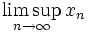
Нижним пределом последовательности (обозначается или ) называется наименьший элемент множества частичных пределов последовательности, а верхним пределом ( или ) — наибольший элемент.

Докажем это утверждение для верхнего предела. По теореме Больцано — Вейерштрасса множество частичных пределов ограниченной последовательности непусто. Пусть s — верхняя грань множества A частичных пределов. Тогда заметим, что 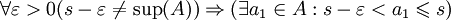, а это означает, что в любой окрестности точки a₁ находится бесконечно много членов последовательности. Поскольку утверждение верно для любого , мы можем сказать, что в любой окрестности точки s содержится бесконечно много членов последовательности (так как в любой окрестности мы можем найти точку a₁ ). Значит, s по определению является предельной точкой последовательности, а стало быть, и её частичным пределом, что и требовалось доказать. Аналогично доказывается случай нижнего предела.

Последовательность <x_n> сходится к a тогда и только тогда, когда 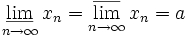, так как получается, что a — единственная предельная точка множества элементов последовательности.

Полезное

Смотреть что такое «Частичный предел» в других словарях:

ЧАСТИЧНЫЙ ПРЕДЕЛ — данной последовательности предел нек рой ее подпоследовательности. У всяком числовой последовательности (а также у всякой последовательности точек конечномерного евклидова пространства) существует, по крайней мере, один Ч. п. (конечный или… … Математическая энциклопедия

Частичный предел последовательности — Верхний предел (lim sup) и нижний предел (lim inf) последовательности. Частичный предел некоторой последовательности это предел одной из её подпоследовательностей, если только он существует. Для сходящихся числовых последовательн … Википедия

Предел числовой последовательности — Предел числовой последовательности предел последовательности элементов числового пространства. Числовое пространство это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел … Википедия

Предел — объект, представляющий собой воображаемую или реальную границу для другого объекта. В математическом анализе см. Предел (математика), а также: Предел последовательности Предел функции Предел категории Частичный предел Проективный предел Банаховы… … Википедия

Предел (математика) — У этого термина существуют и другие значения, см. Предел. Предел одно из основных понятий математического анализа. Различают предел последовательности и предел функции. Понятие предела на интуитивном уровне использовалось ещё во второй половине… … Википедия

ПРЕДЕЛ — одно из основных понятий математики, означающее, что какая то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек рому постоянному значению. Основным при определении П. является… … Математическая энциклопедия

Предел — одно из основных понятий математики. П. постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой … Большая советская энциклопедия

Числовая последовательность — Последовательность Числовая последовательность это последовательность элементов числового пространства. Числовые пос … Википедия

Асимптотическая плотность — В теории чисел асимптотическая плотность это одна из характеристик, помогающих оценить, насколько велико подмножество множества натуральных чисел … Википедия

Источник

Подпоследовательности. Частичные пределы.

Подпоследовательность.

Пусть задана последовательность \(\\>\). Рассмотрим строго возрастающую последовательность \(\\) натуральных чисел, то есть такую, что
$$
n_ <1>Теорема.

Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

\(\circ\) Пусть \(\\>\) — ограниченная последовательность, тогда все члены последовательности принадлежат некоторому отрезку, то есть
$$
\exists a, \ b:\forall n\in\mathbb\rightarrow x_\in\Delta=[a, \ b].\label
$$

Разобьем отрезок \(\Delta=[a, \ b]\) пополам точкой d. Тогда по крайней мере один из отрезков \([a, \ d], \ [d, \ b]\) содержит бесконечное число членов последовательности \(\\>\). Если оба отрезка обладают этим свойством, возьмем, например, правый отрезок (и будем так поступать в дальнейшем). Выбранный отрезок, содержащий бесконечное число членов данной последовательности, обозначим \(\Delta_1=[a_<1>, \ b_<1>]\), его длина равна
$$
b_<1>-a_<1>=\frac<2>.\nonumber
$$

Разделив отрезок \(\Delta_<1>\) пополам, выберем указанным выше способом из двух получившихся отрезков отрезок \(\Delta_<2>=[a_<2>,b_<2>]\), содержащий бесконечное число членов последовательности \(\\>\).

Продолжая эти рассуждения, получим последовательность \(\<\Delta_n=[a_n, \ b_n]\>\) отрезков таких, что:

Следовательно, \(\Delta_n\) — стягивающаяся последовательность отрезков. По теореме Кантора существует единственная точка c, принадлежащая всем отрезкам, то есть
$$
\exists c:\forall k\in\mathbb\rightarrow c\in\Delta_.\label
$$

Покажем, что найдется подпоследовательность \(\>\>\) последовательности \(\\>\) такая, что
$$
\lim_x_>=c.\label
$$

Так как отрезок \(\Delta_<1>\) содержит бесконечное число членов последовательности \(\\), то
$$
\exists n_<1>\in\mathbb:x_>\in\Delta_<1>.\nonumber
$$

Отрезок \(\Delta_<2>\) также содержит бесконечное число членов данной последовательности, и поэтому
$$
\exists n_2>n_1: x_\in\Delta_2.\nonumber
$$
Вообще, можно записать, что
$$
\forall k\in\mathbb\quad\exists n_k: \ x_\in\Delta_k, \ где \ n_1 Замечание.

Теорему Больцано-Вейерштрасса можно сформулировать так: любая ограниченная последовательность имеет хотя бы один частичный предел.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

2. Предел последовательности

Последовательность

Таким образом, числовая последовательность это частный вид функции, в котором элементу из множества натуральных чисел по определенному закону однозначно ставится в соответствие элемент из множества вещественных чисел.

Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.

Пример. Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел. Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.

Определение. Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.

Определение. Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

Ограниченная последовательность — это последовательность, ограниченная и сверху, и снизу.

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.

Предел последовательности

\exists N(\varepsilon )\in \mathbb \colon

\exists N(E)\in \mathbb \colon

\forall n\geqslant N\Rightarrow |x_|>E$$

Любая последовательность, стремящаяся к бесконечности — неограниченная. Однако обратное неверно.

В самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.

Верхний (lim sup) и нижний пределы (lim inf):

Свойства

Сумма, разность, произведение сходящихся последовательностей также является сходящейся последовательностью. [Частное не всегда]

Взятие предела числовой последовательности является линейным:

Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

Единственность. Сходящаяся числовая последовательность имеет только один предел. Доказательство: Тер-Крикоров, с.40.

Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.

У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.

Предел средних арифметических, геометрических

Тем самым, операция взятия среднего обладает свойством регулярности — сохраняет свойство сходимости последовательности и её предел.

Аналогично для последовательности средних геометрических, доказательство

Предельный переход в неравенствах

Доказательство от противного, по определению предела.

Предельный переход сохраняет знак нестрогого неравенства. Однако знак строгого неравенства, вообще говоря, не сохраняется.

Теорема о двух милиционерах

Справедлива теорема о двух милиционерах (теорема сжатия)

\forall n\geqslant N\colon x_\leqslant z_\leqslant y_

Бесконечно малые

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности. [если для любого вещественного числа все члены последовательности, начиная с некоторого, оказываются по модулю больше этого числа. ]

Сумма, разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Любая бесконечно малая последовательность ограничена.

Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

Предельная точка последовательности

Определение. Назовем точку x предельной точкой множества E, если в произвольной окрестности точки x существует хотя бы одна точка из E, отличная от x.

Сама точка x может принадлежать, а может и не принадлежать множеству E.

$$\forall \varepsilon > 0 \, \exists y, y \ne x : \, |x-y| 0

\exists X\subseteq \mathbb \colon \left|X\right|=\aleph _<0>\land \forall i\in X\colon \left|x_-x\right| 0

\exists x \in X\colon \, 0 0$ с центром в x нет ни одной точки из E, отличной от x, а это невозможно, поскольку x – предельная точка множества E.

Теорема. Точка является предельной точкой последовательности тогда и только тогда, когда из этой последовательности можно выделить подпоследовательность, сходящуюся к этой точке.

Задача. Доказать, что если последовательность сходится к a (то есть a является ее пределом), то она не имеет предельных точек, отличных от a.

т.е. Всякая сходящаяся числовая последовательность имеет только одну предельную точку.

Для сходящихся числовых последовательностей предельная точка совпадает с пределом.

У произвольной числовой последовательности имеется хотя бы одна предельная точка (либо вещественная, либо бесконечность).

Пример. У последовательности из всех рациональных чисел, занумерованных произвольным образом, существует бесконечно много предельных точек.

Примеры

Фундаментальная последовательность

Определение. Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии менее, чем заданное.

Определение. Фундаментальная последовательность — это последовательность элементов метрического пространства, в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного.

Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.

Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).

Определение. Пространство, в котором каждая фундаментальная последовательность сходится к элементу этого же пространства, называется полным.

Каждая сходящаяся последовательность является фундаментальной, но не каждая фундаментальная последовательность сходится к элементу из своего пространства.

Метрическое пространство является полным тогда и только тогда, когда всякая система вложенных замкнутых шаров с неограниченно убывающим радиусом имеет непустое пересечение, состоящее из одной точки.

Теорема Больцано — Вейерштрасса

Теорема. Если последовательность имеет предел, то она ограничена. [очевидно. например, взять ε=1]

Ограниченная последовательность имеет по крайней мере одну предельную точку.

Теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Источник